d라이브러리

마음에는 안 들지만 견우 녀석이 잘 하는지 신경쓰여서 지켜보게 되네요. 앗, 그런데 사각지대로 들어간 건지 견우가 사라졌어요! 알고리듬도 모르는 사람이 CCTV를 설치했나봐요.

CCTV는 보안이 필요한 곳에 설치하는 감시용 장치예요. 사각지대가 생기지 않게 효율적으로 CCTV를 설치하려면 ‘집합 덮개 문제’를 푸는 알고리듬을 활용하면 돼요.
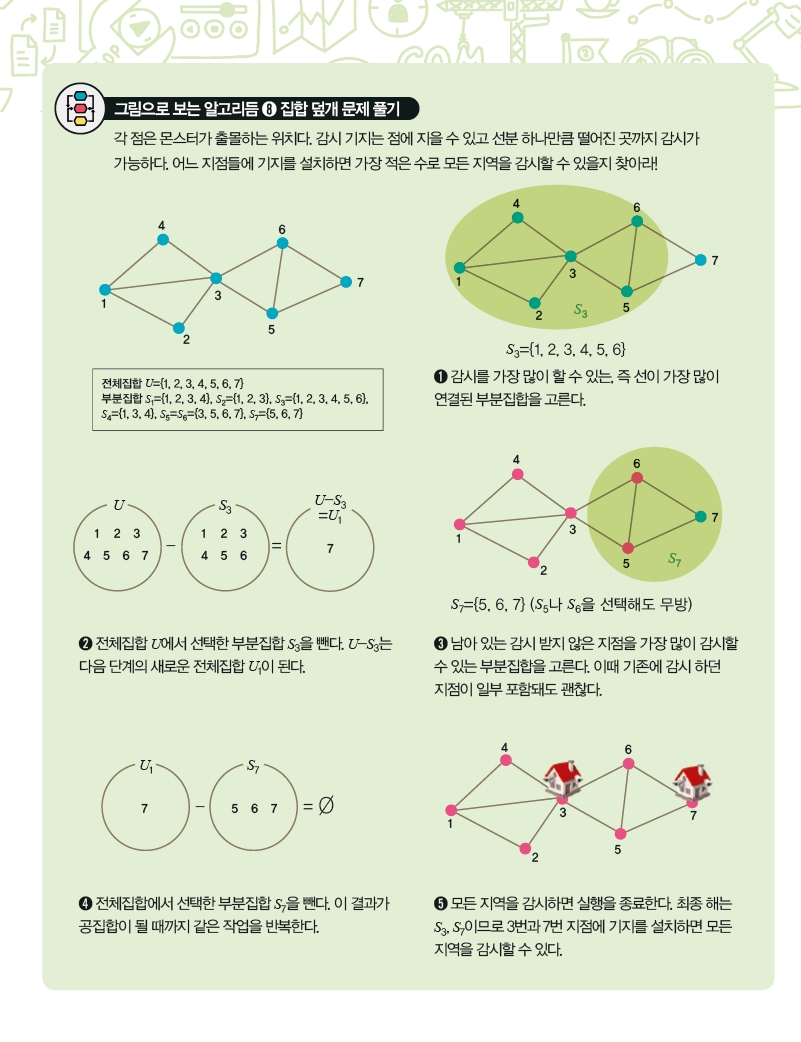
집합 덮개 문제는 n개의 원소를 가진 전체집합 U가 있을 때, U의 부분집합들을 어떻게 선택하면 최소 집합으로 전체집합 U를 덮을 수 있는지 알아내는 문제예요. 
아래 그림에서 각 점은 ‘세이브스쿨’ 속 몬스터들이 출몰하는 위치예요. 그리고 점들을 연결한 선분은 각 점에 감시 기지를 지었을 때 감시할 수 있는 거리를 나타낸다고 할게요. 기지는 선분 1개까지 떨어진 곳만 감시할 수 있어요. 예를 들어 4번에 기지를 지으면 2번이나 8번, 3번 위치는 보이지만 1번이나 6번은 볼 수 없어요. 

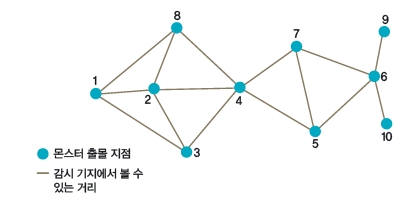
이때 전체집합 U는 1번부터 10번까지 모든 지점을 포함하는 집합 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}이고, 부분집합 Si은 i 지점에 기지를 지었다고 할 때 볼 수 있는 지점으로 각각 S₁={1, 2, 3, 8}, S₂={1, 2, 3, 4, 8}, S₃={1, 2, 3, 4},…, S₁₀={6, 10}이죠. 부분집합을 모두 찾았다면 이제 어느 위치에 기지를 지으면 가장 적은 개수로 전체를 감시할 수 있는지 생각해 보세요. 선택한 부분집합 S_i들의 합집합이 전체집합이 되면 된답니다.
찾았나요? 정답은 2번과 6번 자리예요. S₂={1, 2, 3, 4, 8}, S₆={5, 6, 7, 9, 10}를 고르면 기지를 2개만 지어서 모든 몬스터 출몰지를 감시할 수 있지요. 이렇게 점이 조금만 있을 때는 일일이 부분집합의 조합을 따져보면 정확한 답을 찾을 수 있어요. 하지만 원소의 수 n이 아주 큰 전체집합일 때는 부분집합의 조합이 2ⁿ-1개이므로 전부 따져보기가 무척 어려워져요. 이 문제는 NP-완전으로 밝혀져 실제로 생활에 쓰일 때는 근사알고리듬으로 최적해에 가까운 답을 찾아서 쓰고 있어요. 그럼 모든 조합을 따지지 않고 근사해를 찾는 방법을 알려드릴게요!