d라이브러리

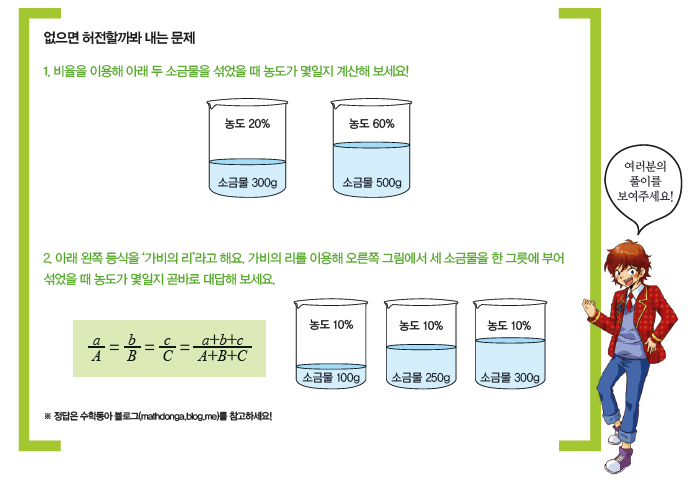
키 크고 얼굴이 조막만 한 사람을 ‘팔등신’, ‘1:8의 비율’이라고 하죠. 정확히 말하면 1:8은 ‘비’고 이걸 분수로 나타낸 게 ‘비율’이라는 거수학동아TV 시청자라면 알고 있었겠죠? 비든 비율이든 BJ맹추는 팔등신과 거리가 멀지 않냐고요? 음…. 어서 방송 시작합시다.

기준 없이 못사는 비와 비율

자, 모두 눈을 감으세요. 몸은 공중에 떠있고 주변은 온통 하얗습니다. 이제 머릿속으로 친구에게 내 위치를 설명해보세요. 별거 아닌 것 같아도 아마 쉽지 않을 겁니다. 이유가 뭘까요? 보통 위치를 설명할 때 ‘◯ ◯ 왼쪽에 있다’, ‘◯ ◯에서 몇 미터 떨어져 있어’라고 표현하는데, ‘왼쪽’이나 ‘떨어 져 있다’는 모두 ◯ ◯라는 ‘기준’이 있어야 쓸 수 있기 때문이에요.

마찬가지로 비와 비율도 기준이 있어야 합니다. 기준이 되는 양에 비해 비교하는 양이 얼마나 있는지 한 번에 나타내는 게 비 또는 비율이니까요. ‘팔등신’은 얼굴 길이와 키의 비가 1:8이라는 말입니다. 머리끝부터 발끝까지를 8등분했을 때 얼굴은 1만큼 차지한다는 뜻이지요.

팔등신에서 키를 나타내는 8이 기준이었던 것처럼, ‘:’ 뒤에 있는 수가 기준이 되는 양이고 앞에 있는 수가 비교하는 양입니다. 비율은 비교하는 양을 분자, 기준이 되는 양을 분모에 써서 분수(18)로 나타낸 거지요.

키가 커야 팔등신?

보통 키 크고, 얼굴도 작은 연예인을 팔등신이라고 하니까 키가 커야만 팔등신이 될 수 있다고 착각하는 사람이 있어요. 만약 그랬다면, 비를 좀 더 확실히 이해할 필요가 있습니다!

비는 비교하는 양이 기준이 되는 양에 비해 ‘어느 정도를 차지하고 있는지’를 상대적으로 나타내는 것으로, 실제 크기나 길이는 상관없습니다. 콩 반 조각과 수박 반 조각 중 수박 조각이 훨씬 크지만 전체를 기준으로 보면 둘 다 비가 1:2이지요.

이번엔 비율로 써볼까요? 콩의 무게가 4g이고 수박은 800g이라고 칩시다. 콩 반 조각은 2g이니까 전체와 비율을 따져보면 2/4고, 수박 800g 중 절반은 400g이니까 비율은 400/800이지요. 기약 분수로 나타내면 2/4나 400/800 모두 1/2이니까 둘 다 비율은 똑같은 겁니다.

비슷하게 팔등신은 얼굴 길이와 키의 비가 1:8이면 되니까 키가 176cm인 사람은 얼굴 길이가 22cm면 되고 160cm인 사람은 20cm면 됩니다. 키가 작아도 얼마든지 팔등신이 될 수 있는 거지요. 물론, 얼굴도 그만큼 작아야 하는 건 함정이지만요!

막강한 비례식

비를 비율로 바꿔 보면 재밌는 규칙을 찾을 수 있어요. 1/2=2/4=3/6=…처럼 크기는 같고 분모, 분자가 다른 분수를 살펴보면 이 분수 중에 어떤 두 개를 골라도 두 분수의 분모와 분자를 엇갈려 곱한 값은 항상 같습니다.

를 들어 1/2과 2/4을 골라 엇갈려 곱하면 1×4=2×2가 되고, 1/2과 3/6은 1×6=2×3인 것처럼요. 이제 이 분수를 비로 바꿔 볼게요.

앞에 나온 분수를 비로 나타내면 1:2, 2:4,3:6,…입니다. 앞에서 고른 것처럼 1:2와 2:4를 골라 1/2=2/4를 1:2=2:4 같은 ‘비례식’으로 써봅시다. 아까 엇갈려 곱한 값이 비례식에서 어디에 있는지 찾아보면 1과 4는 바깥쪽에, 2와 2는 등호양 옆에 있습니다. 그러면 아래 공식을 얻을 수 있지요.

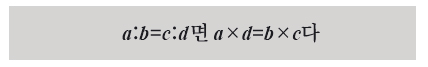
팔등신인 사람의 키만 알면 이 공식으로 얼굴 길이도 쉽게 알아낼 수 있습니다. 별거 아닌 것 같아도 그리스 수학자 탈레스와 에라토스테네스는 이 공식을 써서 거대한 피라미드의 높이와 지구의 반지름을 알아냈으니 정말 강력하죠?

그만 좀 섞어!

수학의 묘미는 바로 아~주 복잡한 문제를 간단하게 푸는 겁니다. 실제로 수학자는 똑같은 증명이라도 길고 복잡한 것보다 간단하고 짧은 증명을 더 좋아하거든요. 마침 이번 개념이 비와 비율이니까, 비와 비율을 이용해 수학의 묘미를 느껴볼까요?

BJ맹추가 중학생 때 가장 싫어한 수학 문제가 농도가 다른 소금물을 섞으면 농도가 어떻게 바뀌는지 묻는 문제입니다. 농도는 소금물의 양을 기준으로 소금이 얼마나 들어있는지 나타내는 비율로, 소금의 양/소금물의 양 ×100으로 구할 수 있어요. 100을 곱하는 이유는 비율을 백분율로 나타내기 위한 것이니 잠깐 제쳐 둡시다.

문제는 ‘농도가 10%인 소금물 300g과 4%인 소금물 100g을 섞으면 농도가 얼마일까요?’라는 식입니다. 복잡하지요. 소금물 400g이 되는 건 당연한데, 그 안에 소금이 얼마나 들어있는지 알아내려면 두 소금물을 섞기 전에 각 소금물에 들어있는 소금을 따로 구해서 더해야 하니까요.

소금물의 시소 타기

자, 여기서 직관을 발휘해 봅시다! 만약 소금물의 양은 같고 농도가 다른 두 소금물을 섞으면 어떻게 될까요? 무게가 같은 두 사람이 시소를 타면 시소의 축이 정확히 중간에 있을 때 평형을 이루는 것처럼 두 농도의 딱 중간 값이 농도가 됩니다.

반면 시소에 탄 두 사람의 무게가 다르면 무거운 사람 쪽으로 기울어집니다. 이걸 평형이 되게 하려면 시소의 축을 무거운 사람 쪽으로 옮겨야 하지요. 소금물도 마찬가지입니다. 소금물의 양이 다르면, 축의 위치도 한쪽으로 치우치지요.

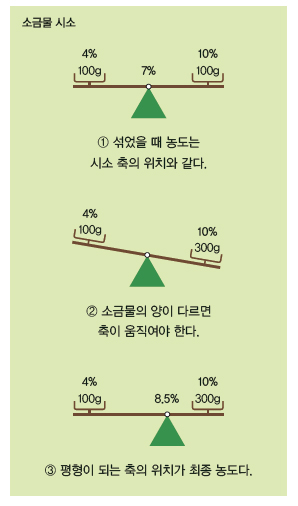
축이 정확히 얼마나 치우치냐는 전체 소금물의 양을 기준으로 각 소금물 양의 비율에 의해 결정됩니다. 위 문제에서 소금물 100g과 300g의 비율은 각각 100/400 , 300/400 입니다. 이 값을 각 농도에 곱해 더하면 정확히 섞었을 때 농도가 됩니다. 즉, 두 소금물을 섞으면 농도는 4×1/4+10×3/4
=8.5%가 되는 거예요.

이렇게 비율을 이용하면 소금의 양을 따로 구하지 않아도 곧바로 농도를 구할 수 있습니다. 오히려 이해하기 어렵다고요? 그럴까봐 시소 그림과 문제를 준비했으니 곰곰이 생각해 보세요. 소금의 양을 따로 구해서 농도를 구했을 때와 비교해 보면 더 좋겠죠?

비, 비, 비자로 끝나는 말

비와 비율은 도형을 공부할 때도 자주 등장합니다. 어떤 두 도형이 ‘닮았다’를 바꿔 말하면 두 도형의 같은 위치에 있는 변의 길이의 비가 모두 같다는 뜻이고, 수학에서 매우 중요한 ‘삼각비’는 직각삼각형의 세 변 중 두 변의 비율을 나타내는 개념이지요.

다시 강조하지만, 비율은 값보다 기준이 되는 양에 비해 얼마나 있는지가 핵심입니다. 헷갈리면 몸속 지방의 양이 같아도 몸집이 크면 적정 체중이고 작으면 비만일 수 있다는 걸 떠올리세요.

자, 비율을 잘~ 쓰길 바라면서, 이만 방송을 마치겠습니다. 그럼 안녕~. 뿅!