d라이브러리

퍼즐을 이해하고 여러 가지 아이디어를 떠올려 해결하는 것 모두 뇌에서 담당하는 거잖아. 그래서 말인데, 수학퍼즐을 풀 때 우리 뇌에선 어떤 반응이 일어날까? 또 영재들의 뇌는 뭔가 다르지 않을까? 뇌에 대한 비밀을 밝혀 줘~.

지능은 두 가지로 나뉘어. 나이가 들어 감에 따라 유지되거나 높아지는 결정적 지능과 성장과 함께 높아지다가 성장이 멈추면 점차 떨어지는 유동성 지능이지. 그런데 베르니케 영역처럼 언어를 담당하는 기관은 결정적 지능과 관련이 있고 전전두엽이나 후두정엽처럼 기발한 발상이나 추론능력을 담당하는 기관은 유동성 지능과 관련이 깊대. 소설가는 지긋한 나이에도 왕성한 활동을 하지만 연로한 컴퓨터 프로그래머는 찾아보기 어려운 이유가 이 때문이래. 그런데 청소년기 이후에는 발달하지 않는 유동성 지능을 발달시키는데는 수학퍼즐이 최고야. 따라서 수학퍼즐을 열심히 즐겨야 하지! 시간이 없거든.

영재성 검사에  퍼즐 나오는 이유

수학·과학 영재프로그램에 빠지지 않는 것이 수학퍼즐이야. 그리고 영재성 검사를 받아 본 친구들은알겠지만 수리 또는 공간 영역에 수학퍼즐로 보이는 문제들이 출제되지. 왜 그런 걸까?

어떤 문제에 꽂히면 그 문제를 해결할 때까지 매달리는 능력(과제집착력), 뛰어난 수학·과학 성적을 거두는 능력(문제해결력), 톡톡 튀는 아이디어를 술술 내놓는 능력(창의력). 이 모든 능력을 갖춘 친구를 우리는 수학영재라고 부르지. 이런 영재를 발굴하기 위해 다양한 검사방법이 존재해. 사실 어떤시험 하나로 ‘넌 이제부터 수학영재야’ 라고 말하는 게 웃기잖아. 그래서 담당 학생을 가르쳤던 교사의 추천, 영재성 검사, 면담을 통해 영재를 판별해내.

영재성 검사는 언어, 수리, 공간지각, 창의력에 대해 보통 이상의 지적능력을 갖췄는지 판별하는 검사야. 그런데 어디에서도 보지 못한 특이한 문제를 출제하다 보니 수리, 공간지각, 창의력 영역에서 수학퍼즐이 출제되는 거야. 학생들이 많이 접한 유형의 문제를 제공하면 너도나도 문제를 잘 해결하기 때문에 영재를 판별해낼 수 없으니까.

이렇게 선발된 영재들에게 수학퍼즐을 풀게 하는 이유는 수학퍼즐 안에 수학 원리가 숨겨져 있기 때문이야. 또 퍼즐은 영재가 갖춰야 할 능력인 과제집착력, 문제해결력, 창의력을 향상시키기 때문이지.

영재는 퍼즐 풀고 수학 원리도 발견

보통 퍼즐을 풀 때 우리는 답을 구하기 위해 노력하잖아. 하지만 수학영재들은 이 속에서 수학적 원리를 발견하는 데 열중한대. 믿기지 않는다고? 예를 들어 설명해 줄게.

다음은 어떤 건물의 건축도면이야. 모든 벽에는 반드시 문이 하나씩 있다고 할 때 모든 문을 한 번씩 지나갈 수 있는 도면은 어떤 걸까? 도면 안의 숫자는 벽면의 개수야(단, 한 번 사용한 문은 다시 지날 수 없지).
 

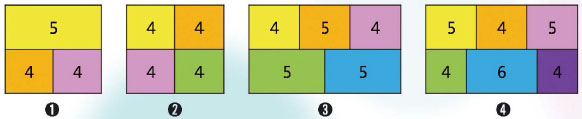
다음과 같은 수학퍼즐을 푼다고 할 때 우리는 여러 가지 경우를 따져 가며 답안을 찾는 것에만 열중할 거야. 답안을 찾고 나면 퍼즐을 풀었다는 만족감을 느낀 채 손을 떼지. 그런데 수학영재들은 답안을 찾고 그 답을 통해서 어떤 규칙성을 발견한대. 수학영재인 김진원 군의 풀이를 살펴볼게.

김진원 군의 풀이
 

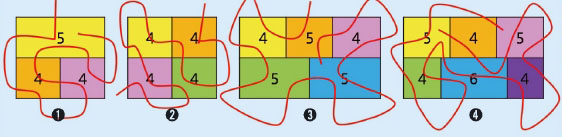
정답은 ➊, ➋, ➍다.
벽면의 수가 홀수 개인 방의 개수가 두 개 이하일 때만 모든 문을 지날 수 있다. ➊처럼 벽면의 개수가 홀수 개인 방의 개수가 한 개일 때는 그 방의 내부에서 시작해 그 방의 외부에서 끝나는 회로를 구할 수 있다. ➋처럼 벽면의 수가 짝수로만 돼 있을 때는 어느 방에서 시작하더라도 모든 문을 지나는 회로를 그릴 수 있다. ➍처럼 벽면의 수가 홀수 개인 방이 두 개일 때는 벽면의 수가 홀수 개인 방에서 시작해 벽면 수가 홀수 개인 다른 방에서 끝나는 회로를 찾을 수 있다.
 

진원 군의 풀이가 어때? 놀라 입이 딱 벌어지지. 이런 활동은 수학영재에게 수학적 호기심과 새로운 발견에 대한 기쁨을 준대.

수학영재들이 수학퍼즐을 푸는 이유를 이제 알겠지? 우리가 흔히 푸는 스도쿠도 수학 영재들의 손에 들어가면 다른 문제로 탈바꿈해. 스도쿠는 몇 가지나 가능한지 등을 궁리하지. 믿기지 않는다고?

이를 증명한 수학영재가 있어. 독일 드레스덴기술대학의 버트람 펠겐하우어와 영국 셰필드대학의 프레이저 야비스는 가로·세로가 각각 9칸인 스도쿠의 경우의 수를 구했어. 무 6670903752021072936960라고 해. 스도쿠에 푹 빠진 친구들에겐 희소식이지. 평생 다른 스도쿠를 풀 수 있겠어. 그런데 이 숫자는 답이 여러 개인 스도쿠까지 포함된 거야.

스도쿠를 좋아하는 친구들은 스도쿠의 수학에 도전해 봐. 새로운 발견으로 언젠가 신문에 이름이 대문짝만 하게 실릴지도 모르잖아!

tip 스도쿠를 만든 세 남자

스도쿠 하면 가장 먼저 떠오르는 이름이 스위스의 수학자 레온하르트 오일러야. 스도쿠의 아버지격인 라틴방진을 만든 장본인이니까. 그런데 오일러의 이름만 거론되면 슬픈 두 남자가 있어. 1979년 미국퍼즐 잡지인 ‘델지’ 에 스도쿠 문제를 처음 소개한 하워드 간즈와 스도쿠라는 이름을 처음으로 붙인 일본퍼즐 잡지인 ‘노코리’ 의 카지 마키 회장이지. 이들의 이름도 기억해 두자고.


▼관련기사를 계속 보시려면?

INTRO 퍼즐 효과, 그것이 궁금해!
PART 1 수학퍼즐이 뭐기에 
PART 2 수학적 사고력에 진짜 도움이 될까?
PART 3 영재들은 왜 갖고 노는 걸까?
PART 4 수학퍼즐 200배 활용법