기하 외에도 시험장에 들어가지 못하는 과목이 있습니다. 이들은 진로 선택과목이라는 분류 아래 있는 실용수학과 경제수학입니다. 아무래도 시험에 나오지 않고 선택이라고 하니 다른 과목보다 덜 중요해 보이나요? 이제부터 그렇지 않다는 사실을 알려드리겠습니다.
실용수학은 ‘자료’, ‘규칙’, ‘공간’이라는 3가지 영역으로 이뤄져 있습니다. 자료에서는 실생활에서 쓰이는 자료를 수집해 그림, 표, 그래프로 표현한 뒤 분석하고 해석하는 방법을 배웁니다.
규칙 영역에서는 해석학과 기하학의 내용으로 피보나치 수열 같은 식에서 규칙을 찾거나 프랙털 같은 반복되는 도형의 특징과 규칙을 찾는 방법을 배웁니다. 공간에서는 건축물을 설계할 때나 그림을 그릴 때 기하학이 어떻게 쓰였고, 어떤 방법으로 응용됐는지 알 수 있지요.
규칙과 공간 영역은 기초수학인 기하의 응용을 다루고 있습니다. 이에 대해 이향숙 대한수학회장은 “기초과목인 기하와 기초수학의 응용인 실용수학이 같은 선택과목이라는 점도 문제”라고 말했습니다.
고대부터 알던 개념도 아직 유용해
이들 선택 과목도 중요한 내용을 담고 있다는 사실을 몇 가지 예로 보여드리지요.
지난 4월 10일 수학계에는 큰 경사가 났습니다. 오희 미국 예일대 수학과 석좌교수가 2018년도 제28회 호암상을 받았습니다. 호암상은 기초과학 분야에서 창의적이고 탁월한 연구 업적을 이룬 학자에게 주는 상입니다. 수학계에서 호암상 수상자가 나온 건 6년만의 일이지요.
오희 교수는 고대 그리스 수학자 ‘아폴로니우스의 원 채우기 문제’와 관련된 업적으로 상을 받았습니다. 아폴로니우스의 원 채우기 문제는 교과서에 나오는, 원을 겹치지 않고 평면을 채우는 ‘원 채우기’ 문제를 알면 이해하기 쉽습니다. 어떤 평면에서 임의의 원 3개가 겹치지 않고 접할 때 이 세 원에 접하는 원은 2개 있습니다. 이 원리를 이용해 어떤 원 안에 무한히 많은 원이 겹침 없이 접하도록 배열하는 ‘아폴로니안 개스킷’은 수학자들의 관심 분야입니다.
여기서 오희 교수는 서로 접하는 원을 무한히 반복해 채워서 프랙털을 만들 때 생기는 원의 개수와 분포의 관계를 수학적으로 규명했습니다. 프랙털은 작은 구조가 전체 구조와 비슷한 형태로 반복되는 기하학적 구조를 뜻합니다. 오희 교수의 연구는 눈송이처럼 자연에 있는 프랙털 구조의 기하학적 해석 연구에 도움이 될 전망입니다. 이처럼 고대부터 내려오던 원 채우기나 프랙털 같은 기하학 개념도 지금까지 계속해서 연구하고 있는 주제입니다.
예술가도 매료된 ‘프랙털’
프랙털은 수학자로는 부족한지 예술가들의 마음마저 홀립니다. 독특한 특성 때문에 몇 개만 반복해 그리거나 색을 덧입히면 금세 예술 작품으로 변하기 때문입니다. 이런 프랙털의 오묘한 매력에 빠져 프랙털을 이용해 예술 작품을 만드는 사람도 있습니다.

‘프랙털 아티스트’로 활동 중인 박보석 한성대학교 시각디자인학과 교수는 끊임없이 반복되는 규칙이 있는 프랙털에 매료돼 프랙털 예술을 시작했습니다. 같은 모습을 반복해서 만들어내는 나뭇가지처럼 자연의 모습을 프랙털 작품으로 만들어 내기도 하고, 프랙털과 상관없는 사물도 프랙털 개념을 이용해 표현하기도 합니다.
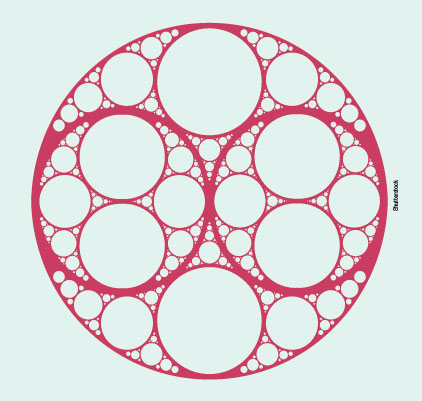
급기야는 기하학 개념 자체를 작품으로 나타내기도 합니다. 안과 밖이 없는, 경계가 하나뿐인 도형 뫼비우스의 띠나 펜로즈 삼각형을 대상으로 하면서요. 그중에서 특히 눈에 띄는 작품은 앞서 언급한 아폴로니안 개스킷을 이용한 작품입니다.
아폴로니안 개스킷을 살짝 변형한 뒤, 여기에 강렬한 붉은 색을 입히자 기하학 도형이 화려한 작품으로 재탄생했습니다. 이처럼 수학을 다양한 분야로 응용하는 방법을 실용수학 교과에서 배울 수 있습니다.
텔레비전 속 숫자 읽어주는 ‘경제지표’
물론 모든 과목이 기하학 기반인 건 아닙니다. 경제수학은 대수와 해석학을 기초로 배우는 응용 수학이지요. 이 과목은 ‘수와 생활경제ʼ, ‘수열과 금융ʼ, ‘함수와 경제ʼ, ‘미분과 경제ʼ의 4개 영역으로 이뤄져 있습니다. 특히 새로 생긴 수와 생활경제 영역에서는 비율과 비례 개념을 토대로 물가지수, 실업률, 환율, 세금 등 생활과 밀접한 경제 내용을 다룹니다. 이런 경제지표를 알고 있어야 방송이나 신문 기사를 제대로 이해할 수 있지요.
“이영자 씨는 대한민국에서 엥겔지수가 제일 높을 거예요.”
얼마 전 한 예능 프로그램에서 나온 대사입니다. 눈치껏 많이 먹는다는 건 알겠는데, 정확히 이해할 수 있나요? 독일의 사회통계학자 에른스트 엥겔은 ‘저소득층 가계일수록 총 가계지출 중 식료품 지출이 기하급수로 증가한다’는 ‘엥겔의 법칙’을 주장했습니다. 엥겔지수는 이 법칙에 이용되는 지표로, 엥겔지수가 높을수록 가계에서 식료품에 지출하는 돈이 많다는 뜻입니다.

우리가 사는 사회가 어떻게 돌아가는지를 알려면 경제수학을 배우는 게 도움이 많이 되겠지요?
자세히 알고 싶다면 ‘곡선과 그래프’
경제 현상을 분석할 때는 그래프도 필요합니다. 예를 들어 국민 소득을 나타낼 때 이용되지요. 미국의 경제학자 맥스 오토 로렌츠는 한 나라 국민의 소득 분배 상태를 분석하기 위해 로렌츠 법칙을 만들었습니다. 인구의 누적 비율과 소득의 누적 점유율 사이의 관계를 그래프로 나타냈는데, 실제 곡선과 소득이 균등할 때의 이상적인 직선이 이루는 면적의 차이로 불평등한 정도를 나타냅니다.
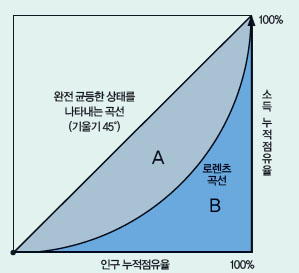
이처럼 그래프를 이용하는 경우에는 ‘부등식의 영역’을 나타내는 수학도 필요한데, 이것은 연립 부등식을 좌표에 나타내 원하는 영역의 넓이를 구하는 방법입니다. 이 단원은 원래 고등학교 1학년 때 모두 배우던 내용인데, 2015 개정 교육과정에서 경제수학의 ‘함수와 경제’ 영역에서 배우는 것으로 바뀌었습니다.
수능 시험지에는 등장하지 않아도 중요한 역할을 하는 수학이 많습니다. 시험을 잘 보는 것도 중요하겠지만, 그보다 더 먼 미래를 생각한다면 수학 소양을 폭넓게 기르는 게 좋습니다. 시험에 안 나온다고 이들을 잊지 마세요~.
▼관련기사를 계속 보시려면?