구독상품안내
눈으로 볼 수 없다면 수학적으로 우주의 모양을 생각해 볼 수 있다. 여기에 쓰이는 수학은 위상수학이다. 위상수학은 물체의 모양이 바뀌어도 변하지 않는 성질을 연구하는 수학의 한 분야다. 쉽게 말해, 구멍의 개수에 따라 물체를 분류한다. 구멍의 개수가 같으면 같은 물체로 본다. 예를 들어, 구멍이 하나인 도넛과 손잡이가 있는 컵은 같다고 본다.
위상수학자의 가장 근본적인 질문은 ‘공간을 어떻게 분류할 것인가?’다. 예를 들어 2차원 공간은 평면과 구면, 쌍곡면 총 3가지로 나뉜다. 여기서 구면이란 구의 표면이다. ‘구’라는 단어가 들어가니 당연히 3차원이라고 착각하기 쉽다. 하지만 구면 위에 있는 개미는 자신이 있는 공간을 2차원으로 생각하기 때문에 이렇게 분류한다.
우주는 3차원 구 모양?
앙리 푸앵카레는 우주의 모양에 대해 깊이 고민한 프랑스의 수학자로, 공간을 근본적으로 어떻게 이해하고 분류할지 질문을 던진 위상수학의 창시자다. 그는 1904년 논문에서 ‘푸앵카레의 추측’이라는 질문을 던졌는데, 이는 우주의 모양을 위상수학적으로 생각한 추측이었다. 쉽게 쓰면 아래와 같다.
푸앵카레의 추측
경계가 없고 유한한 3차원 우주를 한 바퀴 돌아
온 임의의 밧줄을 끌어당겨 한 점으로 모을 수
있다면, 이 우주는 3차원 구와 같다.
푸앵카레의 추측을 이해하기 위해 머릿속으로 상상해 보자. 우주 전체를 여행하고 돌아올 수 있는 우주선과, 우주 전체를 감을 수 있는 밧줄이 있다. 우주선이 밧줄을 달고 지구를 출발해 우주 전체를 돌아 지구로 돌아왔다고 해보자. 푸앵카레의 추측에 따르면, 우주가 3차원 공간이고 이 끈을 잡아당겼을 때 끈이 한 점에 모인다면 우주의 모양은 3차원 구다! 만약 구가 아니라면 끈은 어딘가에 걸려 한 점으로 모이지 않는다.
하지만 이는 어디까지나 추측이다. 게다가 거의 100년 동안 풀리지 않은 난제 중의 난제였다. 수학을 널리 알리는 활동을 하는 미국 클레이 수학연구소는 2000년에 상금 100만 달러를 걸고 7가지 중요한 수학 문제인 ‘밀레니엄 문제’를 발표했는데, 푸앵카레의 추측은 그중 하나였다.
이 추측이 풀리면 우주의 모양에 한발짝 더 다가갈 수 있었다. 한 세기 동안 많은 수학자를 좌절시킨 이 추측은 갑자기 등장한 수학자에 의해 풀린다.
3차원 기본 공간은?
푸앵카레의 추측을 해결한 사람은 러시아의수학자 그리고리 페렐만이다. 2002년에 출판 전 논문을 수집하는 인터넷 사이트, 아카이브(arXiv)에 증명을 발표했고, 국제수학연맹이 3년 동안 검증한 결과 옳은 것으로 판명이 났다. 7개의 밀레니엄 문제 중 하나가 최초로 풀리는 순간이었다.
그런데 사실 푸앵카레의 추측은 페렐만이 해결한 문제의 일부일 뿐이다. 푸앵카레의 추측이 너무 유명했던 나머지 페렐만의 업적이 제대로 알려지지 않은 것이다. 페렐만이 해결한 진짜 문제는 ‘기하화 추측’이다. 푸앵카레의 추측은 이 추측 안에 포함돼 있어 이를 해결하면 푸앵카레의 추측도 자연스럽게 풀린다. 이 문제는 미국의 수학자 윌리엄 서스턴이 1982년 출간한 논문에서 등장했다.
서스턴은 낮은 차원에서 위상수학을 연구하는 ‘저차원 위상수학’의 선구자다. 3차원 공간에 대한 서스턴의 업적 중 하나가 바로 기하화추측이다. 기하화 추측에서 던지는 질문은 ‘3차원에는 근본적인 공간이 몇 개 있을까?’다. 2차원 공간을 평면, 구면, 쌍곡면으로 나눈 것처럼, 3차원도 그와 같이 분류할 수 있는 기본 공간이 있다고 생각한 것이다.
기본 공간은 레고의 기본 블록이라고 생각하면 쉽다. 여러 개의 레고 블록을 조합해 건물을 지었다고 하자. 그러면 기본 블록과는 다른 새로운 모양이 나온다. 공간도 마찬가지로 기본 공간을 조합해 새로운 공간을 만들어 낼 수 있는데, 서스턴은 기본 공간이 정확히 몇 개가 있는지 추측했다.
3차원 기본 공간은 8개!
그는 3차원 공간을 8가지 기본 공간으로 나눌 수 있다고 생각했다. 그 이전에는 누구도 ‘3차원 공간은 몇 개로 분류할 수 있다’고 생각하지 못했다. 서검교 숙명여자대학교 수학과 교수는 “3차원 공간을 부분적으로만 이해하고 있었던 당시에 3차원 기본 공간이 8개라고 추측한 건 아주 놀라운 일”이라고 말했다.
페렐만은 이를 독창적이고 놀라운 방식으로 증명해 냈다. 위상수학과는 별개의 수학 분야인 미분기하학에서 그 아이디어를 가져왔다. 미국의 수학자 리처드 해밀턴이 고안한 ‘리치 흐름’이라는 기법을 활용한 것이다. 리치 흐름은 어떻게 휘어져 있느냐에 따라 공간을 다르게 변화시켜 나간다. 연속적으로 움직이기 때문에 위상적인 성질은 건드리지 않는다.
그런데 문제가 있다. 리치 흐름을 계속 진행하다 보면 더 이상 흐름을 진행시킬 수 없는 ‘특이점’에 도달하는 경우가 종종 생긴다. 이 개념을 최초로 생각해낸 해밀턴은 특이점 문제를 해결하지 못했다. 하지만 페렐만은 불가능한 것처럼 보였던 이 문제를 포기하지 않고 끝까지 파고들었다.
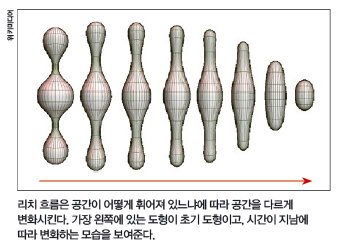
그 결과 페렐만은 특이점을 잘라냈다가 다시 봉합하는 수술을 하면 된다는 기발한 아이디어로 문제를 해결했다. 위상수학에서는 모양을 바꾸지 않고 잘랐다가 다시 붙여도 상관이 없다. 결국 페렐만은 리치 흐름으로 기하화 추측의 8가지 문제를 모두 풀었고, 그중 첫 번째가 푸앵카레의 추측이었다.
기하화 추측의 증명은 우주의 모양에 대한 실마리를 제공한다. 우주가 3차원 공간이라고 가정한다면 위에 보이는 8가지 모양 중 하나이거나, 이 8개의 조합으로 만들어져 있다고 할 수 있다. 수학자의 상상력으로 만든 우주의 모양이 과연 사실로 밝혀질 수 있을지 궁금하다.
▼관련기사를 계속 보시려면?
