d라이브러리

2002년 당시 18세였던 브리트니 갤리번은 종이를 한쪽 방향으로만 n번 접을 때 필요한 종이의 길이를 계산했다. 그리고 종이를 오른쪽에서 왼쪽으로 반 접고, 위에서 아래로 반 접고, 다시 오른쪽에서 왼쪽으로 접는 양쪽 방향 접기로 여러 번 접을 때 필요한 종이의 길이도 공식으로 만들었다. 공식에 따르면 두께가 0.1mm인 종이는 가로 약 128.7cm, 세로 약 257.4cm 길이가 있으면 양쪽 방향 접기로 10번까지 접을 수 있다. 많아야 8번밖에 접을 수 없다는 통념을 깬 것이다.
그로부터 13년 뒤, 우리나라 고등학생 다섯 명이 이 공식을 개선하고 좀 더 작은 종이로 갤리번과 똑같은 횟수만큼 접는 데 성공했다. 인천 가좌고 2학년 김나연, 노은미, 심재석, 장혜원, 조민지 학생은 가을에 열릴 학술제를 위해 작은 동아리를 결성했다. 학술제에서 발표할 연구주제로 뭐라도 떠올려야 하는 상황에서 찾은 건 ‘브리트니 갤리번의 종이접기 공식’. 장혜원 학생은 ‘접는 방법을 바꾸면 갤리번보다 더 접을 수 있지 않을까 추측했다’고 당시를 회상했다.



똑같은 종이로 더 접는 방법은?

색다른 방법으로 접어보고 싶었지만 딱 떠오르는 방법은 없었다. 학생들은 종이를 오른쪽에서 왼쪽으로 두 번, 위에서 아래로 두 번씩 번갈아 접기도 하고, 갤리번처럼 양쪽 방향으로 접다가 마지막에만 상하 또는 좌우로 연속 두 번 접어보기도 했다. 그러다가 종이를 오른쪽에서 왼쪽으로 n1번 접고, 위에서 아래로 n2번 접어 전체적으로 n1+n2번을 접는 방식에 도달했다. 학생들이 ‘순차적 종이접기’라고 부르는 이 방법을 쓰면 더 작은 종이로 갤리번과 똑같은 횟수만큼 접을 수 있다!



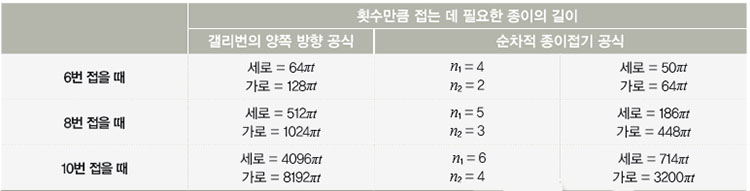
t : 종이의 두께
n1 : 가로 방향으로 접는 횟수(오른쪽에서 왼쪽으로, 또는 그 반대로 접는 횟수)
n2 : 세로 방향으로 접는 횟수(위에서 아래로, 또는 그 반대로 접는 횟수)
갤리번의 공식을 개선하다

학생들은 지도교사인 이동화 선생님과 함께 갤리번의 공식도 공부했다. 그런데 양쪽 방향 공식의
증명 과정은 인터넷에서 아무리 찾아봐도 나오지 않았다. 선생님은 ‘갤리번이 당시에 우리 학생들과 동갑이었으니 아마 수열 수준에서 증명을 했을 것’이라고 생각했고, 학생들에게 직접 갤리번의 공식을 증명해 보라고 제안했다.

양쪽 방향으로 두께가 t인 종이를 몇 번 접으면 아래 그림과 같이 가장 중심점부터 1층, 2층, 3층, 4층 …이 생기고 구조가 아주 복잡해진다. 각 층을 접는 데 필요한 종이의 가로 길이도 1πt, 2πt, 3πt, 4πt …로 모두 다르다. 참고로 이 길이는 갤리번처럼 ‘종이가 접히는 부분은 반원 모양이 된다’고 가정하고 구했다. 접힌 상태에서 종이의 두께가 반원의 반지름이 되기 때문에, (종이 두께)×π가 이 종이를 접는 데 필요한 가로 길이가 된다.

여기서 학생들은 아무리 생김새가 복잡해도 종이를 펼치면 접었던 흔적은 단순하다는 점에 집중했다. 다섯 번 접었을 때 1층과 16층에 해당하는 부분은 접힌 상태에서는 서로 포개져 있다가 종이를 펼치면 일렬로 나타난다. 즉, 16층을 접을 때 필요한 가로 길이인 16πt만큼 종이가 있으면 1층도 함께 접을 수 있다. 마찬가지로 12층을 접기 위해 필요한 가로 길이인 12πt만큼 종이가 있으면 12층과 같은 열에 있는 9층 부분도 함께 접을 수 있다.




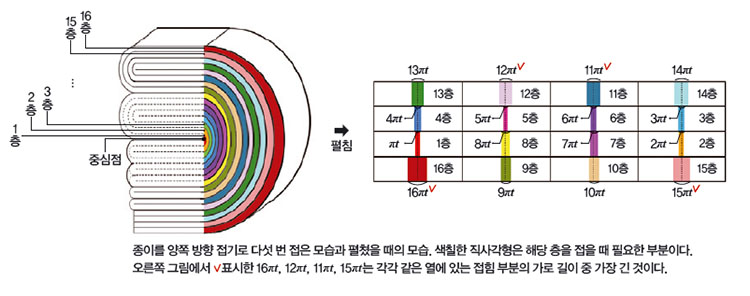
‘종이를 접는 데 필요한 가로 길이를 층별로 모두 더할 필요가 없다’는 결론을 낸 학생들은 종이를 여러 번 접은 다음 도로 펼쳐서 같은 열에 있는 사각형 중 가장 높은 층만 사인펜으로 표시했다. 예를들어 종이를 다섯 번 접고 16, 12, 11, 15층에 해당하는 부분을 표시한 다음 해당 층을 접기 위해 필요한 가로 길이인 16πt, 12πt, 11πt, 15πt를 모두 더했다. 결과는 54πt다.

그런데 갤리번의 양쪽 방향 접기 공식에 따르면 종이를 다섯 번째 접을 때 필요한 종이의 가로 길이는 n이 5일 때의 값인 64πt에서 n이 3일 때의 값인 8πt를 뺀 56πt다. 2πt만큼의 차이를 알게 된 학생들은 종이 길이의 규칙을 찾아 갤리번의 공식을 좀 더 정확하게 개선했다.

공식은 완벽하다는 생각을 접다

공식을 만들기까지 가장 어려운 점은 무엇이었을까? 갤리번의 공식과 실제로 종이를 접었을 때의 차이를 눈으로 확인하고 공식을 좀 더 정확하게 만들어 보자고 제안했던 조민지 학생은 “계산은 그렇게까지 어렵지 않았다”며 수줍게 웃었다. 종이를 열 번 남짓 접으려면 40장이 넘는 전지가 필요한데, ‘전지를 일일이 이어 붙인 다음 접고 펼치며 접힌 선과 층을 확인하는 일’이 가장 힘들었던 과정으로 꼽혔다.

학생들은 방학 동안 체육관에서 거대한 종이와 씨름하며 마침내 종이를 접는 데 필요한 가로 길이의 규칙을 찾아냈다. 이 규칙으로 만든 공식은 더 작은 종이로도 갤리번과 똑같은 횟수만큼 종이를 접을 수 있음을 알려준다. 종이를 붙이고 접는 데 4~5시간이 걸린다고 해 기자는 아쉽게도 종이가 11번 접히는 모습을 직접 보진 못했다.

학생들을 지켜본 이동화 선생님은 이 성과에 대해 “자랑스럽기도 하고, 제가 공식을 만들 일은 없을 것 같아 부럽기도 하다”며 기쁜 마음을 드러냈다. 공식이 틀렸을 리 없다는 고정관념을 깬 이들은 새해에 고3 예비수험생이 된다. 지금처럼 공식과 선택지 속에 생각을 가두지 않는 모습으로 성장하길 바란다.