d라이브러리

위상수학은 기하학에서 출발했다. 기하학을 연구하던 학자들이 20세기 들어 공간을 연구하기 시작했는데 이것이 위상수학이다. 기원전 피타고라스학파에서 다뤘던 수론이나 고대 이집트에서 시작된 기하학과 비교하면 위상수학은 굉장히 새로운 학문이다.

위상수학과 기하학은 어떻게 다를까? 전통적인 기하학은 공간을 정확히 정의하는 데 관심이 있다. 공간의 길이와 크기 등을 정확히 측정하는 게 목적이기 때문이다. 반면에, 위상수학은 공간의 전체 모양과 연결 상태를 연구한다. 위상수학은 전체 모양을 분류하는 문제로 볼 수 있다.

위상수학에서는 물체의 뚫린 구멍의 개수로 물체를 분류해 구멍의 개수만 같으면 동일한 물체로 본다. 어떤 물체를 구멍만 뚫지 않고 늘이고 줄여 똑같이 만들 수 있다면 두 물체는 같은 물체다. 그래서 도넛과 머그컵이 위상수학에서는 같다. 이렇게 위상수학은 크기를 적절히 바꿔 공간의 성질을 연구하는 학문이다.







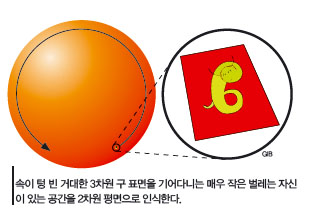
위상수학자가 보는 공간

수학자들에게 ‘다양체’는 일반 사람들이 말하는 공간의 개념과 같다. 위상수학자들의 주된 관심사는 이 다양체다. 특히, 다양체 분류는 위상수학에서 가장 근본적인 문제다.

2차원 다양체의 분류는 쉽다. 2차원 다양체는 모양과 크
기에 상관없이 구멍의 개수로만 분류하기 때문이다. 구멍개수만 같으면 적당히 구부려서 같은 물체로 만들 수 있다. 수학에서는 이 구멍의 개수를 ‘종의 개수’라고 표현한다.

2차원 다양체는 작은 범위에서 ‘전후좌우’만 있으면 정의된다. 2차원 평면이 2차원 다양체의 전형적인 예인데, 3차원 구도 겉표면만보면 2차원 다양체가 된다. 예를 들어, 커다란 구의 표면을 기어다니는 작은
벌레를 보면 벌레는 앞뒤좌우로만 움직인다. 만약 이 공간에 살고 있는 벌레가 계속 앞으로만 기어나간다면 어떻게 될까? 벌레는 분명 평면에서 앞으로만 기어가지만 언젠가 처음 출발했던 자리로 돌아오게 될 것이다.

3차원 다양체는 전후좌우에 위아래의 개념까지 들어간다. 우리가 사는 세계가 대표적인 3차원 다양체다. 그 중에서 극도로 대칭적이어서 아주 예쁜 모양을 가지는 다양체는 크게 8개로 분류할 수 있다. 윌리엄 서스턴과 그리고리 페렐만은 모든 3차원 다양체를 이 8개의 모양, 또는 그들의 조합으로 표현할 수 있다는 사실을 증명해냈다. 하지만 8개의 3차원 다양체 중 ‘쌍곡다양체’에 대한 증명은 30여 년간 미해결 문제로 남아 있었다.

한편 독일의 수학자 볼프강 하켄은 모든 3차원 다양체는 칼로 썰 듯 계속 자르면 점점 더 단순한 모양으로 바뀌어 완전히 분류할 수 있다는 ‘하켄 추측’을 내놓았다. 예를 들어, 2차원 곡선의 면을 칼로 썰듯이 적절히 잘라내면 가장 단순한 형태의 곡면으로 바뀐다. 이것이 3차원에서도 가능하다는게 하켄 추측
이다. 3차원 다양체에서의 하켄 추측은 최근까지도 위상수학자들의 가장 큰 관심사였다.