우리나라를 찾은 불청객, 메르스 바이러스
메르스 바이러스는 2012년 여름 사우디아라비아에서 처음 발견됐다. 사우디아라비아의 닥터솔리만파키병원의 바이러스 진단 연구실에서 일하던 알리 모하마드 자키 박사는 급성 폐렴과 신부전증을 앓는 60대 남성 환자에게서 피와 가래를 뽑아서 샘플을 만들었다. 거기에서 신종 코로나바이러스를 발견했는데, 이것이 ‘메르스-코로나바이러스’다.
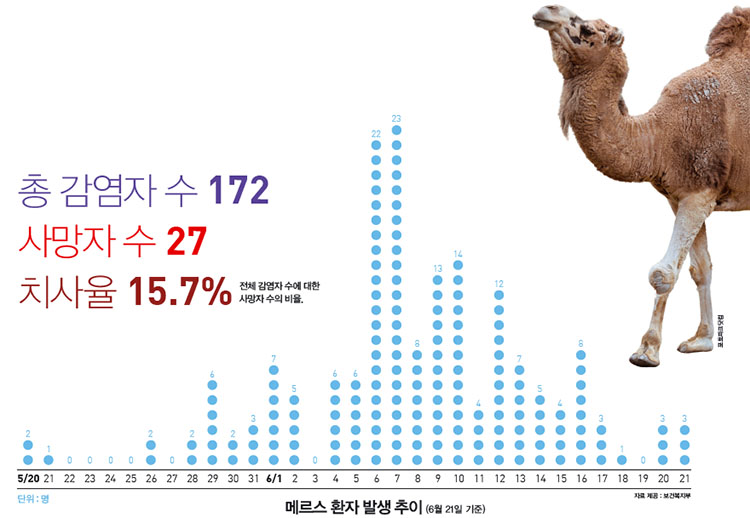
메르스 유행은 봄에 어린 낙타가 감기에 걸려서 퍼뜨린 바이러스에서 시작됐다는 설이 있다. 우리나라에서는 지난 5월 20일에 한 60대 남성이 처음 메르스 감염 판정을 받았다. 이 환자는 아라비아 반도에 있는 바레인에 다녀온 적이 있다. 어떤 경로로 감염이 된 건지는 아직 밝혀지지 않았다.
세계보건기구(WHO)에 따르면, 메르스는 환자의 침이나 가래에 섞인 바이러스가 재채기나 기침, 대화로 입, 코, 눈의 결막에 달라붙어 전염된다. 하지만 우리나라에서는 유독 먼 거리에서도 감염된 사례가 나와 감염 경로에 대한 궁금증이 커지고 있다.
메르스 바이러스는 감기 바이러스처럼 변이가 심해 백신이 없고, 메르스 감염자 가운데 사망하는 사람도 있어 모두가 긴장하고 있다.

질병 유행 분석하는 질병역학
질병역학이란 사람이 걸리는 병의 원인을 찾고, 병에 영향을 주는 요인 사이의 관계를 파악해 예방대책을 세우는 학문이다. 그중에서도 이론역학은 질병이 시작되고 유행하는 현상을 수학적으로 분석해 수식으로 정리한다. 질병역학에서 다루는 전염병 확산 모형은 전염병이 퍼지는 양상을 대략적으로 알려 준다. 그러면 전염병에 대응책을 세우는 데 도움이 된다.
실험이 불가능한 전염병은 수학 모형과 시뮬레이션의 역할이 크다. 에이즈는 전염병 확산 모형으로 감염자 수를 줄인 대표적인 예다. 미국 메릴랜드대 수학과 제임스 요크 교수팀은 에이즈 확산 모형을 통해 성관계 상대가 많은 환자 집단을 집중적으로 감시 관리했을 때 에이즈 감염자 수가 많이 줄어든다는 것을 증명했다.
전염병 확산 모형은 SIR, SEIR, SIS 등 다양하다. SIR 모형은 한 집단을 전염병에 걸릴 가능성이 있는 집단과 병에 감염된 집단, 병이 다 나은 집단으로 나눠서 시간에 따라 세 집단에 속하는 사람 수가 바뀌는 모습을 보여 준다. SIR 모형을 가장 체계적인 수식으로 처음 정리한 것은 1927년 스코틀랜드 의사 겸 전염병학자 앤더슨 맥켄드릭과 수학자 윌리엄 커맥이었다. 이들이 미분방정식을 써서 정리한 SIR 모형은 지금도 많이 쓰인다.

가장 효과적인 대책을 찾아드립니다
전염병 모형을 개발한다는 건 시간이나 환경에 따른 감염자 수의 변화를 실제와 최대한 가깝게 보여주는 식을 만드는 것이다. 전염병 확산 모형을 연구하는 경희대 응용수학과 이선미 교수는 “시간별 실제 감염자 수 데이터에 잘 맞는 모형을 만들면 효과적인 대책을 세우는 데 도움이 된다”고 설명했다.
모형을 만들려면 한 사람이 일정 시간 동안 감염시킬 수 있는 평균적인 사람 수의 비율을 뜻하는 ‘전파율(β)’ 값을 알아야 한다. 예를 들어, 평균 1/20의 확률(q)로 전염되는 병에 걸린 어떤 사람이 하루 평균 사람 10명을 만났다면 이 사람의 전파율은 10에 1/20을 곱한 1/2다. 병이 전염되는 평균 확률(q)은 질병마다 다르다. 문제는 한 사람이 접촉하는 사람 수가 그때그때 달라서 정확히 알기 어렵다는 점이다. 그래서 전파율을 추정하는 방법을 써야 한다. 추정하는 방법은 다음과 같다.
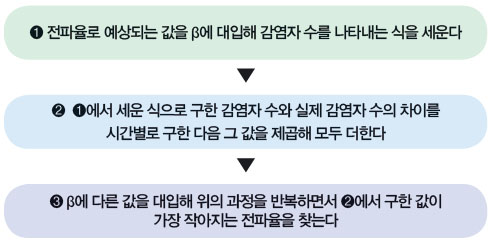
전파율을 추정해 전염병 확산 모형을 만들면 환경이 바뀌었을 때 어떤 결과가 나올지 예측하는 시뮬레이션을 할 수 있다. 이 교수는 “시뮬레이션을 통해 초기 대응을 잘 했다면 어떻게 됐을지, 실제 실행한 정책이 얼마나 효과적이었는지 등을 알아보는 것이 전염병 확산 모형 연구자 공통의 관심사”라고 밝혔다.
질병이 퍼지는 것을 막기 위해서는 예방법 홍보, 환자 격리, 병실 수 확대, 백신 투여 등 다양한 정책을 쓸 수 있다. 하지만 한정된 비용으로 가장 큰 효과를 내려면 어느 시기에 어떤 방법을 집중적으로 써야 할지 결정해야 한다. 전염병 확산 모형은 수학적인 분석으로 가장 큰 효과를 내는 데 도움이 된다.


확률 모형이 경고한 병원 내 감염
전염병 확산 모형은 질병에 따라 조금씩 달라진다. 이 교수는 “잠복기가 1년 이상인 결핵, 홍역, 말라리아 같은 질병 모형을 만들 때는 보통 미분방정식 안에 출생률과 사망률을 넣는다”고 설명했다. 사람이 태어나거나 죽으면 감염 가능성이 있는 집단(S)의 크기가 바뀌기 때문이다. 반면 인플루엔자, 사스처럼 잠복기가 며칠 안에 끝나는 질병의 모형은 집단 내 출생률과 사망률을 고려하지 않는다. 잠복기가 2주 안팎인 메르스도 마찬가지다.
인플루엔자는 잠복기가 평균 이틀 정도로 짧아 잠복기를 고려하지 않는 SIR 모형도 적합하다. 메르스는 잠복기가 그보다 길다. 그래서 잠복기에 해당하는 집단(E)이 있는 SEIR 모형이 더 적합하다.
인플루엔자처럼 감염자가 많아 연속적인 그래프를 그릴 수 있을 때는 전파율을 평균 수치로 정해 놓고 미분방정식을 세워서 만든 모형이 적합하다. 반면 메르스처럼 초기에 환자가 적을 경우에는 전파율의 값을 정하지 않고 시간에 따라 바뀌는 변수로 두는 ‘확률 모형’이 더 정확하다.
미국 조지아스테이트대 제랄도 초웰 교수팀은 SEIR 확률 모형으로 사우디 아라비아에서 메르스가 퍼진 현상을 분석했다. 연구팀은 2013년 4월부터 같은 해 10월까지 전체 감염자를 낙타에게서 전염된 환자 집단과 사람에게서 전염된 환자 집단으로 나눠 연구했다. 그 결과, 병원 안에서 사람과 사람 사이에 일어나는 전염에 특히 주의해야 한다고 강조했다. 실제로 우리나라의 메르스 감염자 대부분은 병원에서 감염됐다.

‘코르스’ 막으려면 수학 모형 필요해
누리꾼 사이에서 한국형 메르스라는 뜻의 ‘코르스’라는 말까지 나왔다. 그만큼 우리나라에서 메르스는 중동에서와 다르게 퍼졌다. 첫째, 다수를 감염시킨 ‘슈퍼전파자’가 여러 명 생겼다. 둘째, 메르스 환자와 다른 병실을 썼거나 마주친 적이 없는 경우에도 감염된 사례가 많았다. 그래서 메르스가 공기를 통해 전염될 가능성이 논란이 됐다.
질병관리본부와 함께 2009년에 우리나라에서 유행한 신종 인플루엔자 확산 모형을 개발했던 건국대 수학과 정은옥 교수는 “데이터에 근거한 수학 모형은 감염 확산 예측과 대응, 그리고 정책에 과학적 근거를 제시하는 중요한 도구다. 전염병 대유행이 끝난 뒤에도 장기적인 관점에서 연구를 해야 하지만 수학 모형의 중요성을 잘 모르는 사람이 많다”고 토로했다.

메르스를 교훈으로!
전염병 모형을 꾸준히 연구하면 다른 병에 대처할 때도 도움이 된다. 정 교수는 수도권 시민의 통근·통학 데이터를 토대로 2009년 신종 인플루엔자 확산 모형을 만들었다. 이런 경험이 모여 다음 전염병 모형을 더욱 빠르고 정확하게 만들 수 있다. 연구를 할 때는 여러 분야의 전문가가 협력해야 한다. 전염병이 퍼지는 현상은 특정 공식으로 설명할 수 없고, 감염자 수와 같은 실제 데이터를 토대로 설명해야 하기 때문이다.
이번 메르스 확산도 마찬가지다. 고려대 예방의학교실 천병철 교수는 수학동아와의 전화 인터뷰에서 “질병관리본부에 보건통계를 전문적으로 다루는 부서가 없는 것도 문제지만, 정부와 민간 통계전문가가 협력하는 합동조사를 기대하기 어렵다는 게 더 큰 문제”라고 밝혔다. 신종 인플루엔자부터 메르스까지 대규모 전염병 위협이 계속되는 만큼 수학자를 포함한 여러 전문가가 모여 적극적이고 지속적으로 전염병에 대응해야 한다.