‘최고의 한 수는 과연 어딜까…?’
문득 신이 내린 계산력을 가졌다는 우리 동네의 바둑 고수가 생각났다. 혹시 그에겐 ‘수학으로 두는 특별한 한 수’가 있지 않을까?

그렇다면 착수할 수 있는 경우의 수는 얼마나 될까? 교차점의 갯수만 하더라도 무려 19×19=361가지이므로, 그 수가 무척 많다는 걸 예상할 수 있다.
19×19 바둑판의 착수 경우의 수를 구하기 위해, 먼저 가로와 세로가 각각 2줄로 이뤄진 가장 간단한 격자 바둑판을 생각해 보자. 이때 교차점은 4개다. 그리고 각 교차점에서 일어날 수 있는 경우는 흑돌을 두는 경우, 백돌을 두는 경우 또는 아무 것도 두지 않는 경우로 총 3가지다.
각각의 점마다 3가지 경우의 수가 있으므로, 바둑돌을 둘 수 있는 전체 경우의 수는 3⁴=81가지다. 81가지의 경우의 수를 전부 나타내면 아래 그림과 같다.

그러나 81가지 경우가 모두 착수 가능한 것은 아니다. 바둑에서는 상대방의 집에는 돌을 둘 수 없다는 규칙, 즉 착수 불가능한 곳이 있기 때문이다. 예를 들어 그림❶과 같은 경우는 이미 흑돌 세 개로 흑집을 만들었기 때문에 나머지 칸에 백돌을 둘 수 없다.

마찬가지로 그림❷ 역시 백돌 2개로 백이 두 집을 만들었기 때문에, 흑돌을 둘 수 없는 착수 불가능한 경우가 된다. 이와 같이 착수 불가능한 경우 24가지를 제외하면 총 57가지 경우의 수가 나온다. 이는 전체 81개의 경우의 수에서 약 70%에 해당하는 값이다.
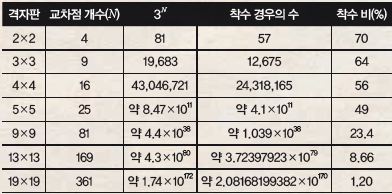
그렇다면 19×19인 바둑판에서의 착수 경우의 수는 얼마나 될까? 네덜란드 컴퓨터 과학자 존 트롬프는 바둑판의 격자가 2×2인 경우부터 착수 경우의 수와 그 착수 비를 계산했다. 결과는 아래 표와 같았다.
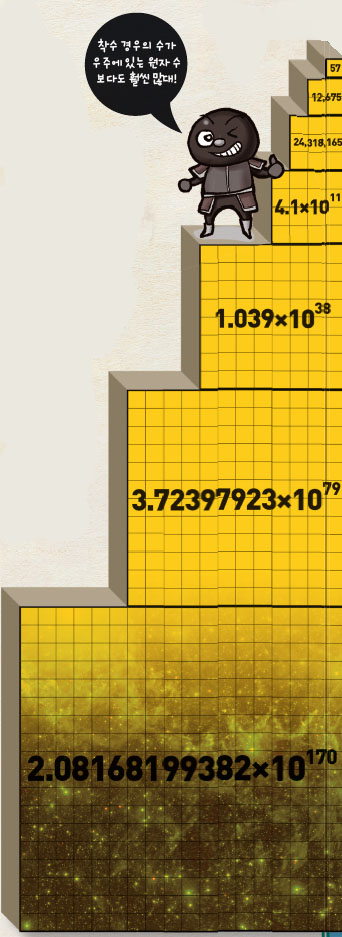
격자의 크기가 커질수록 착수 경우의 수는 급격히 커지고, 착수 비는 점점 줄어들어드는 것을 알 수 있다. 19×19인 격자인 경우 착수 비는 약 1.2%로 작지만, 경우의 수는 무려 2.08×${10}^{170}$나 된다. 이 값은 10의 100제곱을 뜻하는 ‘1구골’보다도 훨씬 더 큰 값으로, 우주에 있는 원자의 개수인 12×${10}^{78}$보다도 비교할 수 없을 만큼 큰 수다.

수학적으로 완벽한 포석을 하려면 어떻게 해야 할까? 먼저 돌을 두는 곳에 따라 얼마만큼의 힘이 전체에 미치는지를 수식으로 표현하는 것이 필요하다. 이 때문에 컴퓨터 바둑을 연구하는 학자들은 바둑의 형세를 판단하기 위해 필요한 함수를 만들었다. 이것을 ‘세력 함수’라고 한다.
일반적으로 바둑돌의 힘은 돌 중심에서부터 바깥으로 뻗어 나가며, 거리에 따라 힘이 감소한다. 이런 원리를 기초로 컴퓨터 바둑을 연구하는 중국의 켄 첸 교수는 간단한 형태인 ‘지수함수’를 이용해 세력함수를 다음과 같이 정의했다. 지수함수는 비선형 함수 중 증가, 감소를 나타내기 쉬운 대표적인 함수다. 단, d는 바둑돌과 세력을 받는 지점 사이의 최단 거리를 뜻한다.
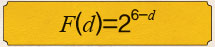
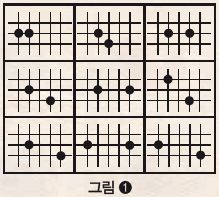
그런데 이 함수에서 지수는 왜 6-d일까? 이것은 바둑 이론에서의 ‘두터움’이라는 개념과 관련이 있다. 두 바둑돌이 서로 힘을 형성하려면 일반적으로 오른쪽 그림❶과 같이 아홉 가지 형태 중 하나여야 하는데, 적어도 두 돌이 서로 힘을 받으려면 6칸 이내에 있어야 한다. 쉽게 말해 돌들이 손을 뻗고 있다면, 적어도 6칸 이내에 있어야 서로 손을 잡을 수 있다는 뜻이다. 이런 이유로 첸 교수는 d의 최댓값이 6이라는 것을 고려해 지수의 식을 정했다.

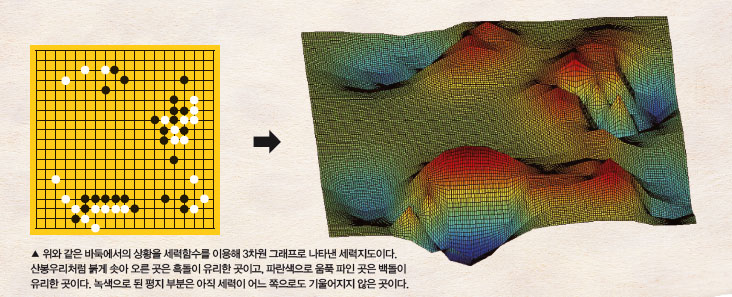
한편 우리나라 컴퓨터 바둑학자인 이병두 교수는 또 다른 세력함수를 제안했다. 이 교수는 두 바둑돌이 6칸보다 멀리 떨어져 있는 경우, 급격히 세력이 감소한다는 경험적 성질을 반영하기 위해 밑이 e인 지수함수로 정의했다. 함수식은 다음과 같다. 이때 흑돌의 세력 값을 구할 땐 상수 c를 +64로, 백돌의 세력 값을 구할 땐 상수 c를 -64로 둔다.

 실제로 오른쪽 그림❷두 세력함수를 이용해 흑돌의 세력을 구하면, 각각 F(2$\sqrt{2}$)=${2}^{6-2\sqrt{2}}$≒9.00과 I(2$\sqrt{2}$)=64×${e}^{-2}$≒8.66로 거의 비슷한 세력 값이 나온다. (단, 이때의 거리 d는 유클리드 거리로 계산한다.)
실제로 오른쪽 그림❷두 세력함수를 이용해 흑돌의 세력을 구하면, 각각 F(2$\sqrt{2}$)=${2}^{6-2\sqrt{2}}$≒9.00과 I(2$\sqrt{2}$)=64×${e}^{-2}$≒8.66로 거의 비슷한 세력 값이 나온다. (단, 이때의 거리 d는 유클리드 거리로 계산한다.)
바둑의 여러 분야 중에서도 유일하게 수학자에 의해 완벽하게 해결된 부분이 있다. 바로 ‘끝내기’다. 끝내기란, 바둑의 후반부로서 대국을 마무리하는 과정을 뜻한다.
끝내기를 연구한 수학자는 미국의 수학자 얼윈 벌리캄프다. 벌리캄프는 미국 버클리대 수학과 교수이자 조합 게임 이론 분야에서 유명한 석학으로, 1994년에 바둑의 끝내기를 수학적으로 분석한 내용을 담은 <;수학적 바둑(Mathematical Go)>;이란 제목의 책을 냈다. 수학적인 방법을 통해 끝내기 상황에서 완벽한 수를 찾은 것이다.
그럼 벌리캄프의 저서에 나오는 유명한 끝내기 문제를 통해 수학적으로 완벽한 한 수를 어떻게 찾는지 직접 구해 보자.
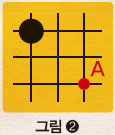
바둑에서 어떤 점 P의 가치는 (점 P에 흑돌을 놓았을 때의 가치)+(점 P에 백돌을 놓았을 때의 가치)로 구한다. 수학에서의 기댓값을 구하는 방법과 비슷하다.
예를 들어 왼쪽과 같은 상황에서 점 A의 가치를 구해 보자. 점 A에 흑돌을 놓으면 흑집 1개가 생긴다. 또 점 A에 백돌을 놓으면 백집은 생기지 않는다. 따라서 점 A의 가치를 구하는 식은 다음과 같다.


이와 같은 방법으로 점 B, C, D, E의 가치를 구하면 다음과 같다.

착수 가능한 점 A, B, C, D, E 각 점의 가치를 비교하면 $\frac{1}{2}<;\frac{5}{4}<;\frac{17}{8}<;\frac{49}{16}<;\frac{129}{32}$로, 이 상황에서는 점 E의 가치가 가장 크다는 것을 알 수 있다. 따라서 흑은 점 E에 먼저 착수해야 한다는 결론이 나온다. 수학으로 최선의 수를 찾은 것이다.
하지만 벌리캄프의 연구 결과를 실제 바둑에 적용하는 것은 무리다. 벌리캄프의 끝내기 이론을 적용하기 위해서는 흑돌과 백돌이 모두 살아 있고, 두 돌의 그룹은 서로 독립적이어야 하기 때문이다.(실제 바둑 상황에서 이런 경우는 드물다.)
그럼에도 불구하고 벌리캄프의 연구는 특별한 의미를 갖는다. 바둑의 여러 분야 중에서 논쟁없이 완벽하게 증명된 분야이며, 이 연구 결과가 또 다른 수학적 바둑 연구의 초석이 될 수 있기 때문이다.
하지만 벌리캄프의 연구 결과를 실제 바둑에 적용하는 것은 무리다. 벌리캄프의 끝내기 이론을 적용하기 위해서는 흑돌과 백돌이 모두 살아 있고, 두 돌의 그룹은 서로 독립적이어야 하기 때문이다.(실제 바둑 상황에서 이런 경우는 드물다.)
그럼에도 불구하고 벌리캄프의 연구는 특별한 의미를 갖는다. 바둑의 여러 분야 중에서 논쟁없이 완벽하게 증명된 분야이며, 이 연구 결과가 또 다른 수학적 바둑 연구의 초석이 될 수 있기 때문이다.




현재 컴퓨터 바둑의 실력은 약 1급 정도다. 프로기사들의 선수 실력과 비교했을 때, 한참 부족한 실력이다. 컴퓨터 기술이 엄청난 속도로 발전하고 있음에도 불구하고, 컴퓨터 바둑의 실력이 1단도 되지 못하는 이유는 뭘까? 그 이유는 바둑이 매우 복잡한 게임이기 때문이다.
게임의 복잡한 정도를 나타내는 개념으로는 ‘상태공간 복잡도’와 ‘게임나무 복잡도’가 있다. 상태공간 복잡도란, 게임 초기상태로부터 착수 가능한 모든 수로 정의한다. 바둑의 경우 361개의 교차점이 있고, 각 점에 대해 흑돌, 백돌, 빈 공간과 같이 3가지의 경우가 있으므로 상태공간 복잡도의 값은 ${3}^{361}$가 된다.
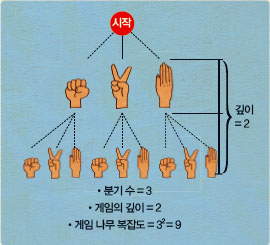
두 번째 게임나무 복잡도는 게임에서 일어나는 모든 상황을 ‘나무’와 같이 줄기와 가지로 표현하는 것이다. 수학에서는 이와 같이 나뭇가지와 모양을 닮은 그림을 ‘수형도’라고 한다. 게임나무 복잡도는 게임나무의 분기 수와, 게임나무의 깊이만 알면 ${(분기 수)}^{깊이}$로 쉽게 구할 수 있다.
예를 들어 A와 B 두 사람이 즐기는 간단한 게임인 ‘가위 바위 보’의 게임나무 복잡도를 구해 보자. 각 사람이 낼 수 있는 경우의 수 3은 분기 수, 나무의 시작부터 끝까지 걸리는 단계 수인 2가 게임의 깊이다. 따라서 가위 바위 보의 게임나무 복잡도는 3²=9다.
그렇다면 바둑의 게임나무 복잡도는 어떻게 구할까? 바둑에서는 두 사람이 돌을 두는 상황에 따라 착수 경우의 수가 달라진다. 즉, 처음부터 끝으로 갈수록 그 수가 줄어든다. 또 두 사람이 몇 번을 둬야 게임이 끝나는가를 구하는 게임의 깊이도 일정하지 않다.
이러한 이유 때문에 컴퓨터 과학자들은 여러 횟수의 게임을 통해 바둑의 분기 수와 게임의 깊이를 통계적으로 추정하고 있다.
호주의 심리학자 버마이스터는 바둑의 분기 수는 200, 게임의 깊이는 250~300 정도로 계산했다. 버마이스터가 계산한 값으로 바둑의 게임나무 복잡도를 구해 보면, 그 최댓값은 약 ${10}^{575}$로 천문학적인 수가 나온다. 이 값은 게임나무 복잡도가 ${10}^{123}$인 체스보다도 무려 ${10}^{452}$배가 큰 값이다. 이 때문에 완벽한 수를 두는 컴퓨터 바둑을 개발하는 것은 무척 어려운 일이다.





Enjoy 1 바둑판을 바꿔 보라!
바둑판의 모양이 바뀌면 바둑은 어떻게 달라질까? 이런 궁금증을 가지고 직접 바둑판의 모양을 바꿔 본 과학자가 있다. 우리나라 고등과학원 계산과학부의 김재완 교수다.
김재완 교수는 양자역학 분야의 전문가로, 박사학위 시절 축구공과 모양이 비슷한 탄소 분자인 ${C}_{60}$의 성질을 연구하고 있었다. 그러던 중, 문득 ‘축구공과 비슷한 이 탄소 분자 모양에 바둑을 두면 어떨까?’란 생각을 하게 됐다. 이런 생각에서 아이디어를 얻어 만들게 된 것이 바로 육각형 모양의 바둑판이다. 그 모양이 거북의 등과 닮아 ‘거북 바둑’이라는 이름도 있고, 탄소의 나노구조에서 아이디어를 얻어 ‘나노 바둑’이라고 부르기도 한다.
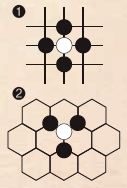
이렇게 바둑판의 모양을 바꾸면 게임은 어떻게 달라질까? 바둑판의 모양이 사각형인 경우에는 바둑판의 가장자리를 제외하면 그림❶과 같이 한 집을 만들기 위해 4개의 돌이 필요하다. 그러나 육각형 모양의 바둑판에서는 그림❷와 같이 돌 3개만으로도 한 집을 만들 수 있다. 이러한 성질 때문에 육각 바둑은 사각 바둑보다 게임이 훨씬 빠르게 진행되고, 판세가 쉽게 뒤집어질 수 있다. ‘역동적인 바둑’이 되는 것이다.
Enjoy 2 바둑돌로 수학퍼즐을! 님(Nim) 게임
바둑돌을 이용해 즐길 수 있는 재밌는 수학적 전략게임이 있다. ‘님(Nim) 게임’이다. ‘Nim’은 독일어 ‘Nimm’에서 따온 말로 영어의 Take(가져가다)의 뜻과 같은 뜻이다. 님 게임은 바둑돌 여러 개를 두고 두 사람이 번갈아가며 하나나 둘, 또는 세 개의 바둑돌을 가져갈 때 맨 마지막에 남은 바둑돌을 가져가는 사람이 지는 게임이다.
만약 탁자 위에 바둑돌이 13개 있고, 두 사람 A와 B가 게임을 한다고 하자. 님 게임에서 A가 반드시 이길 수 있는 필승 전략은 뭘까?
문제를 풀기 위해 과정을 거꾸로 생각해 보자. 먼저 13개의 바둑돌을 다음과 같이 4개씩 나눠 보자. 이때 맨 마지막에 남은 한 개의 돌을 B가 가져가야 A가 이긴다.

바둑돌을 최소 1개부터 최대 3개까지 가져갈 수 있으므로, B가 처음에 2개를 가져갔다면 A는 B가 가져간 바둑돌과 더했을 때 4가 되는 바둑돌, 즉 2개를 가져가야 한다. 두 번째에서 또 B가 만약 3개를 가져갔다면, A는 1개를 가져가야 한다. 이런 방법으로 B는 (A가 가져간 돌의 개수)+(자신이 가져간 돌의 개수)=4가 되면 반드시 이 게임에서 이기게 된다. (단, 반드시 이 게임에서 B가 먼저 돌을 가져가야 한다.)

Enjoy 3 바둑돌로 계산도 한다!
0과 1, 두 숫자로 수를 나타내는 것을 ‘이진법’이라고 한다. 바둑돌은 흑돌과 백돌, 두 가지 색의 돌로 이뤄져 있어 바둑돌을 이용해 이진법을 이해하기에 쉽다.
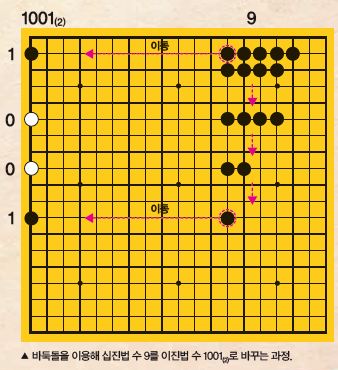
바둑돌을 이용해 십진법 수를 어떻게 이진법으로 바꿀 수 있을까? 흑돌을 1, 백돌을 0이라고 가정한 다음, 다음 규칙을 따라해 보자.
규칙 1 바둑돌이 홀수 개인 경우
반으로 나누기 위해 바둑돌 한 개를 왼쪽에 준 다음, 남은 바둑돌을 반으로 개수를 줄여 한 줄 내려온다.
규칙 2 바둑돌이 짝수 개인 경우
바둑돌이 반으로 나눠지므로 왼쪽에 흰돌을 놓고, 반으로 개수를 줄여 한 줄 내려온다.
규칙 3 바둑돌이 1개만 남을 때까지 규칙1과 2를 진행한다. 그러면 왼쪽에 있는 백돌과 흑돌로 이진법 수를 확인할 수 있다.

Enjoy 3 바둑돌로 계산도 한다!
0과 1, 두 숫자로 수를 나타내는 것을 ‘이진법’이라고 한다. 바둑돌은 흑돌과 백돌, 두 가지 색의 돌로 이뤄져 있어 바둑돌을 이용해 이진법을 이해하기에 쉽다.
바둑돌을 이용해 십진법 수를 어떻게 이진법으로 바꿀 수 있을까? 흑돌을 1, 백돌을 0이라고 가정한 다음, 다음 규칙을 따라해 보자.
규칙 1 바둑돌이 홀수 개인 경우
반으로 나누기 위해 바둑돌 한 개를 왼쪽에 준 다음, 남은 바둑돌을 반으로 개수를 줄여 한 줄 내려온다.
규칙 2 바둑돌이 짝수 개인 경우
바둑돌이 반으로 나눠지므로 왼쪽에 흰돌을 놓고, 반으로 개수를 줄여 한 줄 내려온다.
규칙 3 바둑돌이 1개만 남을 때까지 규칙1과 2를 진행한다. 그러면 왼쪽에 있는 백돌과 흑돌로 이진법 수를 확인할 수 있다.