d라이브러리

두 번 모두 져 독기가 오른 신라의 김유신. 이대로 무너질 수 없다며 윷놀이에 모든 걸 걸고 한판 승부를 펼치자고 나선다. 반면 적지 않은 영토를 확보해 느긋한 고구려의 연개소문과 백제의 계백. 김유신의 ‘다걸기(올인)’ 전략을 역으로 이용하려 하는데….

김유신·연개소문·계백·소정방 네 장수의 윷놀이 한판

“이판사판이다. 우리 땅 전부를 걸 테니 너희도 다 걸어라!” 김유신의 이런 오기를 짐작한 계백과 연개소문은 윷놀이 전에 서로 밀약을 맺었다. 백제나 고구려 둘 중 하나가 이기면 서로의 영토는 놔두고 이긴 나라가 신라의 땅을 갖기로. “그래 한 번 해보자. 대신 무르기 없기다.” 계백과 연개소문은 김유신의 다걸기 전략을 역이용하기로 맘먹고 승부를 받아들인다.
 

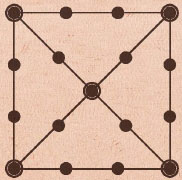
김유신, 연개소문, 소정방, 계백 순으로 윷을 던진다. 초반에 김유신의 말이 빠르게 움직인다. 하지만 경기가 계속되면서 판세가 달라진다. 종반에 접어든 상황, 김유신의 말이 가장 느리다. 계속 말이 잡혀 말 1개가 날개에, 1개는 뒷모개에, 2개는 도에 한 묶음으로 놓여 있다. 반면 연개소문은 가장 빠르다. 말 3개가 났고 말 1개는 찌윷에 놓여 있다. 말 2개가 난 계백은 뒷모도에 말 1개, 날걸에 1개가 있다. 소정방의 말은 속모와 뒷밭, 날도에 1개씩 있고, 나머지 1개는 출발도 하지 않은 상태다(그림 1).

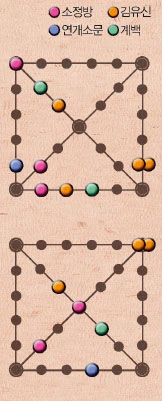
소정방 차례다. 걸이 나왔는데 날개에 있는 김유신의 말을 모른 척하고 걸 자리에 새 말을 놓는다. 서로 먼저 나려는 계백과 연개소문은 여기에 신경 쓰지 않는다. 계백은 걸이 나와 잠깐 고민하더니 날걸의 말을 나는 데 활용한다. 김유신은 개가 나와 도에 있는 말 2개로 걸에 있는 소정방의 말을 잡는다. 다시 윷을 얻고, 또 한 번더 던져 개가 나온다. 걸에 있던 말 2개를 2칸 움직여 앞밭(모)으로 옮기고, 날개에 있는 말을 조금 전에 얻은 윷으로 난다.

 “내 이름이 왜 개소문인지 아나? 윷에서 개가 너무 잘 나와 이게 소문이 나서 그래, 하하. 자 개 나와라!” 연개소문이 던진 윷은 신기하게도 개다. 기분 좋게 날도에 있는 소정방의 말을 잡고 한 번 더 윷을 던진다. 또 개가 나와 날걸로 말을 옮긴다. 다음에 걸 이상만 나오면 날 수 있다.

소정방은 걸이 나온다. “내가 방을 무지무지 좋아해 이름에 방자가 들어간다 해” 하며 뒷밭의 말을 방으로 옮긴다. 이번에도 김유신을 밀어주기 위한 움직임이다. 방에 말을 옮김에 따라 계백이 걸이 나오면 김유신은 도, 개, 걸 어느 것이 나와도 상대 말을 잡을 수 있다. 물론 개가 나와 방의 말을 잡고 계백이 더 전진할 수도 있다. 하지만 이때도 도나 개가 나오면 김유신에게 잡힐 가능성이 생긴다. 계백은 걸이 나와 사려로 말을 이동한다(그림 2).

 “김윷신이란 말 들어봤나? 우리나라에선 내가 윷신으로 통한다 이거야. 모 나와라~!” 판세는 불리해도 여전히 자신감이 넘치는 김유신은 다시금 말을 앞세우며 평소와 달리 윷을 굴린다. 그의 바람대로 모가 나온다. 다시 던진 윷은 걸, 앞밭의 말 2개로 방 자리에 있는 소정방의 말을 잡고 또 기회를 얻는다. 판세가 완전히 뒤집혔다. 이제 걸만 안 나오면 된다. “걸 나와라”라며 계백과 연개소문이 소리친다. 하지만 김유신이 던진 윷은 도를 가리킨다. “이겼다!” 사려 자리의 계백 말을 잡을 수도 있지만 김유신은 뒷모개의 말을 방으로 옮겨 말 3개를 묶어 처음 나온 모로 난다.

윷놀이

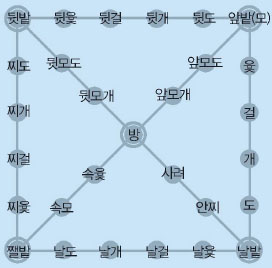
규칙 ① 각자 말과 윷 4개를 준비한다. 말은 주위에서 쉽게 구할 수 있는 바둑알이나 장기알, 돌, 동전 등을 이용하는데, 보통 말을 4개씩 쓴다.

규칙 ② 윷과 모가 나오거나 상대의 말을 잡았을 때는 윷을 던질 기회를 한 번 더 얻는다.

규칙 ③ 같은 편의 말이 한 자리에 모이면 그때부터는 한 묶음으로 이동한다. 잡힌 말은 모두 처음부터 시작한다. 윷자리 명칭은 지역마다 조금씩 다르다.

윷보다 모가 적게 나오는 이유
 

“말도 안 돼! 인정할 수 없어. 소정방이 김유신을 도와줬기 때문에 정당한 시합이 아니야!” 계백과 연개소문은 자신들이 유리할 때는 아무 말도 하지 않다가 막상 김유신이 막판 대역전극을 펼치자 항변하기 시작한다. 그러나 이미 승부는 끝났다.

사실 전통놀이의 모든 승부는 치밀한 김유신의 계략에 따라 진행됐다. 고누와 쌍륙에서 져도 윷놀이에서 다걸기 전략을 쓰면 상대가 받아들일 것이라 생각하고, 오래전부터 소정방과 많은 윷놀이를 하며 상대 모르게 소정방이 김유신을 돕는 전략도 세웠다. 이렇게 세 장수의 전통놀이 삼국대전은 신라가 막판 대역전극을 펼쳐 삼국을 통일하며 끝난다. 하지만 당나라의 소정방이 김유신과 맺은 밀약보다 더 많은 영토를 요구하면서 당나라와 신라는 나중에 전쟁에 돌입한다.

전문가들은 윷놀이가 재미있는 수학적인 이유를 단순하면서도 승부를 예측하기 어려운 변수가 많다는 점을 꼽는다.  4가지 길로 이동해 말 이동에 관한 변수와 윷이라는 예측할 수 없는 변수에 따라 웃고 우는 대반전이 가끔 일어나기 때문이다.

윷은 평면과 곡면 어느 쪽이 바닥에 놓이느냐에 따라 그 결과가 달라진다. 4개의 윷이 만들 수 있는 경우는 총 16가지인데, 이 중 첫 번째 윷만 뒤집히는 경우와 두 번째 윷만 뒤집히는 경우처럼 서로 같은 상황을 모두 합하면 우리가 이용하는 도, 개, 걸, 윷, 모 5가지로 압축된다.
 

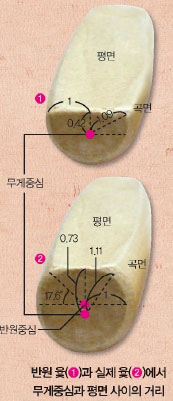
이런 특성을 고려해 윷의 곡면이 뒤집어지는 확률을 구할 수 있다. 반지름이 1인 반원 윷은 무게중심이 평면 중심에서 아래로 0.42만큼 떨어져 있고, 무게중심에서 평면모서리까지의 거리는 1.09다. 널리 사용되는 실제 윷은 반원 중심에서 각도가 17.6°만큼 곡면이 더 있는데, 이에 따라 무게중심은 평면 중심에서 아래로 0.73, 무게중심에서 평면 모서리까지의 거리는 1.11이다.

그런데 윷은 굴리거나 던질 수 있다. 허명회 고려대 통계학과 교수팀의 연구에 따르면 곡면이 위를 향하는(윷이 엎어지는)비율의 경우 윷을 굴릴 때는 반원 윷은 57%, 실제 윷은 59%인 반면, 던졌을 때는 반원 윷은 37%, 실제 윷은 33%로 크게 차이가 났다. 이런 차이는 윷을 굴릴 때는 운동에너지에 따라 무게중심의 위치가 변하면서 곡면이 나타날 확률이 결정되지만 던질 때는 회전중심에 따라 달라지기 때문이다. 윷을 던질 때보다 굴릴 때 곡면이 위를 향할 가능성이 높은 이유는 굴러갈 때 평면이 바닥과 맞닿으면 더 구르기 어렵지만 곡면이 바닥에 닿으면 더 잘 굴러간다는 점을 생각하면 이해하기가 쉽다.

이에 따라 도, 개, 걸, 윷, 모의 확률을 이론적으로 계산하면 실제 윷을 굴릴 때는 34%, 35%, 16%, 3%, 12%가 나오며, 던질 때는 10%, 29%, 40%, 20%, 1%가 나온다. 굴릴 때는 모의 확률이 윷보다 높은 반면, 던질 때는 윷의 확률이 도보다 높다. 우리가 아는 일반적인 값과는 차이가 크다.

그런데 실제 윷놀이에서도 이렇게 나타날까? 허 교수팀은 실제 윷을 1132번 굴리고, 1120번 던져 이론적인 값과 비교를 했다. 그 결과 굴렸을 때는 이론값과 비슷했으나 던졌을 때는 도는 20%, 개는 31%, 걸은 34%, 윷은 12%, 모는 3%로 나타나 이론값과 다른 경험값을 얻었다. 이런 차이는 윷을 던질 때 일부는 바닥에 떨어져 구르기도 하고, 바닥이나 바람 등 다른 요인에 따라서도 영향을 받기 때문으로 보인다.
 

✚윷놀이와 비슷한 인도의 파치시
 

윷놀이는 현재도 설날과 정월 대보름, 추석 등 명절에 가장 인기 있는 전통놀이다. 도, 개, 걸, 윷, 모는 부여의 관직명인 저가(도), 구가(개), 우가(윷), 마가(모)에서 왔으며, 걸은 노새를 가리키는 거루에서 왔다고 한다. 지금은 도는 돼지, 개는 개, 걸은 양, 윷은 소, 모는 말로 본다. 이들은 모두 사람과 함께 사는 가축으로 크기와 달리는 속도에 따라 붙여진 것으로 보인다.

많은 학자들은 페르시아의 파치시가 중앙아시아를 거쳐 인도의 파치시(사진)로, 중국으로 들어가‘저포’로, 이것이 우리나라로 와 ‘윷’이 됐다고 본다. 하지만 일부 학자는 윷이 우리나라 남부 지방에서 나왔다고도 한다. 각종 자료를 살펴보면 비록 형태와 모양은 조금씩 차이가 나지만 남아메리카와 북아메리카 대륙의 원주민들도 윷을 즐겨 놀았던 것으로 확인된다.

대표적인 전통놀이인 윷놀이는 우리나라에서만 인기가 있는 게 아니다. 외국에서도 수학교육에 활용될 정도로 관심이 높다. 외국의 많은 초중등 교육기관에서 다양한 문화와 결합된 수학을 체험하는 기회로 여러 나라의 전통놀이를 수업에 활용한다. 우리나라 놀이로는 윷놀이와 고누가 소개된다. 이처럼 윷놀이는 세계에서도 인정받는 수학 놀이다.

윷의 확률

허명회 교수팀의 연구에 따르면 윷을 굴릴 때는 평면이 위로 향할 때와 곡면이 위로 향할 때(엎어진 모양)의 무게중심과 이들이 나타나기위한 모양이 가질 수 있는 최대 무게중심의 높이 차이(a와 b)로 윷의 확률이 결정된다. 반면 던질 때는 바닥에 닿을 때 회전중심의 각(A)이 중요하게 작용한다.

윷 대신 주사위를 이용하면 어떨까?
 

윷가락이 없다는 이유로 윷놀이를 하지 못하는 경우가 있다. 다른 도구를 이용할 순 없을까? 숟가락은 가장 쉽게 윷을 대신할 수 있는 도구다. 아래가 둥글고, 무게중심이 아래쪽에 있어 엎어질 확률이 낮다. 물론 숟가락의 모양이나 재질 등에 따라 윷과 차이가 클 수 있다.

반면 놀이에 가장 널리 사용되는 주사위는 윷놀이에도 잘 어울린다. 대신 윷이 보이는 변화와는 다른 값을 기대해야 한다. 윷에서 3칸을 가는 걸이 나오는 확률과 주사위에서 눈금 3이 나오는 확률이 다르기 때문이다. 특히 주사위는 최대 6칸을 이동할 수 있어 윷을 이용할 때와 매우 다른 모습이 펼쳐질 수 있다.

우리가 이용하는 윷판은 최대 5칸을 이동할 수 있는 모에 알맞게 맞춰져 있다. 따라서 이용하는 도구가 달라진다면 말판도 바뀌어야 서로 어울린다. 즉 주사위를 이용한다면 말판의 경로가 6번째 칸에서 교차점이 나타나도록 수정할 필요가 있다. 이렇게 하면 모든 교차점까지 1개 또는 2개의 지점이 더 생기게 된다. 새로운 윷놀이가 만들어지는 셈이다.

그런데 2개의 윷으로도 윷놀이를 할 수 있을까? 역시 같은 방법으로 지점의 개수를 2개씩 줄이면 가능하다. 물론 이처럼 윷과 말판을 바꾼 새로운 윷놀이가 얼마만큼 재미있을지는 미지수다. 기존의 윷놀이는 오랜 시간이 흐르면서 적당한 시간동안 가장 재미있게 놀 수 있도록 4개의 윷에 최적화된 상태다.

정달영 숭실대 수학과 교수와 이광연 한서대 수학과 교수 등 수학자들은 “4개의 윷과 현재의 윷판은 수학적으로도 가장 재미있는 형태”라고 입을 모은다. *그래프이론에 따르면 윷놀이는 가장 단순화된 최적 경로 찾기로 볼 수 있다. 수학이 어떤 해법을 구할 때 가능하면 가장 쉽고 단순한 방법을 찾으려고 한다는 점에서 볼 때 윷놀이는 이런 특성을 가장 잘 충족시켜주는 놀이인 셈이다. 즉 수학적으로 윷판을 더 복잡하고 다양하게 변형시킬 수는 있겠지만 현재의 구조가 재미있게 놀기에 가장 적합한 형태라는 설명이다.

말 4개가 출발해서 모두 도착하려면 윷을 몇 번 던져야 할까? 이걸 구하려면 먼저 한 번 윷을 던졌을 때 얼마나 이동할 수 있는지를 알려주는 기댓값을 알아야 한다. 여기서는 허명회 교수팀이 얻은 경험값을 윷의 확률로 활용한다. 즉 도는 0.2, 개는 0.31, 걸은 0.34, 윷은 0.12, 모는 0.03이라고 가정한다.

윷이 이동하는 칸을 숫자로 바꾸고, 각 확률을 곱한 뒤 이를 모두 더하면 기댓값을 얻을 수 있다. 이때 윷이나 모가 여러번 나올 수 있는데, 이때는 이동하는 칸 수에 비해 나올 확률이 워낙 작아 0에 가까운 값이 된다. 즉 도1×0.2+개2×0.31+걸3×0.34+윷도5×0.12×0.2+윷개6×0.12×0.31+윷걸7×0.12×0.34+모도6×0.03×0.2+모개7×0.03×0.31+모걸 8×0.03×0.34+윷윷도9×0.12×0.12×0.2+… ≒ 2.85다. 한 번 윷을 던지면 2.85칸 이동하는 셈이다.

윷판에는 총 29개의 지점이 있다. 각 지점을 밭이라고도 하며 자리마다 이름이 있다. 말의 이동 경로는 크게 넷이다. 가장 짧은 경로는 앞밭과 방을 지나 12칸을 거쳐 나는 경로다. 뒷밭에서 대각선으로 나는 경로와 앞밭에서 쨀밭을 거쳐 나는 경로는 모두 17칸을 이동하면 된다. 외곽을 따라 가장 길게 도는 마지막 경로는 21칸을 움직여야 난다.
 

그렇다면 4명이 한 경기를 하는 시간은 얼마나 될까? 1번 던지고 말을 움직이는데 평균 20초가 걸린다고 생각하면 4명일경우 4명×20초×24번=1920초=32분이걸린다. 이렇게 계산하면 2명은 16분, 6명은 48분이 나온다. 실제에서는 말을 잡거나 윷이나 모가 나와 더 던지는 경우가 있어 시간이 더 걸릴 가능성이 크지만, 1명이나 3명의 말이 먼저 나서 끝나는 경우 시간이 줄어들 수도 있다.

윷놀이에서 4명이 경기를 할 경우에 한사람에게 예외 규정을 두면 안 된다. ‘전통놀이 삼국대전’ 윷놀이에서 만약 당나라가 자신들의 땅을 모두 걸어야 했다면 결과는 달라졌을 것이다. 셋 이상이 놀이를 할 때는 둘의 협력에 따라 승부가 한쪽으로 쏠릴 수 있다. 따라서 둘씩 짝을 이루거나 꼴찌에게 가혹한 벌점을 줘 모두가 최선을 다하도록 해야 한다.
 

*그래프 이론

윷놀이 말판이나 지하철 노선도처럼 점과 선으로 이뤄진 형태를 수학에서는 특별히 그래프 이론으로 다룬다. 여기서 그래프는 함수그래프나 막대그래프에서 말하는 그래프와는 다른 용어다.


▼관련기사를 계속 보시려면?

Intro. 전통놀이 삼국지
Part 1. 실수가 승부를 가른 고누
Part 2. 기막힌 운이 승리를 가져다준 쌍륙
Part 3. 확률과 전략이 절묘할 때 승리하는 윷놀이