“컷! 꼬꼬~! 그게 아니야! 시청자들은 이제 평범한 착한식당에 질렸다고!”
이영돈PD의 먹거리 X파일 스튜디오에 이상한 손님이 불쑥 찾아왔다. 그 주인공은 바로 치킨맨! 불청객의 등장에 깜짝 놀란 이영돈PD가 말도 못하고 입만 뻐끔거리고 있자, 치킨맨이 당당하게 소리쳤다.
“내가 오늘 새로운 맛을 보여 주지! 이제 착한 식당은 다시 태어난다! 이름하여 <;이영돈PD의 수학 먹거리X파일>;! 꼬꼬~!”
1. 그릇을 검증하라!
수학으로 빚은 소금그릇
아래의 화려한 그릇은 사실 평범한 그릇이 아니다. 이탈리아의 조각가 첼리니의 작품으로, 세계에서 가장 유명한 소금그릇이다. 소금은 16세기까지만 해도 동서양을 통틀어 매우 비싼 식재료였다. 비싼 소금을 식탁에 올려서 마음대로 먹을 수 있는 사람은 왕이나 높은 귀족과 같은 특권 계급뿐이었다. 그래서 서양에서는 예부터 비싼 소금과 어울리는 품격 있는 그릇을 만들어 식탁에 올려 놓았다. 이것이 소금그릇이다.
그런데 소금그릇에 대해 연구한 수학자가 있다. 고대 그리스의 수학자 아르키메데스다. 그가 남긴 <;보조정리집>;에는 모두 15개의 기하학에 관한 정리가 수록돼 있다.
그 중에서 14번째 정리는 다음 도형에 관한 내용이다. 아르키메데스는 이 도형을 ‘셀리논’이라고 불렀다. 셀리논(salinon)은 그리스어로 소금그릇(salt cellar)이라는 뜻이다. 아르키메데스는 <;보조정리집>;의 정리 14번에 소금그릇을 그리는 방법과 소금그릇의 넓이를 구하는 법을 수록해 놓았던 것이다.
이곳은 그냥 평범한 카페 같은데요? 음…, 테이블 위에 놓여진 그릇이 좀 화려하긴 하군요. 하지만 이 식당의 대체 어떤 부분이 특별한지 모르겠습니다.
노노! 그런 평범한 눈으로는 새로운 먹거리 X파일을 찍을 수 없을 걸세. 다시 한번 그릇을 잘 살펴보라고! 뭔가 새로운 냄새가 나지 않나?
좋습니다. 치킨맨 씨와 함께 검증해 보도록 하겠습니다.
소금그릇 그리는 방법
❶ 선분 AB를 지름으로 하는 반원 ACB를 그린다.
❷ 지름 AB 위에 점A와 점B로부터 각각 같은 거리만큼 떨어진 점 D, E를 잡는다.
❸ 선분 AD와 선분 EB를 지름으로 하는 두 개의 반원을 반원 ACB 안쪽에 그린다.
❹ 선분 DE를 지름으로 하는 반원을 반원 ACB와 반대쪽에 그린다.
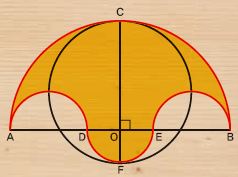
소금그릇의 가장 큰 특징은 소금그릇의 넓이가 선분 CF를 지름으로 하는 원의 넓이와 같다는 것이다. 대체 이 복잡해 보이는 소금그릇의 넓이는 어떻게 구할 수 있을까?

2. 맛있는 역설을 찾아라!
감자는 어디로 간 걸까? 감자역설
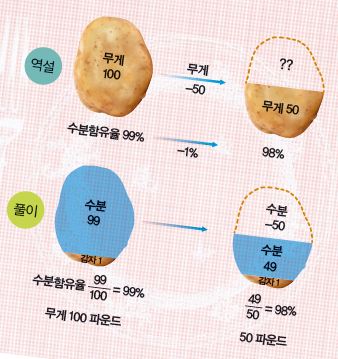
“A가 감자 100파운드를 샀는데, 수분 함유율이 99%였다. 이후 감자가 말라서 수분함유율은 98%가 됐는데, 그 무게는 놀랍게도 50파운드밖에 되지 않았다. 어떻게 된 걸까?”
감자역설로 잘 알려진 이 문제는 영국의 저자 데이비드 달링이 쓴 베스트셀러, <;더 유니버설 북 오브 매스매틱스>;(2004)에 실리며 유명해졌다. 사실 이 문제는 수학에서 말하는 진짜 역설은 아니다. ‘역설’이란 패러독스를 번역한 말로, 그리스어인 Para(반대)와 Doxa(상식적인 견해)의 합성어다. 즉, 역설은 참된 명제와 논증에서 모순된 주장을 나타내는 표현을 말한다. 잘 알려진 역설로 ‘크레타섬의 거짓말쟁이’가 있다.
감자역설은 진짜 역설은 아니지만, 많은 사람들의 상식에서 벗어나는 문제라 역설로 소개됐다. 이 감자는 원래 수분함유율이 99%였는데, 증발 후 수분함유율은 1%밖에 줄지 않았다. 그런데 무게는 절반이나 줄다니, 어떤 비밀이 숨겨진 것일까?
우선 100파운드 감자의 수분함유율이 99%라면 물이 99파운드, 고체의 감자가 1파운드이다. 수분이 증발해도 1파운드의 고체는 증발하지 않으므로, 고체의 감자는 여전히 1파운드다. 그리고 증발이 일어난 뒤 감자의 중량은 50파운드라고 했으므로, 이 중 49파운드는 물이 된다. 따라서 49파운드가 물이고 총 중량은 50파운드이므로, 수분함유율은 98%가 맞다. 즉, 감자역설은 초기에 고체 감자보다 물의 양이 월등히 많다는 걸 생각지 않고 단순히 수치만 비교했기 때문에 역설처럼 느껴질 정도로 기이하게 보이는 것이다.
이 문제를 식으로 쓰면 좀 더 명확해진다. 줄어든 무게를 x파운드로 놓으면, 다음과 같은 식을 세울 수 있다.

그릇의 유래까지 찾아보다니, 과연 새로운 접근이군요. 그나저나 여긴 감자 샌드위치를 파는 카페군요. 치킨맨 씨, 이곳에선 뭘 찾아볼 생각인가요?
흥! 공짜로 알려달라는 건가? 힌트를 주지. 역설로 양념한 감자, 먹어본 적 있나?
양념이 역설이라구요?
샌드위치 정리의 다른 말, 두 경찰관과 술꾼 정리!
‘샌드위치 정리’, ‘압착 정리’, ‘스퀴즈(손가락으로 꾹 눌러 짠다는 뜻) 정리’ 등 다양하게 불리는 이 정리는 고등학교 2학년 함수의 극한에서 배운다.

위 정의에서 함숫값이 어떤 수에 무한히 가까워질 때 ‘수렴한다’고 하고, 그 값을 ‘극한값’이라고 하는 것만 기억해도 좋다. 그리고 샌드위치 정리에서는 그 재료들이 빵 사이에 끼어 있는 것처럼, 어떤 함수가 두 함수 사이에 끼어 있는 성질을 이용해 문제를 해결한다. 직접 구하기 힘든 어떤 함수의 극한값을 구하기 위해, 구하기 쉬운 다른 두 함수의 극한값과 비교하는 것이다.
이탈리아, 중국, 프랑스 등에서는 이 정리를 ‘두 경찰관과 술꾼 정리’라고도 부른다. 두 경찰관이 술에 취한 사람을 양쪽에서 붙잡고 가다가, 감방으로 끌고 들어가는 모습에 빗댄 것이다. 실생활에서 흔히 볼 수 있는 현상이나 음식에 빗대 수학 이론의 이름을 붙인 것이 흥미롭다.
3. 크기도 순서도 엉망진창! 팬케이크 카페의 비밀은?
팬케이크를 순서대로 분류하라!
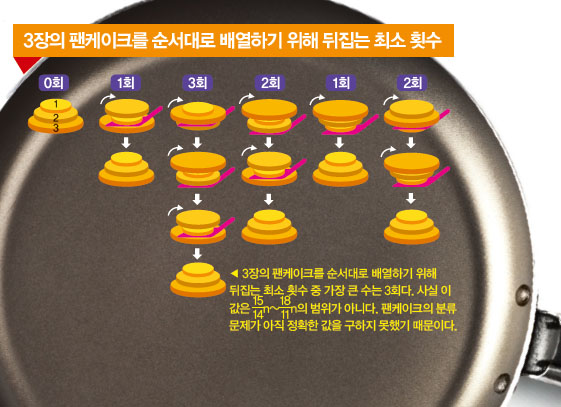
“덤벙대는 요리사가 여러 장의 팬케이크를 주문받아 모두 다른 크기로 만들었다. 웨이터는 엉망으로 쌓인 팬케이크들을 가장 큰 것이 바닥에 오도록 순서대로 배열해 나르기로 한다. n장의 팬케이크를 순서대로 놓으려면 뒤집개로 최소 몇 번을 뒤집어야 할까?”
1975년 미국의 수학자 제이콥 굿맨이 제안한 팬케이크 분류 문제다. 크기 순서대로 놓는 가장 간단한 방법은 처음 뒤집을 때, 가장 큰 팬케이크를 맨 위에 올려놓는 것이다. 두번째에는 가장 큰 팬케이크를 바닥에 갖다 놓는다. 그리고 남아 있는 팬케이크들에 대해 이 작업을 반복한다. 하지만 이 방법은 최소 횟수로 팬케이크를 뒤집는 방법은 아니다.
n장의 팬케이크를 순서대로 배열하기 위한 최소 횟수는 처음 팬케이크가 배열된 순서에 따라 여러 경우의 수(n!)가 나온다. 최소 횟수 중 가장 큰 수는 15/14n~18/11n라고 알려졌지만, 아직 정확한 값은 아니다. 수학자들은 팬케이크를 최소 횟수로 분류하기 위한 더 효율적인 알고리즘을 개발하기 위해 연구하고 있다. 그 중에는 마이크로소프트사의 창업자 빌 게이츠도 있다. 그는 하버드 수학과 출신으로, 1979년 17/16n~(5n+5)/3란 결과를 얻었다.
하지만 2009년 빌게이츠 연구보다 더 정확한 범위가 등장한다. 미국 텍사스대 연구팀이 18/11n번까지 뒤집으면 된다는 사실을 증명한 것이다. 현재까지는 이 증명이 최선이다.
따라서 불쌍한 웨이터는 n장의 팬케이크를 뒤집기 위해 15/14n~18/11n번 사이의 값을 뒤집어야 한다. 만약 팬케이크가 10장이라면, 최소 11번에서 최대 16번만 뒤집으면 순서대로 만들 수 있다.
감자역설을 풀다니 제법이군. 일단 새로운 착한식당의 PD로 합격점이라고 할 수 있겠어.
감사합니다. 엇? 맛있는 팬케이크 냄새가 나는군요. 저도 팬케이크 참 좋아하는데요…. 엥? 이 가게는 왜 이렇게 팬케이크 크기도 제각각이고 순서도 없이 엉망인 상태로 내오는 거죠?
정답! 팬케이크의 제멋대로인 크기와 순서가 이번 착한식당의 열쇠일세.
“아까 그 요리사가 이번엔 팬케이크의 한 면을 홀랑 태우기까지 한다. 크기는 제각각이고 순서대로 놓지 않은 것은 물론이다. 더 큰 곤경에 빠진 웨이터는 타지 않은 면을 위로 해서 나르기로 결심한다. 몇 번을 뒤집어야 탄 면을 모두 아래로 하고, 크기도 순서대로 맞출 수 있을까?”


1995년, 미국의 수학자 다니엘 코헨과 마뉴엘 블럼은 탄 팬케이크를 모두 뒤집기 위해 23/14n번 이하로 뒤집으면 된다는 것을 증명했다.
한편, 팬케이크 문제는(탄 팬케이크 문제 제외) 2011년 NP-hard 문제로 증명됐다. 이는 모든 경우의 수를 전부 확인하는 것 외에 정확한 답을 구할 수 있는 방법이 없는 어려운 문제다.
4. 냅킨 링의 비밀을 풀어라!
냅킨 링에 숨겨진 비밀은?
고급 레스토랑에 가면, 냅킨을 감싸는 고리를 볼 수 있다. 이를 ‘냅킨 링’이라고 한다. 그런데 수학자들은 이 냅킨 링을 보고 수학적인 문제를 생각해 냈다. 바로 ‘냅킨 링 문제’다.
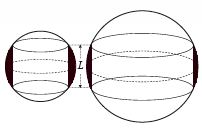
먼저 수학에서 냅킨 링은 ‘스페리컬 링(구 모양의 링)’이라고 불린다. 구에서 원기둥과 위아래 부분까지 제거한 뒤 남겨진 고리의 모습인데, 구의 중심이 뻥 뚫려 있는 재미있는 도형이다.
냅킨 링에는 신기한 성질이 있다. 냅킨 링의 부피가 구의 반지름이 아니라 원기둥의 높이에 의해 결정된다는 것이다. 즉, 아무리 구가 커도 원기둥의 높이만 같으면 냅킨 링의 부피는 같다. 직접 확인해 보자.
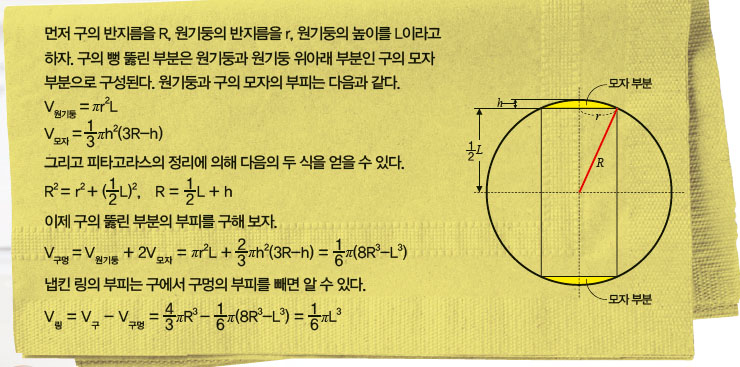
마지막 등식을 보면, 냅킨 링의 부피가 구의 반지름이 아니라 원기둥의 높이에 의해 결정된다는 사실을 확실히 알 수 있다. 이 문제는 17세기 일본 에도 시대의 수학자 세키 코와에 의해 처음 발견됐다. 그는 일본의 뉴튼이라고 불리는 수학자로, 냅킨 링 도형을 가르켜 ‘아크(원호) 링’이라고 불렀다. 미국의 퍼즐 수학자 마틴 가드너는 1959년에 이 문제를 소개하며 ‘믿을 수 없는 문제’라고 부르기도 했다.
이번엔 소시지를 곁들인 브런치 메뉴라…. 벌써 군침이 도는데요? 게다가 냅킹 링으로 잘 싸여진 냅킨까지…. 잘 세팅된 테이블이군요. 그럼 제가 한번 먹어보….
워워~. 그냥 먹을 수야 없지. 자네가 냅킨 링에 숨겨진 비밀을 풀면, 바로 먹게 해 주지.
좋습니다. 그런데 냅킨 링에 대체 무슨 비밀이 숨겨져 있다는 거죠?
맛있는 추측, 소시지 추측
당연하다고 생각한 소시지 모양에도 수학이 숨겨져 있다. 평면에서 원을 포장할 때 어떤 구조로 포장하면 가장 작은 넓이가 나올까? 또, 입체 공간에서 구를 포장할 때 어떤 구조로 포장하면 가장 작은 부피가 나올까?
1975년, 헝가리의 수학자 라즐로 페예즈 토스는 ‘5차원 이상에서는 구의 수가 얼마나 많든지 상관없이 압축포장을 했을 때, 가장 작은 부피를 나타내는 것은 항상 소시지 모양’이라는 소시지 추측을 공식화 했다. 이후 수학자들은 2차원에서는 원, 3차원과 4차원에서는 어떤 조건일 때 어떤 모양으로 포장할 때 최소 부피가 되는지 알아냈다.
그러다가 1998년, 독일의 수학자 울리히 베트케와 마틴 헨크, 외르크 윌스는 42차원 이상이라면 토스의 추측이 옳다는 것을 증명했다. 현재까지는 이 증명이 최선이다. 즉, 5차원~41차원에서는 아직 어떤 구조로 구를 포장해야 가장 부피가 작은지 밝혀지지 않았다.
차원에 따른 최소 포장법
• 2차원일 때 : 원
소시지 : 원 7개를 ‘소시지’ 모양으로 포장하면 넓이를 최소한으로 만들 수 있다. 각 원의 반지름을 1이라고 하면, 소시지의 넓이는 27.141이다.
원 : 원 7개를 육각형으로 배열한 뒤, 가운데 원 하나를 넣으면 넓이가 25.533이 된다. 즉, 소시지 모양으로 배열할 때 보다 넓이가 작다.
• 3차원일 때
소시지(구의 개수≤56개) 구 7개를 될 수 있는 대로 작은 표면적이 나오도록 압축포장을 해 보자. 소시지 모양으로 배열할 때 최소 부피가 나온다. 구가 56개까지는 소시지 모양이 최소 부피가 된다.
구(구의 개수≥57개) 구 57개 이상이면 둥글게 배열할 때 최소 부피다.
• 4차원일 때
소시지(구의 개수≤5만 개) 4차원 구가 5만 개 이상이라면 소시지 모양으로 배열하는 것이 최소 부피를 이룬다. 하지만 10만 개 이상일 경우, 소시지 모양은 최소 부피가 아니다. 몇 개까지 소시지 모양이 최소 부피를 이루는지는 아직 밝혀지지 않았다.
• 42차원 이상
구의 수가 얼마나 많든 소시지 모양으로 포장할 때 최소 부피를 나타낸다.
5. 달콤한 수학을 검증하라!
맛있는 함수, 블라망주 함수
수학자들을 매혹하는 디저트가 있다면, 아마 푸딩일 것이다. 푸딩 중에서도 블라망주는 우유에 과일향을 넣고 젤리처럼 만들어 차갑게 먹는 우유 푸딩의 한 종류다. 이 푸딩을 티스푼으로 살짝 건드리면 양옆으로 불안정하게 기우뚱거리며 사랑스럽게 흔들린다.
그런데 푸딩과 수학자라니 별로 어울리는 조합이 아니다. 하지만 푸딩을 잘라 단면을 살펴보면 매우 수학적인 곡선이 등장한다. 바로 블라망주 함수 곡선이다. 블라망주 함수란 이름은 1980년대 영국의 수학자 데이비드 톨이 곡선의 모양과 블라망주 푸딩의 형태가 닮은 것을 보고 붙인 이름이다.
그런데 왜 이 곡선이 수학자들을 매혹시킨 걸까? 19세기까지 수학자들은 ‘끊어지지 않은 연속함수는 모든 점에서 기울기를 구할 수 있는 미분 가능 함수’라고 생각했다. 그런데 1834년에 연속함수지만 미분할 수 없는 함수가 처음으로 발견됐다. 블라망주 함수는 1903년 일본의 수학자 타카기에 의해 발견된, 연속이지만 미분불가능한 세 번째 함수다.
블라망주 함수는 n값이 커질수록 무한히 많은 작은 뾰족한 점들이 더해진다. 그리고 각각의 뾰족한 점들은 모두 기울기를 갖지 않기 때문에, 어디에서도 미분을 할 수 없다. 수학자들은 이렇게 연속이면서 미분불가능한 함수를 처음 발견했을 때 매우 당황스러움을 느꼈다. 1893년 프랑스의 수학자 샤를 에르미트는 “난 연속 함수이면서 미분불가능한 함수로부터 공포와 증오를 느꼈다”고 말할 정도였다.
어? 어디선가 달콤한 향이 나는군요! 저도 달달한 디저트 참 좋아하는데요, 저 노랗고 투명한 빛깔은 보기만 해도 군침이 돕니다.
이번엔 나도 참 좋아하는 디저트 카페라네. 특히, 블라망주 푸딩에는 수학자들을 매혹시키는 아주 특별한 곡선이 숨겨져 있지.


보너스 마스터 셰프의 비밀은 수학?
수학자가 만든 크림티 스콘, 그 맛은?
영국 셰퍼드대학 수학과의 유지나 챙 박사는 최근 완벽한 스콘을 만들기 위한 ‘크림티 스콘 방정식’을 발표했다. 그녀는 스콘의 지름과 재료의 중량 비율에 따라 수많은 크림티 스콘을 만들며 실험을 했다. 그 결과 가장 맛있는 크림티 스콘을 만들기 위해 크림과 잼의 양을 계산하는 공식을 개발한 것이다.
유지나 챙 박사의 공식에 따르면 스콘의 지름은 4~6cm, 생크림보다는 클로티드 크림(응고된 크림)으로 만드는 것이 좋다. 챙 박사는 스콘이 70g일 때, 잼과 크림은 35g 즉, 스콘: 크림 : 잼 = 2 : 1 : 1의 비율일 때 가장 맛있는 스콘을 만들 수 있다고 제안했다. 이때 잼의 밀도가 크림보다 높기 때문에, 크림 층의 두께는 잼 층보다 두껍다. 따라서 잼을 크림보다 아래쪽에 놓지 않으면 잼이 흘러내려 손에 묻을 수 있으므로, 스콘 바로 위에는 잼을 발라야 한다. 유지나 챙 박사는 스콘 위에 잼과 크림을 얼마나 발라야 할지 그 두께를 계산하는 공식도 알려 주었다. 만약 생크림이라면 응고된 크림보다 푹신하기 때문에 1.5배 더 두껍게 발라야 한다.
크림티 스콘 방정식에 따르면, 스콘과 잼의 가장 맛있는 두께는 스콘의 반지름에 좌우된다. 그럼 수학자가 제안하는 맛있는 스콘의 비밀을 살펴보자.

좋아요. 이제 당신이 말하는 새로운 착한식당의 비밀을 알겠습니다. 비밀은 수학 아닙니까? 그렇다면 치킨맨 씨, 당신은 혹시 수학자인가요?
이제 제 정체를 공개해도 좋을 것 같군요. 저는….
앗! 당신은…?
우유병을 효율적으로 채우려면?

우유와 관련된 재미있는 문제가 있다. 바로 우유 상자 문제다. 한 배달원은 우유병의 개수가 1, 4, 9, …와 같은 제곱수이고, 이들을 정사각형의 상자에 가능한 많이 채우려면 정사각형 배열로 채우는 것이 효율적이라고 확신했다. 병의 단면이 모두 원일 때, 그의 생각이 맞을까?
우유병 36개까지는 그의 생각이 맞지만, 49개 이상부터는 틀리다. 병의 개수가 적으면 벽 가까이에 빈 공간이 발생하는 ‘모서리 효과’가 크게 작용하기 때문이다. 따라서 병들을 상자 벽에 밀착해 정사각형 방식으로 채우는 게 낫다. 병의 개수가 많아지면 모서리 효과보다 병들 사이 공간을 효율적으로 채우는 것이 더 중요하다.
우유병 36개까지는 그의 생각이 맞지만, 49개 이상부터는 틀리다. 병의 개수가 적으면 벽 가까이에 빈 공간이 발생하는 ‘모서리 효과’가 크게 작용하기 때문이다. 따라서 병들을 상자 벽에 밀착해 정사각형 방식으로 채우는 게 낫다. 병의 개수가 많아지면 모서리 효과보다 병들 사이 공간을 효율적으로 채우는 것이 더 중요하다.
17세기 독일의 수학자이자 천문학자인 요하네스 케플러는 작은 입자들의 부피를 최소화하려면 어떻게 배열해야 하는지 연구하다가 직접 일일이 계산해 봤다. 그 결과 정육각형 배열일 때 가장 효율적이라는 사실을 알아낸다. 이를 ‘케플러의 가설’이라고 한다. 케플러의 가설은 1998년 미국의 수학자 토머스 헤일스가 컴퓨터를 활용해 증명했다.
결국 우유병들을 효율적으로 채우려면 49개 이상일 때부터는 정육각형 방식으로 채워야 한다.
결국 우유병들을 효율적으로 채우려면 49개 이상일 때부터는 정육각형 방식으로 채워야 한다.