d라이브러리

대회시작 2시간 전
곱셈 왕 선발대회가 열리다!

곱셈 왕 선발대회는 한 여학생이 보낸 편지로부터 시작됐습니다.

"저는 올해 초등학교 3학년이 된 공세미에요. 두 자리 수의 곱셈을 배우고 있는데, 2학년 때 외우지 못한 구구단 때문에 곱셈이 너무 어려워요. 덧셈은 쉬운데…. 이게 다 알콰리즈미 할아버지 때문이에요. 구구단을 외우지 않고도 곱셈을 할 수는 없을까요?"

휴…, 곱셈은 구구단만 잘 외우면 되는 것을…. 솔직히 편지를 받았을 때 저로서는 잘 이해가 되지 않았습니다. 흠흠, 그렇지만 어쩌겠어요. 이런 말은 제 입으로 하면 좀 쑥스럽지만, 제가 바로 사람들이 대수학의 아버지이자 계산방법에 한 획을 그었다고 인정하는 수학자 알콰리즈미 아닙니까? 하하~.

그래서 구구단을 외우지 못해 곱셈이 괴로운 학생들을 위해 특별히 곱셈 왕 선발대회를 열기로 했어요. 이번 대회의 곱셈 왕 선발 기준은 많은 사람들이 쓰는 곱셈법을 사용하지 않고, 참신하고 독특한 방법으로 곱셈을 하는 것입니다.

그럼 최고의 곱셈 왕을 선발하는 곱셈 왕 선발대회의 문제를 지금 공개합니다! 뿅!


곱셈 왕 선발대회 문제

25 곱하기 13을 계산하시오.

어라? 문제가 너무 쉽다고요? 곱셈 왕 선발대회는 답을 맞히는 대회가 아니라 곱셈을 하는 방법, 즉 아이디어를 심사하는 대회입니다. 단, 암산을 하거나 오른쪽 곱셈과 같이 익숙한 곱셈법을 사용하면 실격입니다!
 후보 1 고대 이집트인과 러시아 농부 팀
‘2배 하기’와 ‘더하기’만으로 곱셈을 할 수 있어요!

이 대회는 우리를 위해 준비된 것이나 다름이 없네요. 우리가 소개할 곱셈법은 조~금 번거롭기는 해도, 구구단을 전혀 외우지 않고서도 곱셈을 할 수 있는 놀라운 방법이랍니다. 더하기만으로도 곱셈을 할 수 있다는 점에 주목해 주세요!


고대 이집트 사람들의 곱셈법
 
과정 ➊ 곱셈식에서 앞에 있는 수를 1과 2의 거듭제곱의 합으로 이뤄지도록, 그 수를 찾는다. 즉, 25=1+8+16으로 나타낼 수 있다. 그런 다음 1, 8, 16의 숫자 왼쪽에 ∨로 표시한다.
과정 ➋ 곱셈식에서 뒤에 있는 수 13을 계속 2배씩 해서 나온 값을 차례로 아래에 쓴다.
과정 ➌ ∨표 한 곳에 해당하는 13의 배수 값(13, 104, 208)을 모두 더한 값이 곱셈의 결과다. 즉, 25×13=13+104+208=325이다.

이 곱셈법은 이진법과 분배법칙을 이용한 것이다.
예를 들어 25×13=(1+2³+2⁴)×13=(1+8+16)×13=13+104+208=325와 같이 계산한 것이다.

고대 이집트 사람들의 곱셈법은 크게 두 가지 과정으로 나눌 수 있다. 첫 번째는 곱셈식에서 왼쪽에 위치한 수를 이진법으로 분해하는 것이고, 두 번째는 곱셈식에서 오른쪽에 위치한 수를 ‘2배’ 하는 것이다.

그렇다면 고대 이집트 사람들은 왜 수를 이진법으로 분해했을까? 또 고대 이집트 사람들은 오래 전부터 이진법을 알고 있었던 걸까? 사실 고대 이집트 사람들은 기본적으로 십진법을 썼다. 그러나 경험적으로 모든 수를 1과 2의 거듭제곱의 합으로 나타낼 수 있다는 사실을 알고 있었다. 따라서 곱셈식에서 수를 이진법으로 분해해 ‘2배 하기’와 ‘더하기’만으로도 곱셈을 할 수 있었던 것이다.

러시아 농부들의 곱셈법

고대 이집트 사람들의 곱셈법과 비슷하면서도 조금 다른 러시아 농부들의 곱셈법도 있다. 러시아 농부들의 곱셈법에서는 곱셈식에서 왼쪽에 위치한 수를 2로 나눠 그 몫을 쓰고, 나머지와 상관없이 몫을 연속해서 2로 나눈다. 고대 이집트 사람들의 곱셈법과 조금 다르지만, 본질적으로 수를 2로 분해한다는 점은 똑같다. 결국 러시아 농부들의 곱셈법도 이진법과 분배법칙을 이용한 것이다.
 
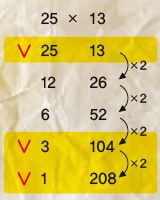
과정 ➊ 곱셈식에서 왼쪽에 있는 수를 연속해서 2로 나눈다. 이때 나머지가 1이 있어도 상관없이 몫을 쓰고, 그 값을 계속 나누면 된다. 몫이 1이 될 때까지 나눈 몫을 써 내려간다.
과정 ➋ 곱셈식에서 오른쪽에 있는 숫자는 2배한 값을 연속해서 써 내려간다.
과정 ➌ 왼쪽 열의 수가 홀수인 경우, 같은 줄에 있는 오른쪽 수들을모두 더한 값이 곱셈 값이 된다. 즉, 25×13=13+104+208=325다. 이 곱셈법에서 왼쪽 열에서 홀수인 수는, 이진법으로 표현했을 때 자릿값이 1인 숫자를 나타낸다.
예를 들어 25를 이진법으로 나타내면 11001₍₂₎인데, 25는 2⁰인 1의 자리를, 3은 2³자리를, 1은 2⁴자리를 뜻한다.

알콰리즈미의 심사평 ★★☆☆☆
정말 구구단을 사용하지 않고도 곱셈을 할 수 있는 독특한 곱셈법이군요. 특히 수를 2의 거듭제곱의 합으로 표현하는 아이디어가 신선합니다. 그런데 곱셈 값을 얻기까지 과정이 좀 길군요. 큰 숫자의 곱셈을 하려면 몇 시간이 걸릴지도 모르겠어요.

후보 2 인도의 바스카라와 존 네이피어 팀
선긋기와 표만 있으면 곱셈도 문제없어요!

이런 말은 안 하려고 했는데, 솔직히 앞 팀의 곱셈법으로 곱셈하다가 졸려서 하품이 났습니다. 아흠~. 저희 팀의 곱셈법은 무척 간단합니다. 선긋기와 표만 있으면 되지요. 특히 선긋기 곱셈은 숫자를 거의 쓰지 않고도 곱셈이 가능합니다. 못 믿는 눈치군요. 그럼 직접 보실래요?

선만 잘 그으면 곱셈이 된다?!
 
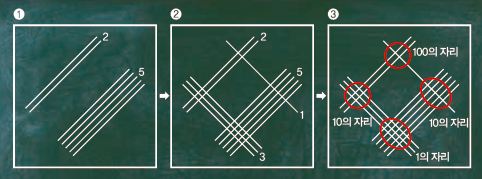
과정 ❶ 25×13을 하려면 우선, 십의 자리 수인 2를 나타내기 위해 선 2개를 인접해서 긋는다. 그런 다음, 2개의 선과 약간 떨어진 곳에 선 5개를 다시 인접해서 긋는다.
과정 ❷ 과정❶에서와 같은 방법으로 13을 선으로 나타낸다. 단, 과정 ➊에서 그린 선과 직각으로 교차하도록 긋는다.
과정 ❸ 교차점을 센다. 100의 자리는 2개, 10의 자리는 6+5=11개, 그리고 1의 자리는 15개로, 모두 더하면 (100×2)+(10×11)+(1×15)=200+110+15=325다.

선 긋기 곱셈법은 자연수의 곱셈 원리를 잘 활용한 방법이다. 자연수의 곱셈은 덧셈으로 바꿔 나타낼 수 있다. 예를 들어 3 곱하기 5는 3을 5번 더하면 된다. 선긋기에서 교차점의 개수는 자연수를 연속으로 더한 값이 된다.

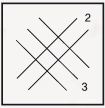
예를 들어 오른쪽 그림과 같이 그은 선에서 교차점은 3+3(또는 2+2+2)으로, 3×2를 나타낸다. 따라서 교차점이 의미하는 자릿수만 알면, 교차점의 개수를 묶은 다음 더하는 것으로 곱셈 값을 쉽게 구할 수 있다.
 
겔로시아 곱셈법과 존 네이피어의 계산막대

표를 사용해 곱셈을 하는 방법에는 겔로시아 곱셈법과, 존 네이피어의 계산막대를 사용한 곱셈법이 있다. 먼저 겔로시아 곱셈법의 ‘겔로시아’는 ‘격자’를 뜻하는 말로, 이 곱셈법은 인도에서 처음 시작된 것으로 추정되고 있다. 인도의 수학자 바스카라가 지은 수학책인 <;릴라바티>;에 등장했고, 또 다른 인도의 수학책에서도 겔로시아 곱셈법이 나타나 있기 때문이다. 겔로시아 곱셈법은 현재 많은 사람들이 사용하는 세로 곱셈법과 원리가 같으며, 사선으로 배열해 수를 더하는 방식이다.

반면 네이피어의 곱셈법은 구구단을 막대로 만들어 곱셈을 쉽게 하도록 만든 것이다. 구구단 계산막대가 있기 때문에 당연히 구구단을 외울 필요가 없지만, 항상 계산막대가 있어야 한다. 네이피어는 계산의 혁명이라고 부르는 ‘로그(log)’를 발명한 수학자로도 잘 알려져 있다.
 
1. 겔로시아 곱셈법
 
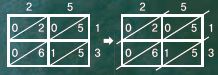
과정 ❶ 격자무늬에 대각선을 그리고, 네모 칸 위와 오른쪽에 곱하는 두 수 25와 13을 쓴다.
과정 ❷ 가로와 세로에 쓰인 두 수의 곱을 대각선으로 나눠진 두 칸에 쓴다.
과정 ❸ 격자무늬에서 사선을 바깥으로 연장한 다음, 사선 안에 있는 수를 더한다. 이때 사선을 따라 더한 결과가 10을 넘으면, 10의 자리 수를 앞의 자리로 올려 준다. 2, 12, 5이므로, 12에서 1을 백의 자리로 올린다. 그러면 (2+1)×100+2×10+5×1=325가 된다.

2. 존 네이피어의 계산막대 곱셈법
 
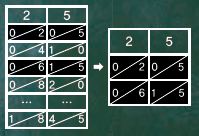
과정 ❶ 곱셈식에서 왼쪽에 해당하는 수의 계산막대를 일렬로 나열한다.
과정 ❷ 곱셈식에서 오른쪽에 있는 수 1, 3에 해당하는 첫 번째와 세 번째 행을 표시한다.
과정 ❸ 사선으로 이어져 같은 곳에 위치한 곳의 수를 더한다. 만약 10이 넘으면 올린다. 여기서는 2, 6+1+5, 5인데, 가운데 수가 12로 10이 넘으므로 1을 앞의 자리로 올린다. 곱셈 값은 325다.

알콰리즈미의 심사평 ★★★☆☆
이 팀의 곱셈법은 정말 쉬우면서도, 구구단을 외우지 않아도 된다는 장점이 있군요. 정말 놀라워요~! 그런데 선긋기 곱셈법 말입니다. 두 자리 수는 괜찮지만, 235×5967과 같은 큰 수를 곱하려면 선을 긋다가 이미 지치지 않을까요? 게다가 겔로시아 곱셈법은 여전히 구구단을 외워야 하군요.

후보 3 러시아의 수학자 카라추바 
큰 수의 곱셈도 문제없어요!

겨우 두 자리 수 곱셈을 하라고요? 제 곱셈법은 큰 수의 곱셈에 유용한 곱셈법인데 말이지요. 컴퓨터에서 제 곱셈 알고리즘을 이용하면, 시간이 훨씬 줄어들어요. 이 점을 꼭 참고해 주세요.

곱셈 알고리즘 등장

카라추바 알고리즘은 러시아의 수학자 아나톨리 알렉세예비치 카라추바가 1960년에 발견한 것으로, 컴퓨터에서 계산을 빠르게 하기 위해 고안된 알고리즘이다.