
“아빠가 웬일이에요? 장미꽃을 다 사오시고?”
“아! 맞다. 아빠, 엄마! 축하드려요~!”
“그런데 그거 아니? 장미의 나뭇잎은 줄기를 세 바퀴 도는 동안 8개의 잎이 달려 있단다. 그런데 신기하게도 여기서 3과 8은 모두 피보나치 수지.”
“장미를 보고 수학을 이야기하다니! 아빠의 수학 사랑은 알아줘야 한다니까~.”
꽃과 함께 피어난 피보나치 수
카라와 입술망초, 물양귀비, 채송화, 코스모스, 금잔화의 공통점은 무엇일까? 누구나 할 수 있는 대답은 ‘꽃’이다. 그런데 정답이 하나 더 있다. 힌트는 꽃잎의 수다. 카라의 꽃잎은 1장, 입술망초는 2장, 물양귀비는 3장, 채송화는 5장, 코스모스는 8장, 금잔화의 꽃잎은 13장이다.
이쯤 되면 눈치챈 독자들이 있을 것이다. 꽃잎의 개수가 모두 피보나치 수 중 하나다. 피보나치 수는 0과 1로 시작하여 앞의 두 수를 더한 값이 다음 수가 되는 특징을 가지고 있다. 0, 1, 1, 2, 3, 5, 8,…과 같이 나타난다.
피보나치 수는 꽃잎뿐만 아니라 식물의 잎차례, 동물의 뿔, 앵무조개 등 다양한 곳에서 살펴볼 수 있다. 이렇게 자연에서 피보나치 수를 쉽게 찾을 수 있는 이유는 피보나치 수의 비가 황금비를 따르기 때문이라는 주장이 있다. 피보나치 수에서 이웃한 두 수 중 더 큰 수를 분자로, 작은 수로 분모로 나타내면 근삿값이 약 1.618로 황금비가 된다. 황금비는 주어진 길이를 가장 이상적으로 둘로 나누는 비로, 약 1:1.618 또는 1:0.618을 의미한다.
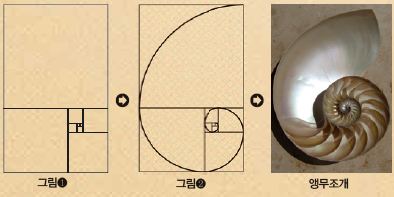
피보나치 수에서 두 번째와 세 번째 수인 1을 한 변으로 하는 정사각형을 그림❶과 같이 나란히 그리고, 네 번째 수인 2를 한 변으로 하는 정사각형을 그린다. 이번에는 다섯 번째 수와 여섯 번째 수를 한 변으로 하는 정사각형을 그린다. 이와 같은 방법으로 정사각형을 그려나간 뒤, 첫 번째 그린 정사각형부터 그림❷와 같이 사분원의 원호를 그려나가면 하나의 아름다운 곡선을 얻을 수 있다. 이것이 바로 ‘황금나선’이다.
앞에서 살펴보았듯이 피보나치 수의 비는 황금비를 이룬다. 이 나선은 황금비를 이루는 정사각형이 모여 만들어졌기 때문에 황금나선이라고 부른다.



아하! 실험 플러스 똑똑한 나선형 잎차례
식물의 잎은 성장에 필요한 햇빛과 물 등을 얻기에 가장 좋은 곳에 생긴다. 잎이 난 자리 바로 위에 입이 나면 아래 잎은 성장에 필요한 요소를 충분히 얻기 힘들기 때문이다. 따라서 대부분 식물의 잎은 줄기를 따라 나선형으로 생긴다. 이렇게 잎이 나는 방식을 ‘나선형 잎차례’라고 한다.

즉 식물이 a번 회전하면서 b개의 잎이 나오고 b+1번째 잎이 처음 잎 위에 나면 a/b잎차례라고 한다. 예를 들어 대나무는 1/2잎차례, 벚꽃은 2/5잎차례다.
그런데 식물의 나선형 잎차례와 피보나치 수의 비율을 나란히 두고 살펴보면 거의 똑같다는 것을 알 수 있다. 나선형 잎차례를 구성하고 있는 수는 모두 피보나치 수이기 때문이다.












