제1코스 15의 다양한 별칭 “삼각수, 메르센 수, 마방진 상수”
15는 당구장에서도 쉽게 발견할 수 있다. 당구의 한 종류인 포켓볼에서는 삼각형으로 15개의 당구공을 모아놓고 경기를 시작하는데, 이 공들을 배치할 때 쓰는 삼각형의 틀을 ‘트라이앵글 랙’이라고 한다. 15개의 공에는 각각 1부터 15까지의 숫자가 적혀 있다.
15는 1+2+3+4+5로 나타낼 수 있다. 1부터 연속한 자연수의 합으로 나타낼 수 있는 수를 *형상수 중에서도 ‘삼각수’라고 한다. 삼각수는 삼각형으로 표현된 수로, 1, 3, 6, 10, 15, …로 배열된다. 15는 삼각수 중 5번째에 해당하는 수다.
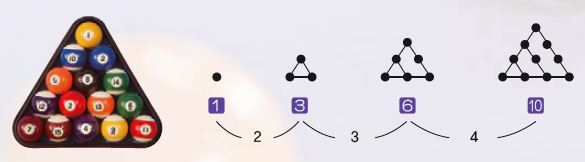


*형상수 고대 그리스 시대의 피타고라스학파는 우주 만물이 수로 이루어져 있다고 믿고 도형을 이용해 숫자를 표현했다. 이렇게 도형으로 묘사된 자연수를 형상수라고 한다.
*메르센 수 2의 거듭제곱에서 1이 모자라는 수. 즉 자연수 n에 대하여 2ⁿ-1꼴의 수.
제2코스 도저히 풀 수 없는 퍼즐, 15퍼즐
15퍼즐은 4×4로 돼 있는 판에 1부터 15까지 흩어져 있는 숫자들을 순서대로 정렬하는 퍼즐이다. 이 퍼즐은 퍼즐 작가로 유명한 미국의 샘로이드가 1부터 13까지는 차례대로 배치돼 있으면서 14와 15의 자리만 바뀌어 있는 퍼즐을 푸는 사람에게 1000달러(현재 가치로 환산하면 약 1억원에 해당하는 금액)의 상금을 걸며 유명해졌다. 하지만 상금을 얻은 사람은 아무도 없었다. 왜냐하면 15퍼즐이 갖고 있는 어떤 특징으로 인해, 14와 15만 뒤바뀐 상태에서는 아무리 노력해도 숫자들을 차례대로 되돌릴 수 없기 때문이다.
그럼 15퍼즐이 갖고 있는 특징에 대해 알아보자. 4×4 퍼즐의 왼쪽에서 오른쪽으로, 위에서 아래로 갈수록 자릿값이 커진다고 생각해 보자. 퍼즐에 배열된 숫자 n마다, 자신보다 자릿값이 큰 위치에 있으면서 크기가 작은 숫자는 몇 개인지 세어 보고 이 값을 f(n)이라 하자.
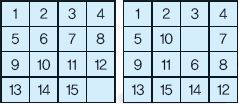
예를 들어 첫 번째 퍼즐은 모든 숫자가 순서대로 배열돼 있기 때문에, 각 숫자에 대해 자신보다 자릿값이 큰 위치에 있는 숫자는 모두 해당 숫자보다 크다. 따라서 f(1)=f(2)=…=f(15)=0이므로 f(1)+f(2)+…+f(15)=0이다.
f(1)+f(2)+…+f(15)의 값을 X라 하고, 두 번째 퍼즐의 X값을 구해 보자. 두 번째 퍼즐에서 10보다 자릿값이 큰 숫자들 중 7, 9, 6, 8은 10보다 작다. 즉, f(10)=4이다. 1, 2, 3, 4, 5는 자릿값이 큰 숫자들이 모두 자신보다 크므로 f(1)=f(2)=…=f(5)=0이다. 같은 방법으로 f(7)=1, f(9)=f(11)=2, f(6)=f(8)=0, f(13)=f(14)=1, f(15)=2임을 알 수 있다. 따라서 X=13이다.

이제 퍼즐의 빈칸을 기준으로 위, 아래, 양 옆에 있는 숫자들이 이동하면 X값이 어떻게 변하는지 보자. 왼쪽 그림과 같이 3행 2열에 빈 칸이 있으면, 이동할 수 있는 숫자는 빈칸의 위와 아래에 있는 F, M과 양 옆에 있는 I, J다. 이때, I를 빈칸으로 이동해도 f(I)의 값은 변하지 않는다. 따라서 X 값은 변하지 않는다. 이것은 J를 빈칸으로 이동해도 마찬가지다.
이제 F를 이동시켜 보자. F보다 자릿값이 작은 A~E와, F가 이동하려는 칸보다 자릿값이 큰 J~O는 f($n$)의 값이 변하지 않는다. 따라서 변할 가능성이 있는 F, G, H, I의 대소 관계를 4가지로 나눠 f($n$)의 값을 살펴보자.(다음 페이지 표 참고)
모든 경우에서 X값은 홀수만큼 증가하거나 감소함을 알 수 있다. 같은 방법으로 M을 빈 칸으로 이동하는 경우에도 X값이 홀수만큼 증가함을 확인할 수 있다.
1. G, H, I가 모두 F보다 작을 때
F가 G, H, I보다 크므로 f(G), f(H), f(I)는 변하지 않는다. 그러나 f(F)의 값을 살펴보면 G, H, I가 F보다 작으면서, F보다 자릿값이 작은 위치에 있게 되므로 f(F)는 3만큼 줄어든다. 따라서 X의 값은 3만큼 감소한다.
2. G, H, I 중 1개만 F보다 작을 때
G, H, I 중 어느 것이 F보다 작더라도 X의 값의 변화는 마찬가지다. 따라서 G, H, I 중 G가 F보다 작다고 가정하면 f(G) 값은 변하지 않는다. 하지만 H와 I의 경우, 자신보다 자릿값이 큰 위치에 자신들보다 작은 숫자인 F가 있으므로, f(H), f(I)의 값은 1씩 증가한다. 또한 F가 G보다 자릿값이 큰 자리로 이동했기 때문에 f(F)의 값은 1만큼 줄어든다. 따라서 X의 값은 1만큼 증가한다.
3. G, H, I 중 1개만 F보다 클 때
G, H, I 중 어느 것이 F보다 크더라도 X값의 변화는 마찬가지다. 따라서 G, H, I 중 I가 F보다 크다고 가정하면, f(I)의 값은 F가 I보다 작으므로 1 증가한다. 또 , f(G), f(H) 값은 변하지 않는다. 또한 F는 자신보다 작은 G, H가 F의 앞에 위치하게 되므로 f(F) 값은 2만큼 감소한다. 따라서 X값은 1만큼 감소한다.
4. G, H, I가 모두 F보다 클 때
f(G), f(H), f(I)는 G, H, I보다 작은 F가 자신보다 자릿값이 큰 자리로 이동했기 때문에 1씩 증가한다. f(F) 값은 변하지 않는다. 따라서 X값은 3만큼 증가한다.
정리하면, I나 J를 이동한 경우에 X값은 변하지 않으므로 X의 변화량은 0이다. 그리고 빈 칸이 위치한 가로줄은 여전히 3행이므로, 행의 변화량도 0이다. 이때 빈 칸이 위치한 행의 수를 Y라 하면 X의 변화량과 Y의 변화량의 합은 0, 즉 짝수인 것을 알 수 있다.
또한 F나 M을 이동하면 X의 변화량은 홀수다. 3행에 있던 빈칸이 2행이나 4행으로 옮겨지므로 Y의 변화량은 -1 또는 1로 홀수다. 홀수와 홀수의 합은 짝수이므로 X와 Y의 변화량의 합은 짝수다. 결국 15퍼즐은 빈 칸을 중심으로 전, 후, 좌, 우 어디에서 움직이더라도 X, Y의 변화량의 합이 짝수라는 특징을 갖는다.
이제 샘로이드의 15퍼즐의 X+Y의 값을 알아보자. f(1)+f(2)+…+f(14)=0이고, 15 뒤에 14가 있으므로 f(15)=1이다. X=1이고 빈 칸이 4행에 있으므로 Y=4, X+Y=5로 홀수다. 그런데 15퍼즐은 아무리 움직여도 X와 Y의 변화량의 합이 짝수라는 특징을 갖기 때문에, 14와 15가 뒤바뀐 상태의 X+Y가 홀수(5)라면, 퍼즐을 움직인 뒤 X+Y의 값도 홀수여야 한다. 하지만 1부터 15까지 순서대로 놓여진 경우 X=0, Y=4이므로 X+Y=4이다. 즉, 샘로이드의 15퍼즐은 아무리 움직여도 정답 모양으로 만들 수 없다. 따라서 이 퍼즐은 절대로 풀 수 없다.
제3코스 15와 하노이 탑
판 위에 3개의 막대 A, B, C가 고정돼 있다. 첫 번째 막대 A에는 지름이 서로 다른 4개의 원판 중 가장 작은 것이 가장 위에 오고, 가장 큰 것이 가장 아래 오도록 순서대로 놓여 있다. 이 원판을 모두 세 번째 막대 C로 옮기려고 할 때, 필요한 원판의 최소 이동 횟수는 얼마일까? 단,
어떤 경우에도 크기가 작은 원판이 큰 원판보다 아래에 위치할 수는 없다.
이것은 19세기 프랑스 수학자 루카스가 제시한 ‘하노이 탑’이라고 불리는 유명한 수학문제다. 신기하게도 하노이 탑 문제는 원판의 개수가 k개일 때, 원판의 최소 이동 횟수가 항상 ${2}^{k}$-1이 된다는 사실이 알려져 있다. 따라서 위의 문제처럼 원판이 4개인 경우 최소 이동 횟수는 15=2⁴-1이 된다. 이때, 15번만에 원판을 이동하는 과정은 아래 표를 통해 확인할 수 있다.
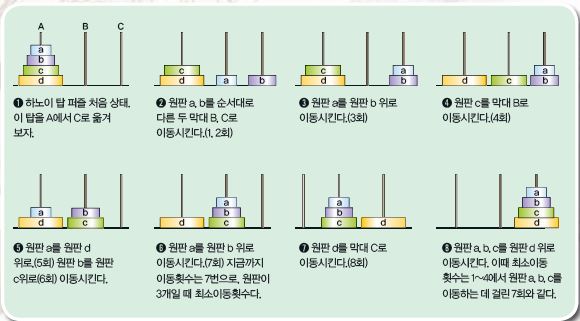
하노이 탑에서는 크기가 작은 원판이 큰 원판보다 아래에 위치할 수 없다는 규칙 때문에, k+1번째로 큰 원판을 이동하려면 먼저 k개의 작은 원판을 이동해야 한다. 즉, 원판 4개를 이동하는 최소 이동 횟수는 7(원판이 3개일 때 최소이동횟수)+1+7(원판이 3개일 때 최소 이동횟수)=15회다.
따라서 k개의 원판을 이동하는 데 필요한 최소 이동 횟수를 f(k)라 하면, 다음 과정을 통해 f(k+1)를 구할 수 있다.
1. k개의 작은 원판을 막대 B로 이동시킨다.(최소 이동 횟수는 f(k))
2. k+1번째로 큰 원판을 막대 C로 이동시킨다.(최소 이동 횟수는 1번)
3. 다시 k개의 작은 원판을 막대 C로 이동시킨다.(최소 이동 횟수는 f(k))
이 과정에서 다음과 같은 식을 세울 수 있다.
f(k+1)=f(k)+1+f(k)=2f(k)+1
f(k+1)+1=2f(k)+1+1=2(f(k)+1)
f(k+1)+1=2(f(k)+1)로부터 f(2)+1은 f(1)+1의 2배, f(3)+1은 f(2)+1의 2배가 된다는 걸 알 수 있다. 즉, f(k+1)+1은 f(k)+1보다 항상 2배씩 커진다.


지금까지 15퍼즐, 마방진, 하노이 탑 등 다양한 퍼즐과 삼각수, 메르센 수 등을 통해 특징이 없을 것만 같던 숫자 15 속에 숨겨진 다양한 매력들을 살펴봤다. 우리의 일상도 매일 반복돼 지루할 때가 있지만, 조금만 생각을 바꾸면 숫자 15처럼 다양한 매력과 즐거움을 찾을 수 있을 것이다. 8월에 만난 숫자 15를 떠올리며 방학을 알차게 마무리하자.