d라이브러리

유리수는 분자와 분모가 정수인 분수 꼴로 나타낼 수 있는 수를 뜻합니다.

유리수에는 자연수와 정수는 물론이고, 소수점 아래 몇 번째 자리에서 끝나는 유한소수도 포함되지만 논의에서 제외합시다. 위질문은 0.3434…와 같이 소수점 아래에서 끝나지 않는 무한소수인 유리수는 반드시 34와 같이 적당한 수가 계속 반복되는가라는 질문입니다.

결론부터 말하자면 그렇습니다. 이유는 다음과 같지요. 유리수는 분수 꼴로 나타낼 수 있으므로 나눗셈을 할 수 있습니다. 유리수를 소수로 나타내는 것은 분자를 분모로 나눠 몫을 써 내려가는 것이지요.
 

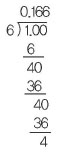
예를 들어 유리수 1/6은 1을 6으로 나누는 것을 생각하면 됩니다. 나눗셈을 하면1/6=0.1666…이라는 것을 알 수 있습니다. 그러니 유리수를 소수로 나타낼 때 반복되는지 아닌지는 나눗셈을 생각했을 때 몫을 보면 알 수 있습니다.

그러면 몫은 어디서 나오는 걸까요? 오른쪽 나눗셈을 보면 나머지가 4로 나왔을 때 몫이 6입니다. 그런데 다시 나머지가 4가 나와서 몫이 또 6이 되지요. 이렇게 나머지가 반복되기 때문에 몫도 반복됩니다.

결국 유리수를 나눗셈으로 생각했을 때 나머지가 반복되면 그때부터는 몫도 반복돼 소수로 나타낸 숫자가 반복된다는 것을 알 수 있습니다. 그런데 중요한 것은 나머지는 나누는 수보다 작다는 사실입니다. 100으로 나누면 나머지는 0부터 99까지의 수만 될 수 있고, 7로 나누면 나머지는 0부터 6까지의 수만 될 수 있습니다.

이렇게 나머지가 될 수 있는 수가 정해져 있기 때문에 몇 번 나눈 다음에는 이미 나왔던 나머지가 반복될 수밖에 없지요. 그 결과 소수로 나타낸 숫자도 반복되는 겁니다. 따라서 유리수를 소수로 나타내면 순환마디가 아무리 길더라도 결국은 순환소수가 됩니다.