d라이브러리

노벨상 중 과학분야 상을 자세히 들여다보면 수학을 쉽게 만날 수 있다. 노벨상을 수상한 연구의 중심에 수학이 있기 때문이다. 수학은 어떤 연구에서는 배경으로, 어떤 연구에서는 핵심으로 역할 했다.수학의 도움이 없었다면 노벨과학상은‘팥 없는 찐빵’신세일지도 모른다.

엉뚱한 연구를 노벨화학상으로 이끈 펜로즈 타일
 

10월 5일 노벨위원회는‘준결정’을 발견한 다니엘 셰흐트만 이스라엘공대 교수를 올해 노벨화학상 수상자로 선정했다. 그가 1982년에 준결정을 발견해 기존의 고체구조에 대한 이해를 근본적으로 바꿔놓았기 때문이다.

결정은 일정한 구조가 반복된 상태의 물질을 말한다. 이때 3각형, 4각형, 6각형 구조만 반복될 수 있다. 그런데 미국 국립표준기술연구소(NIST)에서 박사후과정을 밟고 있던 셰흐트만은 전자현미경으로 알루미늄과 망간 합금을 연구하다가 합금의 구조를 알려주는 전자의 회절패턴이 10각형 모양으로 나타나는 걸 발견했다. 이론과 다른 결과에 그는 실험을 계속했다. 하지만 합금이 5각형 대칭구조라는 사실만 확실해졌을 뿐이다. 수학적으로 10각형이나 5각형은 규칙적인 반복구조를 만들 수 없다. 셰흐트만 박사가 이 실험결과를 다른 동료들에게 말하자 다들 말도 안 되는 얘기라며 엉뚱한 연구로 취급했다. 실험실 책임자는 그에게 결정학 교과서를 건네기도 했다. 심지어 그는‘헛소리하는 사람’으로찍혀 실험실에서 떠나 달라는 얘기까지 들었다. 그가 쓴 논문도 계속 거부당했다.

이런 어려움에서 그를 구해준 것은 펜로즈 타일과 그를 알아준 과학자였다. 그는 저명한 물리학자인 존 칸의 도움을 받아 1984년 저명한 물리학 저널인‘피지컬 리뷰 레터스’에 논문을 게재할 수 있었다. 그리고 한 달뒤 물리학자 폴스타인하르트와 도브 르바인이 펜로즈 타일을 3차원 공간으로 확장해 5각형 대칭구조를 설명한 논문을 발표했다. 합금의 결정 패턴이 펜로즈 타일과 유사하다는 이 논문에서 이들은 좁게보면 패턴이 보이지만 크게 보면 규칙적으로 반복되지 않는 이런 구조를 준결정이라고 이름 붙였다. 결국 1992년에 열린 국제결정학총회에서 결정에 대한 정의가 바뀌고, 고체에 준결정이라는 새로운 형태가 추가됐다.

펜로즈 타일이 있었기에 셰흐트만 박사를 황당하게 바라보던 시선을 바꿀 수 있었다. 셰흐트만 교수가 발견한 구조가 준결정으로 인정받은 데는 수학이 큰 역할을 한 셈이다. 그런데 펜로즈 타일은 어떤 걸까? 부엌이나 화장실, 방의 벽면이나 바닥을 볼 때마다 비슷한 모양이 반복되는 것을 발견할 수있다. 보통은 정사각형이나 직사각형의 모양이 규칙적으로 바닥이나 벽면을 꽉 채운다. 이렇게 빈틈없이 타일을 까는 과정을 타일링이라고 한다. 주변에서 흔히 볼 수 있는 타일링 대부분은 주기적 타일링 방식으로 만들어진다. 어떤 지점의 타일링 패턴을 그대로 옮겨 다른 위치에 놓았을 때 겹쳐지면‘주기적 타일링’, 겹쳐지지 않으면‘비주기적 타일링’으로 구분한다.
 

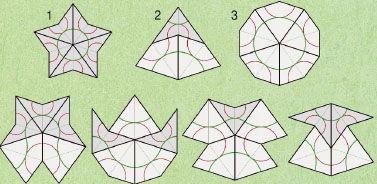
주기적 타일링과 비주기적 타일링의 종류는 무궁무진하다. 주기적 타일링의 경우 수학자들이 타일 모양은 똑같지 않아도 타일링의 구조가 본질적으로 같은 경우를 한 그룹으로 묶었더니 모두 17개 그룹이 되는 걸 알아냈다. 즉 어떤 모양도 주기적 타일링이라면 17개 그룹 중 하나라는 얘기다. 반면 비주기적 타일링은 타일의 모양을 모두 다르게 하면 본질적으로 모두 달라져 한 그룹으로 묶을 수 없다.그만큼 타일링의 종류도 무한정으로 늘어난다. 그런데 몇 개의 타일만으로 반복되지 않는 비주기적 타일링을 만들 순 없을까? 1960년대까지만 해도 수학적으로는 이것이 불가능하다고 알려졌다.

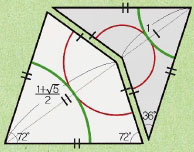
1974년 영국의 이론물리학자이자 수학자인 옥스퍼드대 로저 펜로즈 교수는 취미로 이런 조건을 만족시키는 타일의 개수를 찾다가 획기적인 타일링을 발견했다. 단 2종류의 타일만으로 규칙적이지 않은 타일링을 만들어낸 것이다. 오늘날‘펜로즈 타일링’이라고 불리는 묶음 중 하나인데, 연(kite)과 다트(dart)라고 불리는 타일로 구성된다. 펜로즈 타일링은 자세히 들여다보면 같은 패턴을 쉽게 찾을 수 있다. 하지만 전체적으로 보면 주기적으로 반복되지 않는다. 즉 어떤 모양을 떼어서 옮겨도 다른 자리와 겹쳐지지 않는다.
 

노벨상의 바탕은 수학
 

인체 내 세포 면역체계가 병원체를 어떻게 인식하고 파괴하는가에 대한 메커니즘 연구로 1996년 노벨생리의학상을 받았던 피터 도어티는‘노벨상 가이드’라는 책의‘노벨상을 받는 법’에서 순수 수학은 수상 대상에 없지만 물리학과 경제학의 중심에는 수학이 있다고 말했다. 물리학과 경제학 분야에서 노벨상을 탈 정도의 연구를 하려면 기본적으로 수학을 배경으로 한 이론을 활용하기 마련이라는 설명이다.

실제 많은 노벨상 연구에서 이런 특징을 발견할 수 있다. 노벨경제학상의 경우 대표적인 사례로 꼽히는 것이 1994년 존 내시의 수상이다. 그는‘내시 균형’이라 알려진‘비협력 게임이론’으로 경제학상을 받았다. 바둑과 장기 같은 게임에서 내가 어떤 행동을 하면 이에 따라 상대방의 행동이 달라지는데, 이것을 수학적으로 체계화한 것이 게임이론이다.

내시 균형은 실제 경매나 각종 경제 주체들의 활동에서 만날 수 있다. 석유수출국기구(OPEC)에서 석유를 적게 생산해 수출하면 석유 가격이 올라간다. 그러면 그만큼 이익률이 높아지는데, 각 나라마다 다른 나라를 믿지 못하고 다른 나라가 덜 생산하는 동안 자신이 더 생산해서 더 많은 이익을 얻으려 한다. 결국 모든 나라가 석유를 약속보다 더 생산하게 돼 석유 가격은 떨어지게 된다. 이렇게 대부분의 경제활동이 내시 균형 상태에 이르는 이유는 현실적인 선택에서 이 상태에 있을 때가 가장 안정적이기 때문이다.

노벨물리학상에서도 수학의 힘을 만날 수 있다. 2008년 미국 시카고대 남부 요이치로 교수는 입자 세계에서 자발적으로 일어나는 대칭성 깨짐을 수학적으로 정리한 업적으로 물리학상을 공동수상했다. 남부 교수는 기본입자들이 상호작용으로 대칭성이 스스로 깨지는 구체적인 모형을 최초로 찾아냈다. 그리고 이때 질량과 스핀이 0인 입자가 나타난다는 사실을 수학적으로 입증했다. 그런데 대칭성이 자발적으로 깨진다는 게 어떤 뜻일까?

예를 들어 돌고 있는 팽이는 쓰러지기 전까지 팽이 축을 기준으로 원형 대칭성이 있다. 그리고 모든 방향으로 쓰러질 확률도 같다. 하지만 팽이가 쓰러지고 나면 다른 방향으로 쓰러질 가능성은 사라지고 팽이가 쓰러진 방향만 선택된다. 결국 대칭성이 깨진다. 즉 팽이의 에너지가 낮은 상태가 되면 대칭성도 줄고 결국에는 깨진다는 얘기다.

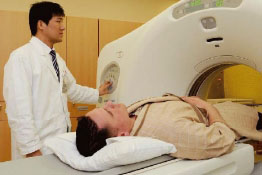
따로 공부한 수학적 지식이 노벨상에 기여한 경우도 있다. 앨런 코맥은 1979년 컴퓨터를 이용한 X선 단층촬영기술(CT)을 개발한 업적으로 노벨생리의학상을 공동수상했다. 물체가 겹쳐 보이는 일반 X선 사진에 비해 CT는 김밥을 썰듯 몸속 단면의 모습을 찍을 수 있다. 가슴과 배는 물론 전립선이나 자궁,난소 등을 촬영할 때 많이 이용된다. 그는 음악을 즐기면서 좋아하는 천문학을 잘 알려는 욕심으로 혼자서 수학과 물리학을 공부했다. 이때 익힌 수학이 컴퓨터 단층촬영기술의 원리를 밝히는 데 큰 도움이 됐다고 한다.

한편 수학책이 노벨상의 길로 인도하기도 했다. 1995년 노벨물리학상을 받은 마틴 펄은 도서관에서 ‘백만인의 수학’같은 책을 읽고 과학자가 되기로 결심했다고 한다. 백만인의 수학은 당시 미국에서베스트셀러였다.

이처럼 과학 분야 연구에서 수학적인 증명이나 수학적인 기여가 노벨상 수상까지 이어지는 이유는 간단하다. 어떤 현상을 간단한 식으로 나타내거나 수학으로 증명했다는 것은 우리가 자연을 더 쉽게 이해할 수 있게 돕고, 확실하게 알게 됐다는 것을 의미하기 때문이다. 실험으로 얻은개별적인 결과 값은 큰 힘을 가지지 못하지만 이것이 수학의 도움을 얻어 체계적으로 정리되면 큰 힘을 발휘할 수 있다.
 

X note
죄수의 딜레마

비협력 게임이론을 이야기할 때 드는 대표적인 예다. 두 명의 범인이 있다. 각각에게“만약 당신이 자백하고 상대가 자백하지 않으면 당신은 풀려나고 상대는 감옥에서 10년을 보내야 한다. 하지만 상대가 자백하고 당신이 자백하지 않으면 반대가 된다. 만약 둘 다 자백한다면 각각 5년을 감옥에서 보내게 되고, 둘 다 자백하지 않으면 각각 1년을 감옥에서 보내야 한다”고 말한다. 이때 죄수들은 어떤 선택을 할까? 이들에게 가장 합리적인 선택은 둘 다 자백하지 않아 1년 동안 감옥에서 보내는 것이다. 하지만 상대방을 서로 믿을 수 없다는 문제가 생긴다. 즉 자신이 자백하지 않았는데 상대방이 자백할 경우를 고려할 수밖에 없다. 결국 상대방이 자백할 것이라는 가정에서(상대방을 배신해서) 둘다 자백하는 것이 현실적인 선택이 된다. 이런 선택이‘내시 균형’상태다.


▼관련기사를 계속 보시려면?

INTRO. 수학 연구, 재미있거나 의미 있거나
PART 1. 황당한 이그노벨상, 알고 보면 의미심장해 
PART 2. 노벨상을 부르는 수학의 힘