

각하는 편이다. 곡면 두 개를 더하려면 양쪽에서 원반을 하나씩 잘라낸 다음, 새로 생긴 경계선을 따라서 붙이면 된다.(그림❶)
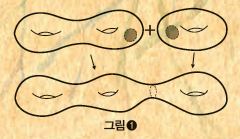
20세기 후반 정보 과학의 발전에 크게 기여한 ‘반도체 곱셈’이란 연산도 있다. 반도체는 전류가 흐르는 상태(C)와 흐르지 않는 상태(N)로 두 가지가 가능해, 다양한 상태의 반도체 메모리 셀을 수 없이 배열하며 정보를 저장한다. 우리가 쓰는 글이나 사진, 동영상 등이 모두 CCNNCNC… 꼴로 저장되는 것이다.
그런데 놀라운 것은 반도체의 기이한 연산이 아주 유용하다는 것이다. 반도체 덧셈의 정의는 다음과 같이 무척 간단하다. 이 때문에 긴 반도체열도 자연스럽게 확장된다.
N+N=N, N+C=C, C+C=N
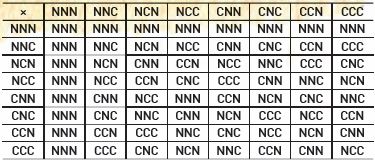
가령 CCC+CNC를 계산하면 각 자리를 따로 더해서 NCN을 얻는다. 수의 덧셈보다 훨씬 쉽다. 그런데 곱셈은 꽤 복잡하다. 표를 보면 (CCN)¹=CCN, (CCN)²=NCN, (CCN)³=CCC, (CCN)⁴=CNN…과 같이 나온다. NNN만 빼고 나머지 원소들은 다 CCN 하나의 거듭제곱으로 표현된다. 이러한 성향은 훨씬 긴 메모리 셀에서도 반복되어 정보의 저장이나 전송에 큰 도움이 된다.
입자의 연산
이번호에서 정말 이야기하고 싶은 것은 ‘입자의 연산’이다. 그중 가장 중요한 예 하나를 그림을 통해 보여 주자면 다음과 같다.
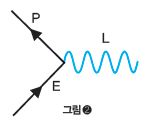
그림❷는 양자(P)와 전자(E)가 부딪혀서 서로 소멸되고 광자(L), 즉 빛을 발하는 과정을 나타낸다. 이 과정을 연산기호 *로 나타내면 (양자)*(전자)=(광자) 꼴의 등식이 성립한다. 여기서 연산 *는 곱셈으로 해석하는 것이 옳다. 왜일까?
우선 입자의 덧셈은 이미 따로 정해져 있다. 양자역학에서는 입자 덧셈의 가능성을 ‘중첩 원리’라고 부른다. 이것은 서로 다른 입자를 더하는 것이 아니 라 입자 하나의 상태들을 더하는 것이다. 여기서 ‘상태’란 일상에서 사용하는 의미로서의 상태다. 그러니까 같은 전자라 해도 여러 다른 위치에 있을 수 있고 속도나 회전 상태, 운동 방향 등이 다양할 수 있다. 그런데 중첩 원리에 의하면 어떤 물건이든지 A라는 상태와 B라는 상태가 가능하면, 그 두 상태의 덧셈 비슷한 연산이 가능하다는 것이다.
연산한 상태를 A#B라 부르자. 대표적인 예로 이중슬릿 실험을 들 수 있다. 위의 구멍만 열고 왼쪽에서 전자를 발사해서 오른쪽에 도달하는 전자의 상태를 E₁이라 하고, 아래 구멍만 열고 전자를 발사해서 오른쪽에 도달하는 전자의 상태를 E₂라 하자. 그러면 두 구멍을 열고 동시에 열고 실험했을 때 오른쪽 벽에 도달하는 전자의 상태는 어떤 합성 상태, 즉 E₁#E₂가 된다.(그림❸)
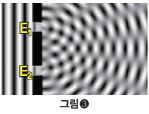
다시 정리하자면 입자 하나의 서로 다른 상태들을 더하는 것이 가능하고, 서로 다른 입자들이 부딪혀서 새로운 입자를 만드는 곱셈도 가능하다.
그런데 어째서 하나는 덧셈 하나는 곱셈이 되는지는 설명하지 않았다. 그 이유는 다음과 같다. 양자와 전자가 만났을 때 나오는 광자의 상태(가령 빛의 색깔)는 소멸된 양자와 전자의 상태에 의존할 것이다. 그러면 다음과 같은 실험을 상상해 보자. 상태가 P인 양자와 상태가 E₁인 전자가 부딪혀서 나온 광자의 상태를 L₁이라하자(P*E₁=L₁). 그 다음 양자의 상태는 그대로 두고 전자의 상태만 바꿔서 실험을 반복하자. 그래서 P인 양자와 상태가 E₂인 전자가 부딪혀서 이번에는 상태 L₂인 광자가 나왔다고 하자(P*E₂=L₂). 그러면 상태가 P인 양자와 상태가 E₁#E₂인 전자가 부딪히면 어떤 광자가 나올까?
그 답은 L₁#L₂ 상태의 광자가 된다. 이것을 수식으로 표현하면 아래와 같은 꼴의 등식이 성립한다.
P*(E₁#E₂)=L₁#L₂=(P*E₁)#(P*E₂)
여기서 강조하고 싶은 것은 이 등식이 완전히 실험적인 사실이라는 것이다. 그런데 보통 수를 다룰 때 분배법칙은 덧셈과 곱셈의 차이를 결정한다. 어떻게 보면 덧셈이나 곱셈이나 두 개를 집어넣었을 때 새로운 수를 만들어내는 과정일 뿐이다. 이 두 과정 사이에 일종의 조화를 표현하는 것이 바로 분배법칙이다.
그런데 분배법칙 안에서 곱셈과 덧셈은 완전히 다른 역할을 한다. 즉 A+(B X C)=(A+B) X (A+C)와 같은 등식은 절대 성립하지 않는다. 그렇기 때문에 위의 식은 우리로 하여금 입자의 두 연산 *와 #을 위에서 설명한 곱셈과 덧셈으로 해석할 수밖에 없게 만든다.
피타고라스의 지혜
‘연산을 할 수 있는 것이 수다’라는 입장을 재검해 보자. 그런데 여기서 이야기하는 연산은 임의적이어서는 안 된다. 우리가 다루는 구조의 자연스러운 원리를 따라야만 한다. 앞서 언급한 연산은 모두 이런 종류의 우수한 연산들이다.
이토록 다양한 연산이 가능하다면 어쩌면 모든 사물에 연산 구조가 있지 않을까 하는 의심이 생길 것이다. 바로 이 생각이 피타고라스의 철학과 직결된다. 모든 사물의 연산이 가능하다면 모든 것이 수라는 뜻이 아닌가! 더구나 사물이 다 입자로 이뤄진 이상, 입자의 연산이 사물의 연산으로 연장되기도 한다.
악기의 음이 여러 주파로 갈라지는 현상을 정확하게 이해하고 있는 현재, 과학자들은 여전히 ‘모든 사물의 이론’을 정립해가고 있다. 지금까지 밝혀진 바에 의하면 사물을 이루는 양자들 역시 기본 주파수로 갈라지고, 서로 다른 주파수 장들의 진동과 상호작용으로부터 현실은 우러나오는 것이다. 그렇기 때문에 우주는 아름다운 음악처럼 조화롭나 보다. 피타고라스의 선견지명이 놀랍지 않을 수 없다.











