네모난 색종이를 가만히 살펴보고 있노라면, 무한한 상상력이 꿈틀댄다. 세상에 많은 것들을 종이 한 장으로 표현할 수 있기 때문이다. 변신의 귀재라 불리는 색종이가 수학 교구로 변신했다! 각도기, 컴퍼스, 자와 같은 도구를 사용하지 않고도 다양한 각을 표현하고 이를 이용해 작품을 만들 수 있다. 어떻게 가능한지 함께 알아보자.
각 15° 만들기
먼저 색종이를 이용해 간단히 확인해 볼 수 있는 각은 90°와 45°다. 정사각형(또는 직사각형) 모양인 색종이의 네 각은 90°이고, 이를 정확히 반으로 접으면 45°이기 때문이다.
그렇다면 15°, 30°, 60°도 색종이로 나타낼 수 있을까? 다음 그림을 함께 살펴보자.
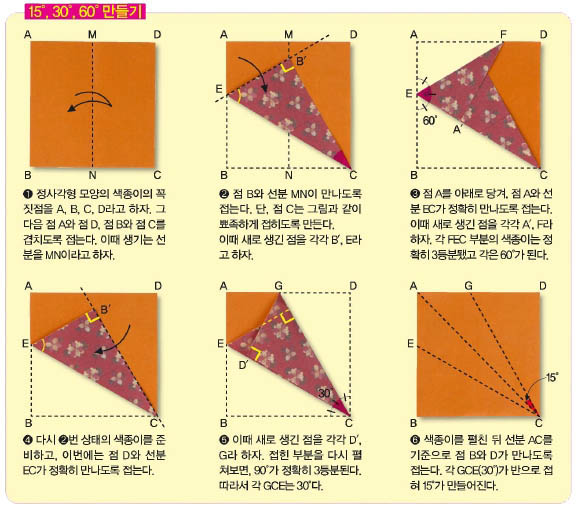
이렇게 접어 만든 각은 모두 정확한 걸까? 어떻게 확인할 수 있을까? 이 활동은 ‘도형의 합동’ 성질 중 ‘직각삼각형은 빗변의 길이와 한 각의 크기가 같으면 합동이다’를 이용해 수학적으로 증명할 수 있다. ❹번에서 삼각형 EBC와 삼각형 EB′C가 합동이다. 왜냐하면 빗변 EC는 접힌 선이므로 길이가 같고, ❸번 또는 ❺번을 통해 보면 직각을 제외한 나머지 한 각의 크기가 같기 때문이다. 물론 각의 크기도 정확하게 구할 수 있다.
또 색종이가 같은 자리에 정확히 포개진다는 것은 포개진 각이 모두 같음을 뜻한다. 덧붙여 색종이는 네 각이 90°인 정사각형이고 접어 만든 삼각형이 직각삼각형이며 삼각형 내각의 합이 180°라는 사실을 이용하면, 만들어진 각을 더욱 명쾌하게 확인할 수 있다.
평면 채우기를 위한 평행사변형 조각
색종이로 각을 만들어 이것을 수학공부에 어떻게 활용할 수 있을까?
색종이를 이용하면 막연하게 머릿속에 떠오르는 각의 크기와는 달리, 예를 들어 30°의 크기를 눈으로 바로 확인할 수 있다. 다른 각도 마찬가지다.
또한 색종이가 가진 장점을 살려 평면 채우기와 같은 작품을 만들어 볼 수 있다. 이번에는 평면 채우기에 대해 알아보자.
평면 채우기란 틈새가 벌어진 곳이나 포개진 곳 없이 일정한 도형으로 평면을 채우는 것을 말한다. 이는 평면 또는 공간을 완전히 메우는 미술의 한 장르다. 영어로 ‘테셀레이션(tessellation)’이라고 하는데, 숫자 ‘4’를 뜻하는 ‘테세레스’에서 유래한 단어다. 이 용어는 정사각형을 이어 붙여 공간을 채우는 과정에서 생겨났다.
평면 채우기는 우리 생활 곳곳에서 발견할 수 있는데, 욕실의 타일이나 거실의 카펫,벽지나 보도블록에서 볼 수 있다. 평면을 빈틈없이 가득 채우려면, 우선 한 점에 모이는 각의 크기가 언제나 360°가 돼야 한다.
색종이를 이용해 평면 채우기를 하기 가장 쉬운 도형은 색종이 모양 그대로 이용하는 정사각형이다. 그렇다면 종이접기만을 이용해 정삼각형 또는 정육각형을 만들 수 있을까? 이를 위해 기본 도형이 되는 평행사변형 조각을 만들어보자.
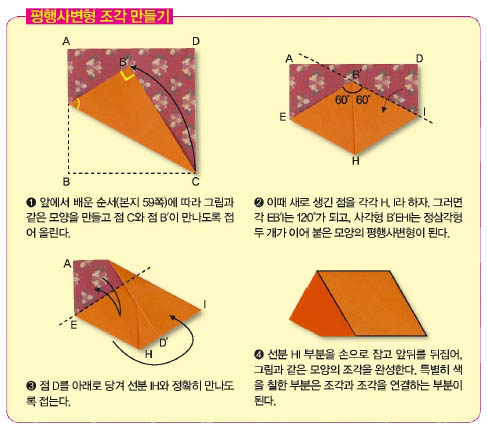
정다각형의 종류와 각의 크기
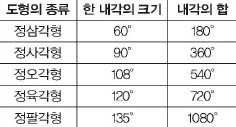
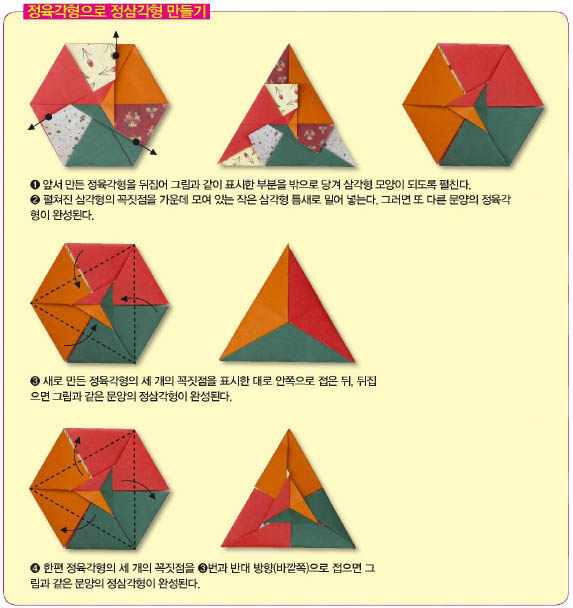
평행사변형으로 정육각형, 정삼각형 만들기
이제 평행사변형 조각을 이용하면 정육각형과 정삼각형을 차례로 만들 수 있다.
먼저, 같은 모양의 조각을 각기 다른 색으로 세 개 만들어 시계 방향으로 이어 붙이면, 정육각형이 완성된다.
서로 다른 세 가지 색을 이용하니 흡사 정육면체처럼 보인다. 이제 정삼각형을 만들어 보자.
오늘 만든 평행사변형 조각과 정육각형, 정삼각형, 그리고 정사각형 색종이를 적절히이용하면 아름다운 평면 채우기 작품을 만들 수 있다. 독자 여러분도 각자의 상상력과 창의력을 듬뿍 담아 자신만의 평면 채우기 작품을 만들어 보길 바란다.