“박사님, 더 이상은 못 가겠어요. 덥고 무겁고 힘들고….”
“조금만 참아라. 저기 보이는 피라미드까지만 가면 정사면체의 비밀을 하나 알려 주마.”
“정사면체의 비밀! 뭔데요? 지금 알려 주시면 안 돼요?”
“허허. 정팔면체와 정사면체를 이용해 피라미드 모양의 거대한 정사면체를 만들려고 한다. 몇 개의 정팔면체와 정사면체가 필요하겠느냐?”
“네? 갑자기 웬 문제예요? 정사면체의 비밀과 관련이 있는 건가요? 풀면 비밀을 알려 주세요.”
정사면체와 정팔면체의 만남
모서리의 길이가 같은 정사면체 4개와 정팔면체 1개를 조합하면 어떤 도형이 만들어질까? 놀랍게도 모서리의 길이가 2배인 정사면체를 만들 수 있다. 정팔면체를 가운데 두고 정사면체 4개를 그림과 같이 붙이면 가능하다. 이 방법을 이용하면 정사면체와 정팔면체의 부피 공식을 몰라도 부피의 비를 알수 있다.
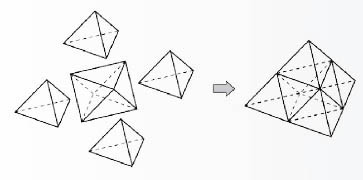
큰 정사면체의 모서리는 작은 정사면체 모서리의 2배이므로 큰 정사면체의 부피는 작은 정사면체의 부피의 8배다. 그런데 큰 정사면체는 정사면체 4개와 정팔면체 1개로 이뤄져 있으므로 정팔면체의 부피는 모서리의 길이가 같은 정사면체 4개와 같음을 알 수 있다. 따라서 정사면체와 정팔면체의 부피 비는 1:4다.
이를 확인하기 위해 정사면체와 정팔면체 부피 공식을 살펴보자.
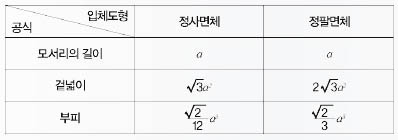
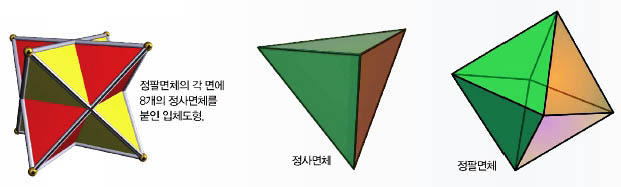
아하! 생각이 쑥쑥!
정사면체와 정팔면체로 만든 7면 입체도형
앞에서 만든 정사면체 병아리를 두 마리 이상 만들어 병아리 경주를 해 보자. 4개의 꼭짓점 중 바닥과 닿는 2개의 꼭짓점을 발이라고 생각하고, 남은 2개의 꼭짓점 중 낮은 높이에 있는 꼭짓점을 머리,높은 부분의 꼭짓점을 꽁무니라고 생각하자.
손가락으로 꽁무니를 살짝 누르듯 밀어 병아리 경주를 해 보면, 병아리가 종종걸음으로 또는 뛰면서나아가는 것을 볼 수 있다. 한 번에 누가 더 멀리 가는지 길이도 재 보자.
모서리의 길이가 같은 정사면체와 정팔면체를 한 개씩 만들자. 면과 면이 꼭 들어맞도록 공유하는 모서리를 테이프로 붙이면 평평한 면이 몇 개인 입체도형이 될까? 면과 면을 붙이면 면 2개가 사라지니까 10개의 평평한 면을 가질 것이라고 추측할 수 있다. 그러나 실제로 두 입체도형을 붙여보면 면 2개가 사라지고 2개씩 이어진 면이 3개가 나타나 평평한 면은 모두 7개인 입체도형이 된다. 즉 7면 입체도형이 생긴다.
여러 가지 입체 도형을 만들어 보고 조합하면서 도형의 성질도 공부하고 새로운 발견도 해 보자. 실험을 통해 수학의 즐거움을 느낄 수 있을 것이다.
◎미션◎
피라미드를 소재로 재미있는 수학 이야기를 만들어 보세요.
평면도형을 가지고 입체도형을 만들라는 수학숙제를 하기 위해 무작정 정삼각형과 정사각형을 많이 만들었어요. 정삼각형과 정사각형을 여러 방법으로 조합해 보다가 정삼각형만을 이용해서 입체도형을만들 수 있겠다는 생각이 드는 거예요. 피라미드를 만들면 되겠더라고요. 먼저 정삼각형 4장을 이용해서 피라미드를 만들었어요. 정삼각형이 너무 많이 남아 4개를 더 만들었죠. 만든 피라미드를 쌓았더니…. 앗! 놀라운 일이 벌어졌어요! 큰 정사면체에 정팔면체 모양의 구멍이 생긴 거예요. 삼각형으로 정사면체와 정팔면체를 모두 표현한 거죠. 제 작품 어떤가요?