d라이브러리

중·고등학교 1학년 수학책의 첫 단원이 무엇인지 아니? 바로 집합이야. 집합을 이용하면 수학에 기본이 되는 수를 주어진 조건에 맞게 나눌 수 있어 그 중요성이 커. 지금부터 집합의 뿌리를 찾아서 떠나 보자. 준비하시고 출발!

 

사람의 피는 A형, B형, AB형, O형으로 나눌 수 있는데 이처럼 주어진 조건에 따라 그 대상을 분명하게 알 수 있는 모임이 집합이다. 노래를 잘하는 사람들의 모임은 집합이 될 수 없는데 사람에 따라 ‘노래를 잘한다’라고 생각하는 기준이 다 다르기 때문이다.
 

집합은 영어로 set라고 한다. set는 고대 영어에서 ‘고정된 장소’, ‘확고하게 고정된’이란 뜻으로 쓰였다. 집합을 이루는 대상 하나하나는 원소라고 한다. 원소는 영어로 element라 하는데 ‘기초’라는 뜻이 있다. 모임을 이루는 기초가 원소라고 생각하면 쉽다.

집합의 대상이 되는 원소를 표현하는 방법에는 두 가지가 있다. 먼저 원소나열법은 {1, 3, 5, 7, 9}처럼 { } 안에 원소를 하나하나 나열하는 방법이다. 조건제시법은 {x|x＜10, x는 홀수}처럼 { } 안에 원소들이 공통적으로 가지는 조건을 적어 넣는 방법이다. 원소나열법은 영어로 listing method라고 하고 조건제시법은 set builder method라고 한다.
 

집합은 원소의 개수에 따라 유한집합과 무한집합, 공집합으로 나뉜다. 유한집합은 {3, 6, 9, 12, 15}처럼 원소의 개수가 유한개인 집합이다. 반대로 원소의 개수가 무한히 많은 집합을 무한집합이라고 한다. 자연수집합, 유리수 집합, 실수집합이 무한집합의 대표적인 예다. 조건에 해당하는 원소가 하나도 없는 집합을 공집합이라고 한다. 예를 들어 15의 약수 중 짝수인 집합은 조건에 해당하는 수가 하나도 없으므로 공집합이다. 공집합은 ‘ø’ 또는 ‘{ }’로 표기한다.

유한집합은 영어로 finite set라고 하는데 finite는 ‘제한하다’, ‘경계를 이루다’를 뜻하는 라틴어 finitus(피니투스)에서 유래했다. 제한된 개수만큼 원소를 가진 집합이라고 생각하면 된다. 무한집합을 뜻하는 영어단어는 infinite set로 finite set에 부정형 접두사 in을 붙여 만든 단어다. 유한집합에 반대되는 의미로 생각하면 쉽다. 공집합은 영어로 empty set라고 한다. empty는 ‘비어 있는’이라는 뜻이 있는데 { }안에 원소가 하나도 없는 집합이라고 생각하면 된다.

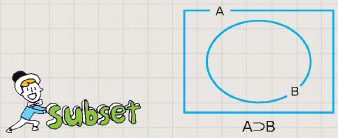
집합 중에는 어떤 집합의 일부분이 되는 집합이 있다. 이를 부분집합이라고 부른다. 예를 들어 살펴보자. 실수집합은 유리수집합과 무리수집합으로 나눌 수 있다. 즉, 유리수집합과 무리수집합은 실수집합에 속해 있다. 이런 유리수집합과 무리수집합을 실수집합의 부분집합이라고 한다. 집합에서는 자기 자신도 부분집합으로 여긴다. 다시 말해 집합 {1, 3, 5}는 {1, 3, 5}의 부분집합이다. 그래서 자기 자신이 아닌 부분집합을 특별히 진부분집합이라고 한다. 예를 들면 {1, 3}은 {1, 3, 5}의 진부분집합이다. 어떤 집합의 부분집합이 되는 관계를 간단히 ‘⊂’나 ‘⊃’로 표기한다.

부분집합을 뜻하는 영어단어는 subset이고 진부분집합은 proper subset이라고 한다. proper는 ‘자신만의 특별한’, ‘적합한’의 의미를 가진 proprius(프로프리우스)라는 라틴어에서 그 어원을 찾을 수 있다.
 

집합도 수처럼 덧셈, 뺄셈을 할 수 있을까? 수를 더하고 빼는 방법과는 조금 다르지만 집합도 연산을 할 수 있다. 지금부터 집합의 연산에 대해 알아보자.

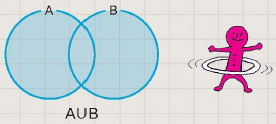
집합도 서로 더할 수 있다. {2, 4, 6}과 {3, 6, 9}를 더하면 {2, 3, 4, 6, 9}가 된다. 즉 집합에서 더하기는 각 집합의 원소를 합하면 되는데 같은 원소가 있을 경우에 원소는 한 번만 쓴다. {2, 3, 4, 6, 9}와 같이 두 집합을 합해 만들어진 집합을 합집합이라고 한다. 집합에서 더하기 기호는 ‘∪’이다. 합집합을 뜻하는 영어단어는 union으로 라틴어의 unio(유니오)에서 왔다. unio는 ‘양파’, ‘진주’, ‘합치다’라는 의미로 사용했다. 여러 겹으로 이루어진 양파, 진주 한 알 한 알이 모여 만들어진 진주목걸이를 생각하면 union의 뜻을 이해하기 쉽다.
 

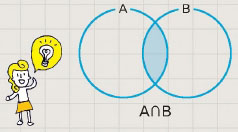
두 집합의 공통된 원소를 나타내는 집합을 교집합이라고 한다. 예를 들어 {2, 4, 6}과 {3, 6, 9}의 교집합은 {6}이다. 교집합의 연산 기호는 ‘∩’이다. 교집합을 뜻하는 영어단어는 intersection이다. intersection은 ‘사이에’, ‘중간에’를 뜻하는 inter와 ‘자르다’를 뜻하는 sect가 합쳐진 단어로 ‘교차 지점’,‘교차로’의 의미도 있다.
 

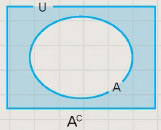
예를 통해 집합의 빼기에 대해 알아보자. {3, 6, 9, 12, 15}에서 {6, 12, 18}을 빼면 {3, 9, 15}다. 집합에서 빼기는 앞에 주어진 집합에서 두 집합의 공통된 원소를 빼는 것이다. 즉 앞에 주어진 집합에서 다른 집합에 포함된 원소를 없애면 된다. 이렇게 빼기 연산을 한 집합을 차집합이라고 한다. 집합에서 빼기 연산은 수의 뺄셈과 같이 ‘-’로 표기한다. 특히 전체집합에서 그의한 부분집합을 뺀 집합을 여집합이라고 한다. 실수집합에서 그의 부분집합인 유리수집합을 빼면 무리수집합이 된다. 다시 말해 실수집합에서 유리수집합의 여집합은 무리수집합이다. 여집합의 기호는 집합 위에 ‘C’를 붙여 나타낸다.
 

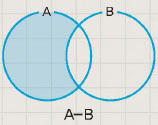
차집합은 영어로 relative complement라고 하고 여집합은 영어로 complement라고 한다.