d라이브러리

Prologue
미국 남북전쟁 때 대포클럽이라는 모임이 생겼습니다. 크고 강력한 대포를 좋아하는 사람들이 결성한 모임이지요. 그런데 전쟁이 끝난 이후 대포의 쓸모가 없어지자 심심해진 회원들이 새로운 생각을 떠올렸습니다. 바로 매우 큰 대포알을 달까지 쏘아 올린다는 것입니다. 심지어는 대포알에 타고 달나라까지 여행하겠다는 사람도 등장하는데….

존경의 법칙

가입 희망자는 신형 대포를 고안하거나 적어도 개량한 적이 있어야 한다. 대포가 아니라 다른소형 화기를 고안하거나 개량해도 좋다. 하지만 사실을 말하면 15연발 권총이나 회전식 소총,사벨 권총 따위를 고안한 사람은 별로 높은 평가를 받지 못했다. 대포를 고안하거나 제작한 사람이 어떤상황 에서도 그들보다 우위를 차지했다.

대포클럽에서 가장 박식한 연설자는 이렇게 말했다.

“얼마나 존경을 받느냐는 그 사람이 고안한 대포의 무게에 정비례하고, 포탄이 도달하는 거리의 제곱에 정비례한다!”

이것이야말로 뉴턴의 만유인력 법칙을 인간 심리에 적용한 것이었다.

대포클럽의 회원이 되기 위해서는 대포, 최소한 총을 만들어 본 경험이 있어야 한다네요. 그 중에서도 특별히 존경받는 회원이 되기 위해서는 크고 포탄을 멀리 날리는 대포를 만들어야 합니다. 존경받는 정도가 ‘대포의 무게에 정비례하고, 포탄이 도달하는 거리의 제곱에 정비례’한다고 하니까요. 쥘 베른은 이를 두고 뉴턴의 ‘만유인력의 법칙’을 인간 심리에 적용했다고 했습니다.

여기서 말한 ‘존경의 법칙’은 만유인력의 법칙을 패러디한 것이지만 실제와는 조금 다릅니다. 만유인력은 두 물체 사이 거리의 제곱에 ‘반비례’하거든요. 무슨 차이인지 자세히 알아봅시다.

비례는 서로 관련 있는 두 수가 있을 때 한쪽 수가 변하면 다른 쪽 수도 그에 따라 변하는 관계를 말합니다. 한쪽이 증가하면 다른 쪽도 증가할 경우를 ‘정비례’, 한쪽이 증가할 때 다른 쪽이 줄어드는 경우를 ‘반비례’라고 하지요. 식으로 나타내면 알기 쉽습니다.
 

만유인력 공식의 만유인력상수는 만유인력의 정확한 크기를 계산하기 위해 정해져 있는 수입니다. 존경심은 사람의 마음이라 만유인력처럼 정확한 수치를 구하기는 어려워서 비례 관계만표시했습니다. 이렇게 식으로 표현해 보면 존경심은 포탄이 멀리 날아갈수록 커지지만, 만유인력은 두 물체 사이의 거리가 멀어질수록 작아지게 되어 있습니다. 결국 ‘존경의 법칙’은 ‘만유인력의 법칙’을 완벽히 패러디했다고 볼 수는 없습니다. 그래도 사람의 심리를 이렇게 수학 공식으로 표현할 수 있다니 신기하네요.

지구와 달의 인력 중심은?

첫 번째 질문 - 포탄을 달에 쏘아 보내는 것은 가능한가?
가능합니다. 포탄을 초속 12킬로미터의 초속도로 발사하면 달에 보낼 수 있습니다. 계산 결과는 이 속도로 충분하다는 것을 보여줍니다. 포탄이 지구를 떠나면 중력은 거리의 제곱에 반비례하여 줄어듭니다. 즉 거리가 3배로 늘어나면 중력은 9분의 1로 줄어듭니다. 따라서 포탄의 무게는 급속히 줄어들어, 지구에서 달까지 거리의 52분의 47을 갔을 때 달의 인력과 지구의 인력이 균형을 이루면서 포탄의 무게는‘제로’가 될 것입니다. 포탄이 그 위치를 통과하면 이번에는 달의 인력에만 이끌려 달로 떨어질 것입니다.

대포클럽의 회원들은 케임브리지천문대에 정말로 대포를 이용해 달에 갈 수 있는지 물어 봅니다. 케임브리지천문대의 과학자들은 지구에서 달까지 거리의 52분의 47만큼 가면 지구와 달의 중력이 균형을 이뤄 포탄의 무게가 없어진다고 대답하는데요, 이 수는 과연 어떻게 나온 것일까요?
 
앞서 보여 준 만유인력의 법칙에서 알 수 있듯이 중력은 두 물체의 질량에 비례하고 두 물체 사이의 거리의 제곱에 반비례합니다. 따라서 지구와 달 사이의 인력이 어디서 균형을 이루는지 알기 위해서는 지구와 달의 질량의 비를 알아야 합니다. 지구는 달보다 81배 무거우므로 이를 이용해 계산해 봅시다.
 

지구에서 달까지 거리의 52분의 47 되는 지점에서 지구와 달의 중력이 완벽한 평형을 이루지는 않지만 거의 비슷하다는 사실을 알 수 있습니다. 소설 속에 잠깐 등장하는 수치라고 해도 과학적인 사실을 바탕으로 정확히 계산해서 쓴 쥘 베른이 대단해 보입니다.

어디를 겨냥해야 할까?

포탄이 초속 12킬로미터의 초속도를 유지한다면, 목적지에 도달할 때까지 9시간밖에 걸리지 않을 것입니다. 하지만 속력은 계속 떨어질 테니까, 계산해 보면…(중략)…따라서 달이 목표 위치에 오기 97시간 13분 20초 전에 포탄을 발사해야 합니다.
(중략)

여섯 번째 질문 - 포탄이 발사될 때 달은 정확히 어느 위치에 있어야 하는가?
달은 하루에 13도 10분 35초*씩 나아가는데, 포탄이 발사될 때 달은 그 네 배인 52도 42분 20초만큼 천정에서 떨어져 있어야 합니다. 이것은 포탄이 날아가는 동안 달이 날아가는 거리입니다.

대포클럽 회원들의 문의에 대한 과학자들의 답변이 이어집니다. 포탄이 달에 도착하는 데 걸리는 시간이 97시간 13분 20초, 즉 약 4일이 걸린다고 하네요.

이어지는 질문은 ‘그러면 어디를 겨냥해서 쏴야 할까?’입니다. 언뜻 생각하면 달을 겨냥해서 쏘면 될 것 같지만 달을 향해 쏘면 포탄이 움직이는 동안 달도 움직여서 완전히 빗나가겠죠. 그래서 4일 후 달이 있을 곳을 계산해서 그 곳을 향해 대포를 쏠 계획입니다.

과학자들의 답변에는 달이 하루에 13도 10분 35초씩 움직인다는 말이 있습니다. 달이 보름달에서 다시 보름달이 되기까지는 약 29.5일이 걸리므로 한 바퀴인 360도를 29.5로 나눠 보면 다음과 같습니다.

360도 ÷ 29.5 = 12도 12분

본문에 나온 과학자들의 답변과 다르네요? 케임브리지천문대의 과학자들이 달의 다른 공전주기를 바탕으로 계산했기 때문입니다. 29.5일은 달이 지구 주위를 공전하는 동안 지구가 태양 주위를 공전한 것까지 감안한 수치거든요. 지구가 공전한 만큼 달이 지구 주위를 추가로 더돌아야 하기 때문에 시간이 길어진 겁니다. 이것을 삭망월이라고 하지요.

달이 지구 주위를 순수하게 한 바퀴 도는 데는 약 27.3일이 걸리며, 이것을 항성월이라고 합니다. 따라서 달이 지구 주위를 도는 속도를 계산할 때는 항성월을 이용해야 합니다.

360도 ÷ 27.3 = 13도 11분

항성월로 계산하니 본문의 수치가 옳다는 것을 알 수 있습니다. 이를 이용해 포탄이 달까지 가는 데 걸리는 4일 뒤에 달이 있을 곳을 예측해 대포를 쏘면 되겠죠?

* 각도의 단위 360도는 완전한 한바퀴를 말하며 60분은 1도, 60초는 1분을 나타낸다.

어디서 쏴야 할까?

달이 *천정에 왔을 때 포탄을 발사해야 하니까, 대포가 천정을 겨누어야 하는 것은 분명합니다. 따라서 궤도는 수평면에 대해 수직이 되고, 포탄은 지구 중력에서 더 빨리 벗어날 것입니다. 하지만 달이 정해진 지점의 천정까지 올라오려면, 발사 지점의 위도가 달의 적위보다 높으면 안 됩니다. 다시 말해서 그 지점은 위도 0도와 28도 사이에 있어야 합니다. 다른 지점에서 포탄을 발사하면 달을 비스듬히 겨눌 수밖에 없을 것이고, 그렇게 되면 성공할 확률이 떨어집니다.

대포를 어디에 설치해야 하는지가 문제가 되고 있습니다. 공기의 저항을 가능한 적게 받고 지구 중력에서 빨리 벗어나려면 천정을 향해 수직으로 쏘는 것이 좋습니다. 그러기 위해서는 달이 천정에 오는 곳에 대포를 설치해야 합니다. 과학자들에 따르면 위도 0도와 28도 사이에 설치해야 달이 천정에 올 수 있다고 하는데요, 왜 그럴까요?

지구에서 보았을 때 태양이 움직이는 길, 즉 황도는 지구의 적도에서 약 23도 기울어져 있습니다. 그리고 달이 움직이는 길, 백도는 황도보다 약 5도 더 기울어져 있습니다.

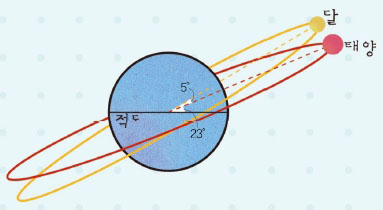
따라서 백도는 지구의 적도에서 약 28도 가량 기울어져 있습니다. 지구 위의 사람이 보았을 때 달이 수직으로 천정에 오는 것이 위도 0도에서 28도 사이에 있는 곳에서만 가능한 이유입니다.

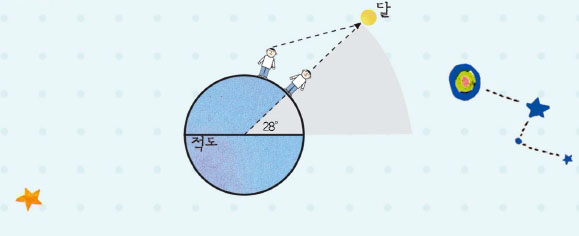
* 천정 지구에 서 있는 관측자의 머리 바로 위 방향에 있는 점.

쥘 베른은 대포를 수직으로 쏘아 올려야 한다고 했지만, 실제 로켓을 발사할 때는 동쪽으로 약간 기울인다.  지구의 자전을 이용해 연료를 절약할 수 있기 때문이다. 지구는 시속 1700km의 속도로 서쪽에서 동쪽으로 자전하기 때문에 동쪽을 향해 발사하면 자전 속도의 도움을 얻을 수 있다. 반대로 서쪽을 향해 발사한다면 자전 속도만큼 손해를 보기 때문에 효율이 떨어진다.

배율을 높여라!

앞에서 보았듯이, 반사망원경에서 확대상을 만드는 것은 접안경이다. 그리고 대물렌즈의 지름과 초점거리가 클수록 배율도 커진다. 4만 8000배의 배율을 얻기 위해서는 허셜과 로스 경의 대물렌즈보다 훨씬 큰 반사경을 만들어야 하는데, 여기에 어려움이 있었다. 그렇게 큰 거울을 만드는 것은 아주 정밀한 작업이기 때문이다.
(중략)

새로 만들 망원경의 길이는 85미터가 되어야 하고 반사경의 지름은 5미터에 이르러야 했다.

대포클럽 회원들은 사람을 태운 포탄이 무사히 달에 도착했는지 확인하기 위해 거대한 망원경을 만들려고 합니다. 아주 멀리 떨어진 곳에 있는 작은 포탄 하나를 눈으로 확인하려면 배율이 엄청나게 높은 망원경이 필요합니다. 과학자들의 계산에 따르면 배율이 4만 8000배가 되어야 한다고 하네요.

망원경의 배율은 대물렌즈의 초점거리와 대안렌즈의 초점거리에 의해 정해집니다. 대물렌즈는 물체에서 나온 상이 처음으로 통과하는 렌즈며, 대안렌즈는 우리가 들여다보는 렌즈입니다.반사망원경의 경우라면 대물렌즈 대신에 반사경이 쓰이지요.
 

배율은 대물렌즈의 초점거리가 클수록, 대안렌즈의 초점거리가 작을수록 커집니다. 오늘날 일반인이 사용하는 천체망원경에 쓰는 대안렌즈의 초점거리는 2~10mm이므로, 대안렌즈의 초점거리를 5mm라고 했을 때 4만 8000배의 배율을 얻으려면 대물렌즈의 초점거리는 240m가 되어야 합니다.

그런데 대포클럽 회원들이 만든 망원경의 길이는 85미터에 불과합니다. 아무래도 이번에는 쥘 베른이 계산을 그다지 정확하게 한 것 같지 않습니다. 어쨌든 실제로는 단순히 배율만 높다고 선명한 상을 볼 수 있는 것은 아닙니다. 망원경을 크게 만들려면 굉장히 복잡하고 어려운 기술이 필요하거든요. 쥘 베른의 상상대로 단순히 거대하기만 한 망원경을 만들어 포탄을 관측하는 것은 불가능에 가깝습니다.

Epilogue_마침내 대포는 3명의 모험가를 태운 포탄을 달을 향해 쏘아 올립니다. 4일뒤 거대한 천체망원경으로 달을 관측한 결과 포탄을 발견하지만, 계산이 약간 틀렸는지 포탄은 달에 착륙하지 못한 채 달 주위를 돌고 있습니다. 이 포탄에 탄 3명의 운명은 어떻게 될까요? 뒷이야기는 후속작인 ‘달나라탐험’에서 이어집니다.