d라이브러리

이러지도 저러지도 못하는 역설의 논리
 

드라마 ‘선덕여왕’에는 미실 새주가 비담과 불꽃튀는 머리싸움을 하는 장면이 나온다. 하늘과 소통하는 능력을 가졌다는 비담에게 미실 새주는 “네 놈은 언제 죽게 될 것 같으냐?”고 묻는다. 만약 오늘 죽는다고 하면 내일 죽일 것이고, 내일 이후라면 당장 죽이려는 심보였다. 이 때 비담은 “소인의 명운은 신국의 임금이신 폐하보다 3일이 모자라는 운명이옵니다”라고 답한다. 자신이 죽으면 3일 뒤에 왕도 죽을 것이라고 말해 자신을 죽이지 못하게 한 것이다. 이러지도 저러지도 못하는 상황을 피한 비담의 지혜가 돋보이는 장면이다.

수학에는 비담이 처한 상황과 비슷한 ‘역설’이 존재한다. 역설이란 논리적으로 모순인 결론이 나타난 경우를 뜻한다. 영국의 수학자 버트런드 러셀은 1901년 “자신을 원소로 갖지 않는 모든 집합들의 집합 A가 있을 때, A는 자기 자신을 원소로 포함 하는가”의 문제가 역설이라는 것을 처음으로 밝혔다. 만약 A가 자신을 원소로 포함하지 않는다면 집합 A의 정의에 따라 자신은 A의 원소가 돼야 한다. 반대로 자신을 A의 원소로 포함한다면 집합 A의 정의에 어긋나게 된다.

러셀은 역설을 설명하며 ‘세비야의 이발사'를 예로 들었다. 스페인 세비야의 한 이발사가 문 앞에 “스스로 면도하지 않는 모든 사람만을 면도해 주겠다”고 써 놓았다고 한다. 그럼 이 이발사의 면도는 누가 할 수 있을까? 만약 이 이발사가 스스로 면도를 한다면 스스로 면도하지 않는 사람만을 면도한다는 전제를 어긴 셈이 된다. 스스로 면도를 하지 않는다면 전제에 따라 자신이 스스로를 면도해야 하는 역설에 빠진다.

오래된 시에서도 역설을 찾아볼 수 있다. 기원전 6세기경 크레타 섬의 시인이자 철학자인 에피메니데스는 제우스신에게 ‘크레티카’라는 시를 써서 바쳤다. 제우스신은 죽었다고 말하는 크레타인을 비판하며 제우스신을 경배하는 내용의 시다. 여기에는 “모든 크레타인은 거짓말쟁이다”라는 표현이 나온다. 짧은 문장이지만 에피메니데스 자신이 크레타인이라는 점 때문에 지금까지 유명한문장이 되고 있다.

만약 에피메니데스가 거짓말쟁이가 아니라고 하자. 그럼 “모든 크레타인은 거짓말쟁이다”라는 말이 참이 되는데, 문제는 자신도 크레타인이므로 그 역시 거짓말쟁이가 된다. 에피메니데스가 거짓말쟁이가 아니라는 가정과 모순이 된다. 반대로 에피메니데스가 거짓말쟁이라고 하자. 이러면 그가 한 말 “모든 크레타인은 거짓말쟁이다”도 거짓말이므로 크레타인의 한 사람인 에피메니데스는 거짓말쟁이가 아니게 된다. 그럼 에피메니데스가 거짓말쟁이라는 가정과 모순이 된다. 참과 거짓의 두 명제에 각각 모순인 결론을 낳는 점에서 이 문장은 ‘크레타인의 역설’로 알려져 있다.

1913년 영국의 수학자 주르당은 ‘카드 역설’을 새롭게 선보였다. 그는 아무것도 적히지 않은 카드 한 장을 꺼내 앞면에 “이 카드의 뒷면에 적힌 문장은 진실”이라고 썼다. 그리고는 카드를 뒤집어 “이 카드의 다른 면에 적힌 문장은 거짓”이라고 썼다. 앞면의 문장이 참이면 뒷면의 문장은 진실이되어야 한다. 뒷면의 문장이 진실이려면 앞면의 문장이 거짓이어야 한다. 결국 앞면의 문장이 참이라는 가정과 모순을 이룬다. 앞면의 문장이 처음부터 거짓이라면, 뒷면의 문장은 거짓이 되고 그러면 다시 앞면의 문장이 참이어야 한다. 이 또한 모순이다.
 

크레타인의 역설은 역설이 아니다!

현대 논리학은 크레타인의 역설이 실제로는 역설이 아니라고 설명한다. 과거에는 “모든 크레타인은 거짓말쟁이다”의 부정형을 “모든 크레타인은 거짓말쟁이가 아니다”라고 판단한 결과 역설이라고 생각했다. 현대에서는 이 문장의 부정형이 “어떤 크레타인은 거짓말쟁이가 아니다”라고 해야 논리에 맞다는 것을 발견했다.그러면 에피메니데스가 크레타인이면서 참도 말할 수 있어 역설을 피할 수 있다.


아킬레스보다 빠른 거북?

그리스 신화의 영웅 아킬레스에게 세상에서 가장 빠른 거북이 달리기 경주를 신청했다. 아킬레스는 1초에 10m를 달릴 수 있고, 거북은 1초에 1m를 달릴 수 있다고 하니 승부는 결정난 것이나 다름이 없다. 거북은 대신 한 가지 조건을 내걸었다. 자신이 느린 만큼 아킬레스보다 10m 앞에서 출발하겠다는 것이다. 10m 정도야 금세 따라 잡을 것이라 확신한 아킬레스는 거북의 조건을 받아들였다. 과연 아킬레스는 이 경주에서 이길 수 있을까?

그리스의 철학자 제논은 거북의 승리를 장담했다. 아킬레스가 거북을 따라 잡으려고 아무리 애써도 결코 거북을 따라잡지 못한다는 것이다. 제논에 따르면 아킬레스가 10m지점에 도착했을 때, 거북은 이미 10+A 지점에 가 있다. 아킬레스가 10+A 지점에 왔을 때 거북은 조금 더 앞인 10+B 지점에 있다. 이처럼 아킬레스가 아무리 달려도 거북은 항상 조금씩 더 앞에 가 있게 된다.

그럼 상식에 따라 아킬레스가 거북을 언제 따라잡을 수 있는지 계산해 보자. 달리기를 시작한지 1초가 지나 아킬레스가 10m지점에 왔을 때, 거북은 10+1=11m에 도착한다. 1.1초 뒤라면 아킬레스는 11m, 거북은 10+1.1=11.1m에 가 있다. 조금만 시간을 더 보태면 따라잡을 수 있을 것 같다. 만약 1.11초 뒤라면 아킬레스는 11.1m, 거북은 10+1.11=11.11m에 있다. 아킬레스가 이길거라는 상식에 맞춰 계산한 것인데도 뭔가 이상하다. 이것은 무한 반복이 무한한 결과를 낳아 아킬레스가 거북을 결코 따라잡지 못한다고 생각하는 데 문제가 있다.
 

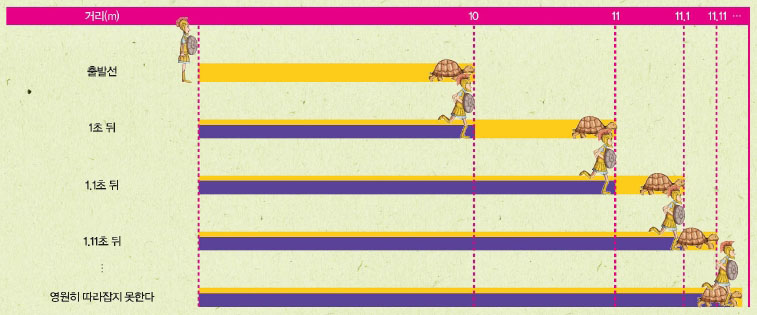
제논의 역설

기원전 5세기경 그리스의 수학자 제논은 “사물이 움직인다고 느끼는 것은 모두 환상”이라는 파르메니데스의 사상을 지지하기 위해 아킬레스의 역설 외에도 물체나 화살이 움직일 수 없다는 역설을 주장했다.