d라이브러리

여러분은 뫼비우스 띠를 보면 무엇이 떠오르나요? 무한의 상징? 재활용 심볼? 수학자들은 50년 전부터 ‘직사각형’을 생각해왔습니다(아니, 대체 왜). 가장 작은 뫼비우스 띠를 만드는 직사각형은 어떤 모양일까 하고요. 그 질문의 답이 지난 8월 드디어 풀렸습니다.

어떻게 풀었을까요? 그보다, 수학자들은 대체 왜 이런 걸 궁금해할까요?

활동지 B의 양쪽 끝에는 화살표가 있습니다. 이 화살표가 같은 방향으로 만나게 구부리면, 가운데가 뚫린 원기둥이 만들어집니다. 자, 이제 두 마리 개미를 데려와 빨간선쪽에 한 마리, 파란선쪽에 한 마리 올려둡니다. 두 개미는 평생 동안 전진해도 서로 만날 수 없습니다. 두 공간은 분리돼 있으니까요.

두 개미를 만나게 해주는 방법은 쉽습니다. 종이 끝의 화살표가 서로 다른 방향으로 만나게 하는 거죠(초록선을 따라 접으면 접착면끼리 쉽게 만날 수 있습니다). 그럼 빨간선과 파란선이 자연스럽게 이어지면서 서로 다른 공간에 있던 개미들이 마주치게 됩니다. 이처럼 선이 하나로 이어지고, 면의 안과 밖의 구별이 없는 신기한 곡면을 뫼비우스 띠라고 부릅니다(활동지 B로 만든 뫼비우스 띠는 뫼비우스 띠 B라고 합시다).

뫼비우스 띠는 1858년 독일의 수학자 아우구스트 페르디난트 뫼비우스가 발견해 지금의 이름이 붙었습니다. 요한 베네딕트도 독자적으로 발견했으나, 독일의 수학자 뫼비우스가 더 많이 언급해 뫼비우스 띠라고 불립니다.

위상수학의 발전을 이끈 뫼비우스 띠

뫼비우스 띠는 위상수학 분야에서 매우 흥미롭고 중요한 곡면입니다. 그 이유는 위상수학의 본질에 있습니다. 위상수학은 눈에 보이는 대로 도형을 분류하는 것이 아니라, 도형의 본질에 따라 분류하는 학문입니다. 도형이 말랑한 찰흙이라고 가정했을 때 조물조물 만져서 같은 형태로 만들 수 있다면, 같은 도형이라고 보는 거죠. 위상수학 관점에서 도넛과 머그컵은 같은 위상인 도형입니다. 도넛과 머그컵 모두 잘 다듬으면 구멍이 하나인 원환면으로 만들 수 있기 때문이죠.

위상수학은 비교적 최근에 생긴 현대 수학입니다. 연구 초기였던 19세기 말에는 모든 곡면을 분류할 수 있는 기준을 만드는 것이 중요한 과제였습니다. 초창기 수학자들은 ‘오일러 종수’라는 공식을 통해 꼭짓점, 모서리, 면의 개수를 계산한 값으로 곡면을 분류했습니다. 하지만 오일러 종수만으로는 모든 곡면을 완벽하게 분류할 수 없었습니다. 그러다 뫼비우스 띠라는 새로운 아이디어가 등장했습니다. 뫼비우스 띠의 특징인 방향성으로 곡면을 분류하는 아이디어였죠. 실제로 오일러 종수와 방향성을 이용하면 모든 곡면을 구분할 수 있어 뫼비우스 띠는 위상수학에서 중요한 의미를 갖습니다.

뫼비우스 띠를 만들 수 있는 가장 작은 직사각형

뫼비우스 띠는 길쭉한 직사각형을 한 번 꼬아서 만들 수 있습니다. 하지만 남다른 수학자들은 이런 질문을 던집니다. ‘정사각형으로 뫼비우스 띠를 만들 수는 없을까?’ ‘만들 수 없다면, 높이와 너비의 비율이 얼마인 직사각형까지 뫼비우스 띠를 만들 수 있을까?’ 미국의 수학자 찰스 시드니 위버와 벤저민 리글러 핼펀은 1977년 이런 질문을 처음으로 제기했습니다. 그 후 수많은 수학자들이 답을 찾아 헤맸죠. 바로 그 해답이 지난 8월 밝혀졌습니다. 거의 50년 만입니다.

이번에는 뫼비우스 띠 A를 보면서 읽어주세요

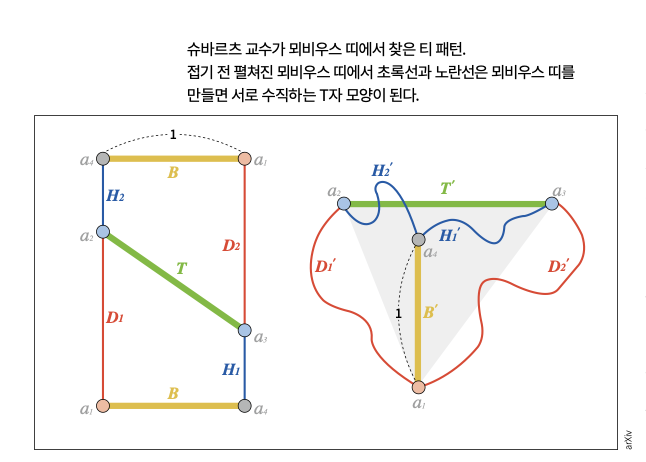
리차드 이반 슈바르츠 미국 브라운대 수학과 교수는 4년을 고민한 끝에 ‘티 패턴’이라는 보조 정리로 질문의 답을 증명하는 데 성공했습니다. ^{doi: 10.48550/arxiv.2308.12641} 티 패턴을 이해하기 위해 먼저 높이와 너비가 1 대 루트3비율인 활동지 A로 뫼비우스 띠 A를 만들어봅시다(루트3은 무한 소수이기 때문에 조금의 오차가 있을 수 있습니다). 아까 만든 뫼비우스 띠 B보다는 만들기 어려울 겁니다. 양 끝이 쉽게 만나지 않으니까요. 하지만 활동지의 점선을 따라 접고, 무한한 상상력을 보태면 불가능하지 않습니다. 점선을 따라 접으면 두 화살표가 반대로 만나게 됩니다. ‘이건 정삼각형 아닌가?’ 생각할 수 있지만 ‘밴드의 양끝의 방향이 다르게 만난다’라는 조건을 만족했으니 뫼비우스 띠가 맞습니다. 정삼각형 모양의 뫼비우스 띠죠.

슈바르츠 교수는 뫼비우스 띠에는 반드시 ‘티 패턴’이 있다는 것을 확인했습니다. 티 패턴을 이해하기 위해 77쪽 아래그림을 살펴봅시다. 직사각형의 양 변을 연결하는 두 선 ‘T’와 ‘B’가 공간 속 뫼비우스 띠 상태에서 수직하게 될 때 이 두 선을 의미합니다. 두 직선이 알파벳 ‘T’ 모양으로 교차돼 붙인 이름입니다. 아래 그림에서 노란선과 초록선이 티 패턴입니다.

활동지에서도 티 패턴을 찾아볼까요? 뫼비우스 띠 A, B에서 노란선과 초록선을 연장하면 두 선이 수직한 것을 확인할 수 있습니다. 이렇게 수직한 모양을 기준으로 만든 삼각형이 바로 아래 오른쪽 그림이죠. 공간에서 이해해보면 활동지에 있는 점 a₁, a₂, a₃를 연결한 삼각형을 말합니다. 슈바르츠 교수는 뫼비우스 띠를 만들 수 있는 가장 작은 직사각형의 비율을 이 삼각형의 성질을 이용해 최적화 문제로 바꿔 풀었습니다.

수학자들은 왜

최수영 아주대 수학과 교수에게 한 시간 가량 연구에 대한 설명을 듣고 나니 머릿속이 아득해졌습니다. 오랜만에 사고력과 공간지각능력을 풀가동하는 시간이었거든요. 겨우 정신을 차리니 이런 생각이 들었습니다(사실 처음부터 든 생각일지도 모릅니다). ‘수학자들은 왜 이런걸 궁금해하지?’

최 교수는 웃으며 “불가능성에 대해 이야기하는 것은 수학의 기본적인 질문”이라고 답했습니다. 그는 과학과 비교해 설명했습니다.

“화성에 100년 뒤에 사람이 살 수 있을까? 암을 정복할 수 있을까? 이 질문에 대한 정답은 시간이 흐르면서 변합니다. 지금은 불가능해도 기술이 발전하면 언젠가 가능해질 수 있으니까요. 이건 불가능과 가능의 문제죠. 그런데 수학은 영원히 불가능한 ‘부존재’와 특정 조건 하에서 언제나 가능한 ‘유일성’에 대한 이야기를 하는 학문입니다.” 뫼비우스 띠를 비율이 1: 루트3 보다더 작은 직사각형으로 만들 수 있느냐 없느냐는 부존재를 탐구하는 수학자들에겐 매우 흥미로운 문제라는 겁니다.

“이번 증명이 수학계에 도움이 될 수 있을까요?” 기자의 질문에 최 교수의 답은 간결했습니다. “없을 겁니다. 그래도 수학자들은 이런 걸 궁금해 해요. 수학에서 할 수 없다는 걸 아는 것과 모르는 것은 엄청난 차이거든요.”