파피루스는 나일강 유역에 자라는 식물로, 줄기 껍질을 벗겨내고 가공하면 그 위에 기록을 남길 수 있다. 고대 이집트의 파피루스 중에서 특히 주목을 받는 책은 기원전 1650년 경 저술된 것으로 추정되는 ‘린드 파피루스’다. 이 책의 제목은 1858년 이집트에서 파피루스를 구입해 세상에 알리는 데 기여한 스코틀랜드의 골동품상 린드(Alexander Henry Rhind)의 이름을 딴 것이다. 파피루스에 필사본을 남겼던 서기(書記) 아메스의 이름을 따서 ‘아메스의 파피루스’라고도 한다. 폭 33cm, 길이 약 5m인 이 책은 현재 대영박물관에 전시돼 있다.
고대 이집트인들이 사랑한 ‘공평한’ 단위분수
고대 이집트인들은 분자가 1인 단위분수를 유독 선호했다. 린드 파피루스에도 n이 홀수이면서 5≦n≦101인 형태의 분수를 여러 단위분수의 합으로 나타낸 문제가 실려 있다.
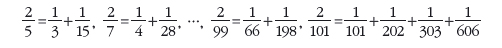

다시 말해, 네 명은 2/5조각을 1개씩 갖고 한 명은 1/5조각을 2개 갖는다. 공평하게 나눈 것처럼 보이지만 사실은 그렇지 않다. 최종적으로 갖게 되는 ‘양’은 2/5로 동일하지만, 2/5조각 1개와 1/5조각 2개의 ‘질’은 같지 않기 때문이다.
그런데 이를 단위분수의 합으로 나타내면 이런 불공평함이 사라진다. 2/5를 단위분수의 합으로 나타내면 2/5=1/3+1/15이다. 먼저 사과 2개를 각각 3등분해 크기가 1/3인 조각 6개로 만든 후 한 조각씩 나눠 갖는다. 크기가 1/3인 남은 조각 하나를 5등분하고 1/15인 조각들을 각각 갖는다. 그러면 5명 모두 공평하게 1/3조각 하나와 1/15조각 하나를 갖게 된다.



그런데 이를 단위분수의 합으로 나타내면 이런 불공평함이 사라진다. 2/5를 단위분수의 합으로 나타내면 2/5=1/3+1/15이다. 먼저 사과 2개를 각각 3등분해 크기가 1/3인 조각 6개로 만든 후 한 조각씩 나눠 갖는다. 크기가 1/3인 남은 조각 하나를 5등분하고 1/15인 조각들을 각각 갖는다. 그러면 5명 모두 공평하게 1/3조각 하나와 1/15조각 하나를 갖게 된다.