르네상스 시대의 화가 자코포 데 바르바리는 1495년, ‘파치올리의 초상’이라는 그림을 그렸다. 이 작품의 주인공인 파치올리(1445~1514)는 르네상스 시대 이탈리아의 수학자이자 수도사였다.
수학자를 주인공으로 한 그림답게 수학과 관련된 다양한 소재가 담겨 있다. 그림 오른쪽 아래에는 정다면체인 ‘정십이면체’가 놓여 있고, 파치올리는 오른손으로 정십이면체의 면 모양인 오각형을 컴퍼스로 그리고 있다. 파치올리가 왼손으로 가리키고 있는 책은 정다면체가 설명돼 있는 유클리드의 ‘원론’ 13권이며, 그림 왼쪽에는 준정다면체의 일종인 ‘부풀린 육팔면체’가 매달려 있다.
레오나르도 다빈치가 그려준 부풀린 육팔면체
정다면체는 서로 합동인 정다각형으로 만든 입체다. 각 꼭짓점에 모인 면 개수도 같다. 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체 등 5가지 종류가 있다. 반면, 정다면체의 조건을 일부만 만족하는 입체는 ‘준정다면체’라고 부른다. 준정다면체는 두 종류 이상의 정다각형으로 만들어지며, 각 꼭짓점에는 같은 종류의 정다각형이 같은 개수만큼 모여 있다.
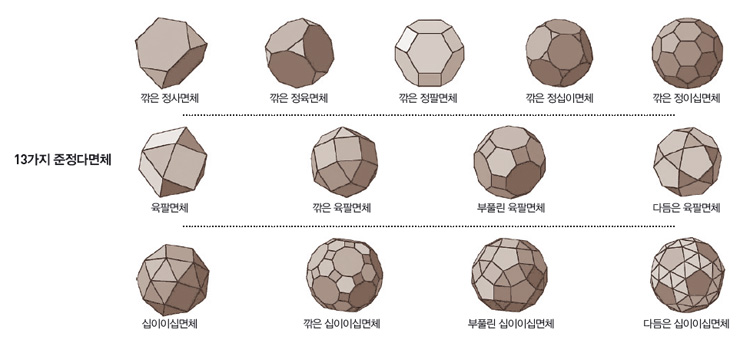
준정다면체를 처음 연구한 사람은 아르키메데스다. 그러나 그가 남겼던 기록은 현재는 거의 분실되고 없다. 이보다 활발하게 연구가 이뤄진 것은 르네상스 시대, 바로 파치올리에 이르러서다. 파치올리는 1509년 출간한 ‘신성 비례’에서 깎은 정다면체 5가지와, 육팔면체, 부풀린 육팔면체, 십이이십면체 등 8가지 준정다면체를 소개했다.
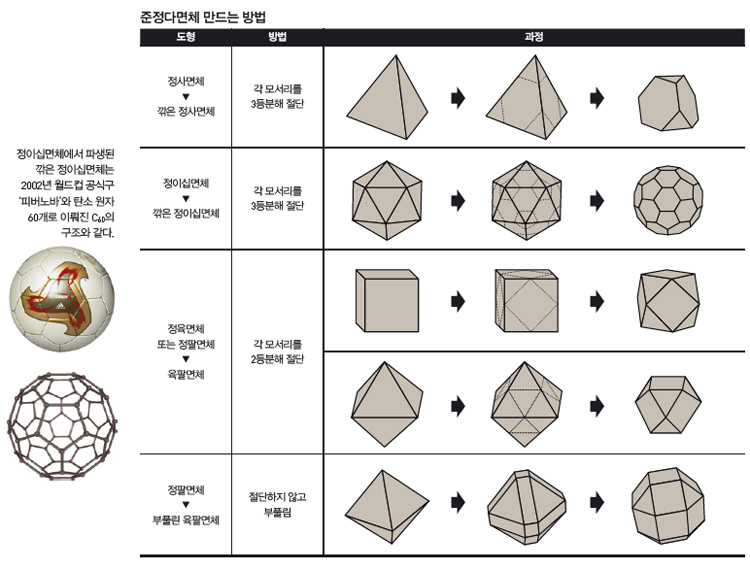
깎은 정다면체는 정다면체의 한 꼭짓점을 기준으로 그 점에 연결된 모든 모서리의 3등분점을 이어 절단해 버린 입체다. 이 규칙에 따라 정사면체의 네 꼭짓점을 절단하면(134쪽 그림 참고), 네 개의 새로운 정삼각형 단면이 생기고, 원래 삼각형이었던 정사면체의 각 면은 정육각형으로 바뀐다. 따라서 깎은 정사면체는 합동인 정삼각형 4개와 합동인 정육각형 4개로 이뤄진다. 모든 꼭짓점에는 정삼각형 1개와 정육각형 2개가 모이게 된다.
같은 방법으로 만든 ‘깎은 정이십면체’는 모든 꼭짓점에 정오각형 1개와 정육각형 2개가 모여 있다. 1970년 멕시코 월드컵에 등장한 공식구 ‘델스타’가 깎은 정이십면체 형태로 만들어진 축구공의 시초다. 월드컵 공식구로는 2002년 ‘피버노바’까지 이어졌다.
깎은 정이십면체는 화학 분자에서도 찾아볼 수 있다. 1985년, 탄소 원자 60개로 이뤄진 C60이 실험실에서 합성됐다. 60개 꼭짓점에 탄소 원자가 한 개씩 위치하는 구조다. 축구공과 같은 깎은 정이십면체라고 해서 별칭이 축구공(bucky ball)이다. 안정적인 구조 덕분에 고온 고압을 견딜 수 있고 방사능에 대한 저항력도 커서, 나노 기술 등 여러 분야에 이용될 가능성이 높다.

육팔면체는 정육면체로 만들 수도 있고 정팔면체로 만들 수도 있어서 이런 명칭이 붙었다. 깎은 정다면체를 만들 때 각 모서리를 3등분 하는 것과 달리, 육팔면체를 만들 때는 각 모서리의 중점을 이어 절단한다. 8개의 꼭짓점은 정삼각형이 되고 정사각형이었던 면 6개는 보다 작은 정사각형이 된다. 따라서 육팔면체는 면의 개수가 14개다. 정팔면체도 같은 방법으로 절단하면 동일한 육팔면체로 만들 수 있다.
정육면체나 정팔면체를 위의 그림과 같이 부풀리면 ‘파치올리의 초상’에 그려져 있던 ‘부풀린 육팔면체’를 만들 수 있다. 부풀리는 과정을 거치면서 정팔면체의 꼭짓점 6개는 정사각형으로 바뀌고, 12개의 모서리 역시 정사각형으로 바뀐다. 정팔면체를 이루던 정삼각형 8개는 그대로 남아 있다. 따라서 부풀린 육팔면체의 면의 개수는 총 26개가 된다. 신성 비례에 실려 있는 부풀린 육팔면체는 당시 파치올리와 친분이 있던 레오나르도 다빈치가 그렸다고 한다.
72의 법칙을 만든 ‘회계학의 아버지’
파치올리는 기하학 연구뿐만 아니라 산술 연구로도 유명하다. 그는 또 다른 저서 ‘산술집성’을 통해 일반인도 쉽게 쓸 수 있는 복리 계산 공식인 ‘72의 법칙’을 제안했다.
복리란 원금에 이자를 붙이고, 그 둘을 합한 금액에 이자를 또 붙이는 방식이다. 저축하는 사람에겐 복을 주는 복리(福利)고, 빚을 못 갚는 사람에겐 고통을 주는 폭리(暴利)가 될 수 있다. 1625년 미국 원주민은 백인 이주자에게 단돈 24달러에 맨하튼을 팔았지만, 만약 그 24달러를 연 6% 복리로 지금까지 예금해 뒀다면 158조원이라는 어마어마한 금액이 된다. 현재 맨하튼 땅값에 버금가는 돈이다. 이런 복리의 폭발력을 깨달은 아인슈타인은 “우주에서 가장 강력한 힘은 복리”라고 말했다. 전설적 펀드매니저 피터 린치는 “복리의 힘을 믿어라”는 투자 금언을 남기기도 했다.
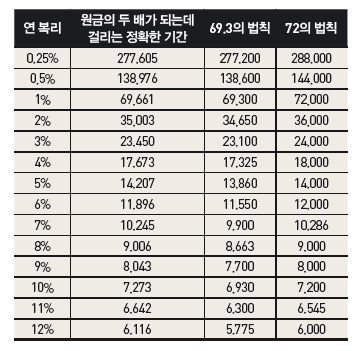
하지만 우리가 죽기 전에 복리의 힘을 느낄 기회가 과연 올까? 내가 저축한 원금이 2배가 되려면 100년이상 걸리는 것은 아닐까. 파치올리가 제안한 ‘72의 법칙’에 따르면 72를 복리금리로 나눈 기간만큼 예금해두면 된다. 예를 들어, 연복리가 4%일 때 원금이 2배가 되려면 72를 4로 나눈 18년 동안 예금해두면 된다는 뜻이다. 오차는 있지만, 비교적 정확도가 높다.
이 공식이 어떻게 나오게 됐는지 계산 과정을 살펴보자. 원금이 x원이고 연복리가 r일 때 원금의 두 배가 되는 기간을 n년이라고 하면 2x=x(1+r)n이다. x는 0이 아니므로 양변을 x로 나누면 2=(1+r)n이고, 여기에 자연로그를 취하면 ln2=ln(1+r)n=n ln(1+r)이다.
따라서
n의 근사값을 구하기 위해 분자와 분모를 살펴보자. 먼저 분자에 있는 ln2의 값은 대략 0.693이다. 분모에 있는 y=ln(1+r)은 r=0일 때 접선의 방정식이 y=r이므로 ln(1+r)≒r로 대입할 수 있다. 그런데 다음 표에서 볼 수 있듯이, 금리 r이 커지면 ln(1+r)과 r의 오차가 커지며, 0.693보다 0.72를 적용한 계산의 오차가 더 작아진다.
이렇게 r의 근사식
72는 약수가 많은 수이기 때문에 계산이 훨씬 간편하다. 일반인도 쉽게 쓸 수 있어 실용적이다. 무엇보다 오차가 작다.
파치올리는 산술집성을 통해 72의 법칙뿐만 아니라 복잡한 상거래를 한 눈에 파악하게 해주는 ‘복식부기’를 처음으로 제안하기도 했다. 당시 무역의 중심지 베네치아에서 활발하게 활동해 ‘회계학의 아버지’라는 이름도 얻었다. 르네상스 시대에 기하학과 회계학 분야에 큰 획을 그은 수학자이자 수도사였던 파치올리는 진정한 르네상스적 인간이었다.