영재성 포트폴리오는 가능한 한 독창적인 주제를 택하는 게 유리하다. 여기서 독창적이라는 것은 다른 지원자와는 차별화한 참신한 시각을 의미한다. 이번 호에 소개하는 기하 포트폴리오에서는 독창적으로 접근하는 방법을 살펴보자.
※ 이 코너에서는 실제 영재고, 과학고 합격생들의 포트폴리오 분석을 통해서 중등 영재들의 수학, 과학 탐구활동을 돕고 포트폴리오를 더욱 충실하게 만들 다양한 방법을 제시합니다.
창의적 사고는 스스로 문제를 발견하는 데에 중점을 둔다. 따라서 포트폴리오에서도 어떤 주제를 탐구하게 된 동기가 중요하다. 실제로 해석기하에 대한 탐구활동을 펼쳐 좋은 평가를 받은 사례가 있다. 이 사례를 살펴보며 창의적인 포트폴리오 작성법을 알아보자.
해석기하에 대한 탐구 사례
다음은 해석기하에 대한 포트폴리오를 작성하며 정리한 개요다.
개요
1. 탐구 동기
2. 본론
(1) 해석기하의 정의와 기본 지식
(2) 해석기하를 이용해 기하 정리 증명하기
3. 결론, 더 탐구해보고 싶은 것들과 느낀 점
이 개요는 해석기하학을 배운 학생이 이를 주요 기하 문제에 적용해 일일이 증명을 시도한 내용을 포트폴리오로 작성하기 위한 개요다. 몸소 체험한 해석기하의 편리성을 설명하면서, 한편으로는 기하 문제를 해석기하로 접근할 때 주의할 점을 스스로 깨달아가는 과정을 보여준다. 간단하면서도 포트폴리오가 갖춰야 할 중요 항목을 모두 구비한 점에 주목할 만하다. 특히 결론 부분에서 이 개요처럼 ‘탐구하면서 느낀 점, 더 탐구해보고 싶은 것’을 빠뜨리지 않도록 주의해야 한다.
영재고에 도전하는 학생이라면 해석기하에 대한 대략적인 지식을 갖고 있는 경우가 많을 것이다. 그러나 이 학생처럼 어려운 기하 문제들을 해석기하를 사용해 증명해보려고 시도하는 학생은 드물다. 참고서에 나타나는 아폴로니우스의 정리(파푸스 중선 정리)를 배우고 이를 기억하는 것이 전부이다. 이런 점에서 이 포트폴리오는 창의적인 시도가 눈에 띈다.
1. 탐구 동기
한번은 문제를 풀다가 파푸스의 중선정리를 좌표를 이용해 푸는 방법을 보게 됐다. 나중에 조사해보니 그 방법은 데카르트가 발견한 해석기하학이라는 분야에 속해 있었다는 것을 알게 됐다. 좌표를 통한 기하 문제의 해결은 나의 눈길을 끌었다.
나는 수학문제를 풀 때 일정한 양의 정보가 주어지고, 그 정보들이 어느 정도 주어져 있을 때 그것들을 조합해 새로운 결과를 도출해낼 수 있다고 생각한다. 그리고 그 주어진 정보들을 끼워맞출 수 있는 능력이 수학문제를 잘 풀 수 있느냐 못 푸느냐를 결정한다고 생각한다. 기하문제를 풀 때의 어려움 또한 주어진 조건을 어떻게 잘 끼워 맞춰서 결과를 도출하느냐 하는 것이었다. 그러나 해석기하학은 주어진 조건들을 어떻게 이용할까 고민하지 않고도, 조건들을 좌표 값에 집어넣는 과정만 거치면 된다. 새롭게 알게 된 이 방법이 신비로웠다. 다른 여러 기하 정리들도 조건을 찾은 후 그 조건을 좌표 값에 넣는 방식을 통해 직접 증명해보고 싶었다.
2. 본론
(1) 해석기하의 정의와 기본 지식
① 좌표평면 위 두 점 사이의 거리
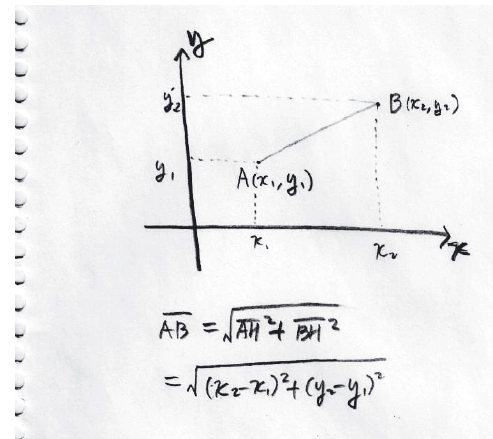
② 선분의 내분점과 외분점

③ 삼각형의 무게심의 위치
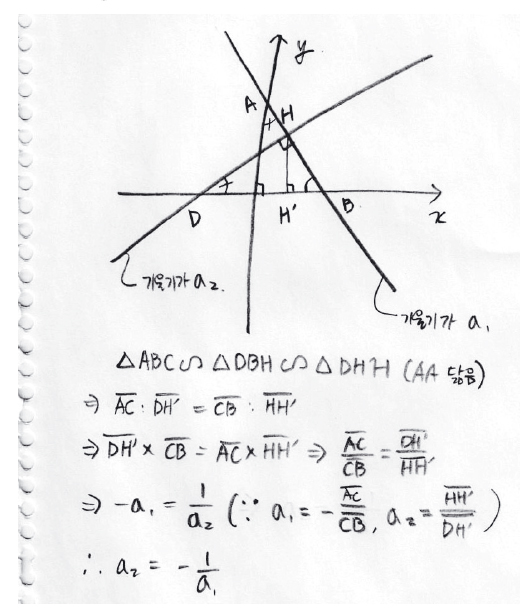
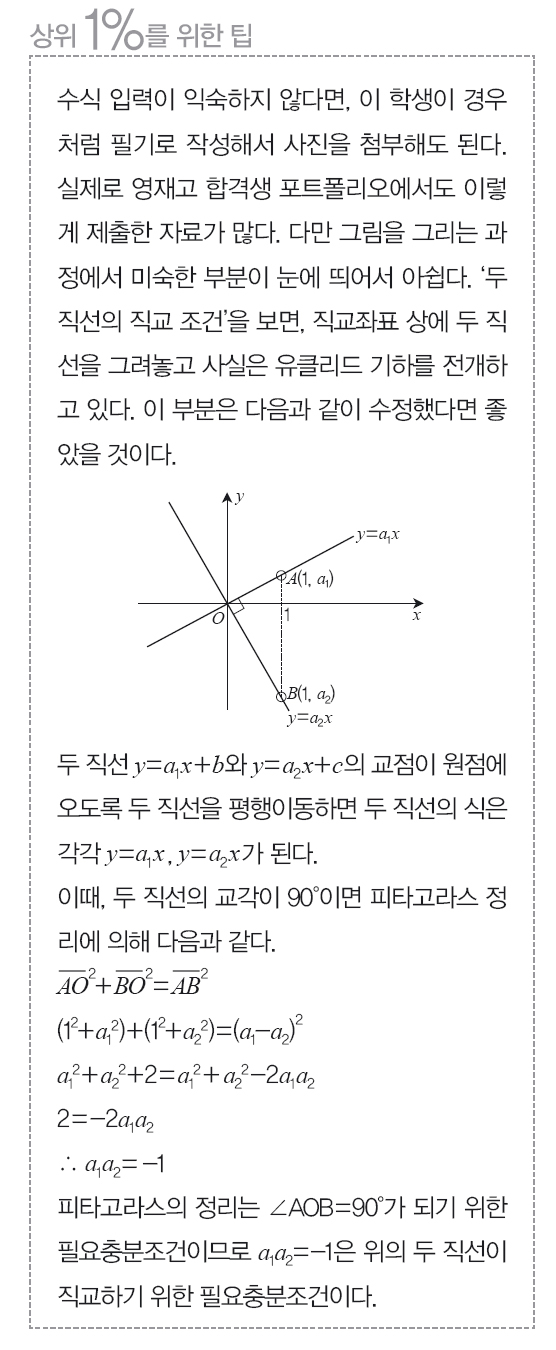
④ 기울기가 각각 인 두 직선의 직교 조건
⑤ 원의 방정식
본론의 1파트에서는 고등학교 과정에서 해석기하를 사용하는 전형적인 경우를 정리했다.
(2) 해석기하를 이용해 기하 정리 증명하기
① 스튜어트의 정리
② 메넬라오스의 정리

③ 톨레미의 정리

앞서 본론의 1파트에서는 고등학교 수준의 해석기하를 두루 공부하고 이해했다는 것을 보여줬다. 2파트에서는 기하학의 몇몇 중요한 정리들에 대해 해석기하적으로 증명을 시도했다. 스튜어트의 정리 외에도 메넬라오스의 정리나 톨레미의 정리를 해석기하적으로 증명한 것은 매우 이색적인 내용이다. 이 정리들은 그렇게 난해하거나 복잡하지 않다. 오히려 해석기하적으로 접근하는 것이 훨씬 더 복잡하다. 그러나 해석기하의 아이디어에 영감을 받은 학생이 기존의 기하 문제에 해석기하적 방법을 적용하려 했던 독창적인 시도가 심사관들에게 감동을 준 것으로 보인다.
중학교 과정에 포함되면서도 증명이 어려워 참고서에서 그 증명을 소개하지 않는 문제들에도 해석기하를 적용해봤다면 이 포트폴리오는 더욱 빛났을 것이다. 필자도 학생들에게 가르쳐야 하는 헤론의 공식에 대해 그 증명을 어떻게 해줘야 할지 고민한 적이 있다. 헤론의 아이디어는 대단히 절묘하고 난해해 학생들에게 소개하는 일이 만만치 않다. 고민 끝에 해석기하로 접근했더니 뜻밖에 손쉽게 해결돼 학생들에게 즐거운 마음으로 소개할 수 있었다.
3. 결론
… 또 해석기하학의 반대과정으로서 식의 문제를 기하문제로 바꿔 기하 개념을 이용해 식의 문제를 푸는 방식이 있다고 들었는데 이 부분도 한번 탐구해보고 싶었다.
데카르트는 벽에 달라붙어 있는 파리를 보고 파리의 위치를 어떻게 표현할까 하다가 좌표에 대한 개념을 만들어냈다고 한다. 이번 탐구를 통해 나는 일반적인 풀이를 제시해주는 좌표를 발견해낸 데카르트가 정말 대단하다고 생각했고, 내가 커서 과학자가 된다면 나도 좌표 같은 수학의 새로운 도구를 만들어 보고 싶다. …
이 학생의 포트폴리오에서 가장 돋보이는 부분은 결론 부분이다. 대체로 포트폴리오의 마지막 부분에 느낀 점과 더 연구하고 싶은 과제를 넣지만 대체로 형식적인 내용이 많다. 그에 비해 이 학생의 글은 심층적이다. 또 해석기하를 사용하기 위해 도형을 좌표평면 위에 배치할 때는 일반성을 유지하도록 유의해야 한다는 점을 분명히 깨닫고 강조하고 있다. 그러면서도 일반성을 잃지 않는 범위 내에서는 대칭성 등을 이용할 수 있도록 요령 있는 배치가 필요하다는 생각을 제시한다. 도형을 어떻게 배치하느냐에 따라 계산이 엄청나게 복잡해지거나 간단해질 수 있기 때문이다.
해석기하학의 반대과정으로서 식의 문제를 기하 문제로 바꿔(대수 문제를 기하 문제로 변형) 기하 개념을 이용해 풀어보고 싶다는 글에서 이 학생이 얼마나 심층적으로 공부했는지를 잘 알 수 있다. 수학 공부를 오래 해야 이런 방식을 어느 정도 이해할 수 있기 때문이다. 또 ‘좌표 같은 수학의 새로운 도구를 만들어 보고 싶다’는 마지막 말 또한 높이 평가할 만하다. 벡터 공간을 고안한 물리학자의 아이디어도 이러한 탐구활동에서 출발한 게 아닐까.
※ 이 코너에서는 실제 영재고, 과학고 합격생들의 포트폴리오 분석을 통해서 중등 영재들의 수학, 과학 탐구활동을 돕고 포트폴리오를 더욱 충실하게 만들 다양한 방법을 제시합니다.
창의적 사고는 스스로 문제를 발견하는 데에 중점을 둔다. 따라서 포트폴리오에서도 어떤 주제를 탐구하게 된 동기가 중요하다. 실제로 해석기하에 대한 탐구활동을 펼쳐 좋은 평가를 받은 사례가 있다. 이 사례를 살펴보며 창의적인 포트폴리오 작성법을 알아보자.
해석기하에 대한 탐구 사례
다음은 해석기하에 대한 포트폴리오를 작성하며 정리한 개요다.
개요
1. 탐구 동기
2. 본론
(1) 해석기하의 정의와 기본 지식
(2) 해석기하를 이용해 기하 정리 증명하기
3. 결론, 더 탐구해보고 싶은 것들과 느낀 점
이 개요는 해석기하학을 배운 학생이 이를 주요 기하 문제에 적용해 일일이 증명을 시도한 내용을 포트폴리오로 작성하기 위한 개요다. 몸소 체험한 해석기하의 편리성을 설명하면서, 한편으로는 기하 문제를 해석기하로 접근할 때 주의할 점을 스스로 깨달아가는 과정을 보여준다. 간단하면서도 포트폴리오가 갖춰야 할 중요 항목을 모두 구비한 점에 주목할 만하다. 특히 결론 부분에서 이 개요처럼 ‘탐구하면서 느낀 점, 더 탐구해보고 싶은 것’을 빠뜨리지 않도록 주의해야 한다.
영재고에 도전하는 학생이라면 해석기하에 대한 대략적인 지식을 갖고 있는 경우가 많을 것이다. 그러나 이 학생처럼 어려운 기하 문제들을 해석기하를 사용해 증명해보려고 시도하는 학생은 드물다. 참고서에 나타나는 아폴로니우스의 정리(파푸스 중선 정리)를 배우고 이를 기억하는 것이 전부이다. 이런 점에서 이 포트폴리오는 창의적인 시도가 눈에 띈다.
1. 탐구 동기
한번은 문제를 풀다가 파푸스의 중선정리를 좌표를 이용해 푸는 방법을 보게 됐다. 나중에 조사해보니 그 방법은 데카르트가 발견한 해석기하학이라는 분야에 속해 있었다는 것을 알게 됐다. 좌표를 통한 기하 문제의 해결은 나의 눈길을 끌었다.
나는 수학문제를 풀 때 일정한 양의 정보가 주어지고, 그 정보들이 어느 정도 주어져 있을 때 그것들을 조합해 새로운 결과를 도출해낼 수 있다고 생각한다. 그리고 그 주어진 정보들을 끼워맞출 수 있는 능력이 수학문제를 잘 풀 수 있느냐 못 푸느냐를 결정한다고 생각한다. 기하문제를 풀 때의 어려움 또한 주어진 조건을 어떻게 잘 끼워 맞춰서 결과를 도출하느냐 하는 것이었다. 그러나 해석기하학은 주어진 조건들을 어떻게 이용할까 고민하지 않고도, 조건들을 좌표 값에 집어넣는 과정만 거치면 된다. 새롭게 알게 된 이 방법이 신비로웠다. 다른 여러 기하 정리들도 조건을 찾은 후 그 조건을 좌표 값에 넣는 방식을 통해 직접 증명해보고 싶었다.
2. 본론
(1) 해석기하의 정의와 기본 지식
① 좌표평면 위 두 점 사이의 거리

② 선분의 내분점과 외분점

③ 삼각형의 무게심의 위치

④ 기울기가 각각 인 두 직선의 직교 조건
⑤ 원의 방정식
본론의 1파트에서는 고등학교 과정에서 해석기하를 사용하는 전형적인 경우를 정리했다.
(2) 해석기하를 이용해 기하 정리 증명하기
① 스튜어트의 정리
② 메넬라오스의 정리

③ 톨레미의 정리

앞서 본론의 1파트에서는 고등학교 수준의 해석기하를 두루 공부하고 이해했다는 것을 보여줬다. 2파트에서는 기하학의 몇몇 중요한 정리들에 대해 해석기하적으로 증명을 시도했다. 스튜어트의 정리 외에도 메넬라오스의 정리나 톨레미의 정리를 해석기하적으로 증명한 것은 매우 이색적인 내용이다. 이 정리들은 그렇게 난해하거나 복잡하지 않다. 오히려 해석기하적으로 접근하는 것이 훨씬 더 복잡하다. 그러나 해석기하의 아이디어에 영감을 받은 학생이 기존의 기하 문제에 해석기하적 방법을 적용하려 했던 독창적인 시도가 심사관들에게 감동을 준 것으로 보인다.
중학교 과정에 포함되면서도 증명이 어려워 참고서에서 그 증명을 소개하지 않는 문제들에도 해석기하를 적용해봤다면 이 포트폴리오는 더욱 빛났을 것이다. 필자도 학생들에게 가르쳐야 하는 헤론의 공식에 대해 그 증명을 어떻게 해줘야 할지 고민한 적이 있다. 헤론의 아이디어는 대단히 절묘하고 난해해 학생들에게 소개하는 일이 만만치 않다. 고민 끝에 해석기하로 접근했더니 뜻밖에 손쉽게 해결돼 학생들에게 즐거운 마음으로 소개할 수 있었다.
3. 결론
… 또 해석기하학의 반대과정으로서 식의 문제를 기하문제로 바꿔 기하 개념을 이용해 식의 문제를 푸는 방식이 있다고 들었는데 이 부분도 한번 탐구해보고 싶었다.
데카르트는 벽에 달라붙어 있는 파리를 보고 파리의 위치를 어떻게 표현할까 하다가 좌표에 대한 개념을 만들어냈다고 한다. 이번 탐구를 통해 나는 일반적인 풀이를 제시해주는 좌표를 발견해낸 데카르트가 정말 대단하다고 생각했고, 내가 커서 과학자가 된다면 나도 좌표 같은 수학의 새로운 도구를 만들어 보고 싶다. …
이 학생의 포트폴리오에서 가장 돋보이는 부분은 결론 부분이다. 대체로 포트폴리오의 마지막 부분에 느낀 점과 더 연구하고 싶은 과제를 넣지만 대체로 형식적인 내용이 많다. 그에 비해 이 학생의 글은 심층적이다. 또 해석기하를 사용하기 위해 도형을 좌표평면 위에 배치할 때는 일반성을 유지하도록 유의해야 한다는 점을 분명히 깨닫고 강조하고 있다. 그러면서도 일반성을 잃지 않는 범위 내에서는 대칭성 등을 이용할 수 있도록 요령 있는 배치가 필요하다는 생각을 제시한다. 도형을 어떻게 배치하느냐에 따라 계산이 엄청나게 복잡해지거나 간단해질 수 있기 때문이다.
해석기하학의 반대과정으로서 식의 문제를 기하 문제로 바꿔(대수 문제를 기하 문제로 변형) 기하 개념을 이용해 풀어보고 싶다는 글에서 이 학생이 얼마나 심층적으로 공부했는지를 잘 알 수 있다. 수학 공부를 오래 해야 이런 방식을 어느 정도 이해할 수 있기 때문이다. 또 ‘좌표 같은 수학의 새로운 도구를 만들어 보고 싶다’는 마지막 말 또한 높이 평가할 만하다. 벡터 공간을 고안한 물리학자의 아이디어도 이러한 탐구활동에서 출발한 게 아닐까.