구독상품안내
오른나사의 법칙오른나사를 전류의 방향으로 진행시키기 위해서 돌려야 하는 방향으로 자기장이 나타난다. 오른 손으로 엄지를 세워, 그 방향이 전류의 방향이면 나머지 네 손가락이 감는 방향은 자기장의 방향이다.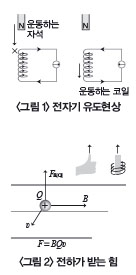
상대운동에 의한 전자기 유도현상
<;그림 1>;과 같이 막대자석이 정지한 코일 속을 출입할 때 검류계의 바늘이 움직인다. 전류는 자석이 운동하는 동안만 나타나며, 운동이 없을 때는 전류가 나타나지 않는다. 자석을 고정하고 코일을 운동시켜도 같은 결과를 얻는다. 즉 자석과 코일의 상대 운동이 필요하다. 관찰 결과에 의하면 이때 생기는 유도전류의 방향은 자석과 코일의 상대운동을 방해하는 방향이다. 상대운동이 빨라지면 유도전류의 세기는 증가한다.
렌츠의 법칙
유도기전력의 방향은 코일면을 통과하는 자속의 변화를 방해하는 방향으로 나타낸다. 코일에 유도되는 전류는 자석의 상대적인 운동을 방해하고 자석의 운동에너지가 코일의 전기에너지로 전환됐다고 생각할 수 있다.
패러데이 법칙
코일이 둘러싸고 있는 면적이 A이고 자속밀도(자기장의 세기)가 B일 때 이 면을 통과하는 자기력선 수(자속)라 하고 Φ로 나타낸다.
Φ=BA(단위 : Wb)
코일면을 지나는 자속이란, 면에 수직한 자속 밀도와 면적의 곱을 말한다. 코일면의 법선과 자기장이 이루는 각이 θ라면 자속은 Φ =BAcosθ이다.이 모형을 이용해 유도기전력의 방향을 찾을때는 자속의 방향도 고려해야 한다. 유도기전력의 크기는 도선의 감은 수와 자속의 시간 변화율에 비례한다.
자기장 속에서 전류가 흐르는 도선이 받는 힘
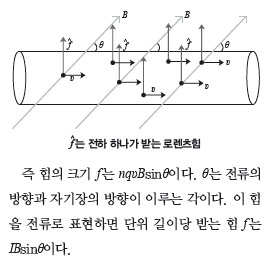
균일한 자기장이 있는 공간에 자기장에 수직인 방향으로 전류가 흐르는 도선을 놓았을 때 전류가 흐르는 도선은 힘을 받는다. 전류와 자기장이 서로 수직일 때 도선이 받는 힘의 크기는 F=BIl의 형태가 된다(B : 자기장의 세기, I : 도선에 흐르는 전류의 세기, l : 도선의 길이).
자기장 속에서 운동하는 전하가 받는 힘
전하가 자기장과 수직인 방향으로 움직이면 힘을 받는다. 이때 전하가 힘을 받는 방향은 자신이 운동하던 방향도 아니고 자기장 방향도 아니다. 두 방향 모두와 수직인 제3의 방향이다. 전하량 Q인 대전 입자가 자기장과 수직한 방향으로 속도 υ로 운동할 때 전하가 받는 자기력의 크기는 F=BQυ (B : 자속 밀도, Q : 전하량, υ : 속도)이다.
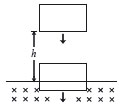1. 다음 그림과 같이 질량이 m(kg), 가로 a(m), 세로 b(m)인 직사각형의 도선이 균일한 자기장으로부터 연직 방향으로 높이 h인 곳에서 자유 낙하하고 있다. 도선의 저항이 R(Ω), 자기장의 세기가 B(T), 중력 가속도가 g(m/s2)이다.1) [난이도 중] 도선이 자기장에 입사하는 순간에 도선에 유도되는 전류의 방향과 세기를 구하시오.
2) [난이도 중] 도선이 자기장에 입사하는 순간부터 등속도로 낙하하기 위한 높이 h를 구하시오.
전문가 클리닉 전자기 유도현상은 회로 내부를 통과하는 자속의 변화에 의해 유도 전류가 발생한다는 페러데이의 입장과 자기장 내에서 운동하는 전하가 받는 힘이 유도기전력으로 나타난다는 로렌츠의 입장에서 모두 설명할 수 있습니다. 로렌츠힘과 전자기 유도현상은 상대운동을 각각 다른 관점에서 볼 때 나타나는 자연스러운 결과입니다. 따라서 전자기 유도와 관련된 문제를 다룰 때는 어떤 관점에서 접근하는 것이 합리적인지 먼저 살펴봐야 합니다.
2) 자기장 내에 들어간 도선에는 왼쪽에서 오른쪽으로 전류가 흐르므로 이 도선은 위쪽 방향으로 힘을 받는다. 이 힘의 크기 F는 BIa=
2. [난이도 상] 전류는 전하의 흐름이다. 따라서 전류가 흐른 도선이 자기장 속에 놓이면, 당연히 힘을 받을 것이다. 전류가 흐르는 방향과 각 θ로 자기장 B가 가해질 때 전하들이 받는 힘으로부터 도선이 받는 힘을 구하시오.
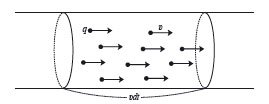
전문가 클리닉 자기장 내에 놓인 전류가 흐르는 도선이 받는 힘은 미시적 관점에서 볼 때 자기장 내에서 움직이는 전하들이 받는 힘의 합입니다. 거시적 세계에서 관측되는 현상들을 미시적 관점으로 분석하면 자연에서 나타나는 규칙성을 파악하는 데 도움될 뿐만 아니라 좀더 근원적인 해석이 가능해집니다.
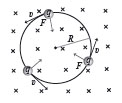3. [난이도 중] 다음 그림처럼 전하 q가 균일한 자기장 속에 수직한 방향으로 속력 υ로 움직일 때, 전하에 작용하는 힘은 전하의 운동방향에 수직이므로 전하의 속력은 변하지 않고 방향만 변하는 등속 원운동을 한다. 이 원운동의 반지름 R과 주기 T를 구하시오.
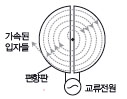전문가 클리닉 균일한 자기장에 수직으로 입사한 전하는 원운동을 합니다. 이때 자기력이 구심력 역할을 합니다. 재미있는 것은 전하의 속력에 따라 회전반경이 따라서 커지지만 회전반경이 커지더라도 회전주기는 변하지 않는다는 사실입니다.이 사실을 이용하면 전하를 가속하는 장치(사이클로트론)를 만들 수 있습니다. 다음 그림처럼 균일한 자기장으로 만들어진 두 개의 반구 사이에 반주기마다 부호가 바뀌는 교류의 전기장을 사이클로트론 진동수에 맞춰 가하면, 하전입자의 에너지를 계속해서 증가시킬 수 있습니다. 그림의 흰 부분 사이(반원판 사이의 갭)에 전기장이 가해지면, 전하의 속력이 커지고, 운동에너지가 증가합니다. 대전된 입자의 원궤도의 반지름이 점점 커지고, 일정한 반지름에 도달하면 가속된 입자가 밖으로 나옵니다.
4. [난이도 하] 지면 뒤쪽을 향하고 있는 균일한 자기장에 대전 입자를 수직하게 입사시켰다. 대전 입자가 그림과 같이 시계 방향으로 궤도 반지름이 감소하는 나선 운동을 하고 있을 때 전자의 운동에 대해 설명하시오.전문가 클리닉 균일한 자기장에 수직으로 입사한 대전입자는 자기장과 속도에 수직한 방향으로 힘을 받습니다. 이때 자기장은 전하의 속력을 변화시키지 않으므로 대전입자는 등속원운동을 합니다. 대전입자가 나선운동을 한다는 것은 속력에 변화가 생겼다는 의미입니다.
예시답안 균일한 자기장에 입사한 대전입자이므로 입자의 속력이 변하지 않는다면 입자는 등속원운동을 해야 한다. 그런데 나선운동을 한다는 것은 시간이 지나면서 대전입자의 속력이 계속 줄어들고 있음을 의미한다. 대전입자의 회전반경이 mυ/qB로 주어지는데 회전반경은 대전입자의 속력에 비례한다. 위의 그림에서는 속력이 일정하게 줄어들면서 회전반경이 점점 작아지는 운동을 하고 있다.
