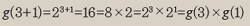호모(homo)라는 단어는 동성애자의 속칭으로 쓰이는 것처럼 ‘같은 종류(the same)’를 뜻하는 접두사다. 수학에서는 하나의 이항연산 구조를 다른 이항연산 구조로 그대로 유지해주는 함수를 말한다. 이항연산이란 덧셈이나 뺄셈처럼 두 항을 연산해 하나의 새로운 항을 만드는 과정이다.
예를 들어 함수 f (x)=7x는 다음 식처럼 덧셈구조를 덧셈구조로 그대로 유지해준다.
즉 식의 왼쪽 편처럼 먼저 덧셈을 한(3 + 11) 다음에 f 를 적용한 결과인 f (3 + 11)이, 오른쪽 편처럼 따로따로 f 를 적용하고(즉 f (3)과 f (11)을 계산해 놓고) 나중에 덧셈을 한 결과인 f (3)+ f (11)과 같다. 덧셈구조를 곱셈구조로 유지해주는 함수도 있다. 함수g(x)=2x 라고 놓자. 그러면
에서 식의 왼쪽 편처럼 먼저 덧셈을 한(즉 3 + 1) 다음에 g를 적용한 3 + 1)과, 오른쪽 편처럼 따로따로 g를 적용하고(즉 g(3)과 g(1)을 계산해 놓고) 나중에 곱셈을 한 g(3)×g(1)이 같은 결과를 준다. 한편 지수함수 대신에 로그함수를 사용하면 곱셈구조를 덧셈구조로 유지해준다.
이런 종류의 함수를 암호에 사용하면 당장 문제점이 생겨난다. 함수 h(x)를 암호에 쓴다고 하자. 비밀정보가 두 개 (x강아지, x야옹이)있을 때 그 정보를 모르더라도 해커는 h (x강아지)=9, h (x야옹이) =8만 알면 “h (x 강아지÷x 야옹이) =9÷8=1.125” 또는 “h(x 강아지-x 야옹이)=9-8=1이구나!”라고 쉽게 추측할 수 있기 때문이다. 이런 방식으로 전자서명까지도 조작할 가능성이 있다.
사람들이 암호를 사용하지 않는 이유 중 하나는 누군가 당신의 개인정보를 볼 수 있다는 점이다. 즉 아무도 모르게 하려고 개인정보를 암호로 바꿨는데 전산 담당자는 그 자료를 마음대로 볼 수 있기 때문이다. 실제로 미국에서는 6개월 동안 1200만 명의 개인 데이터가 해킹당하는 것으로 알려져 있다.
그렇다면 누구도 개인정보 암호를 읽어낼 수 없게 만들면 되지 않을까. 이 경우 예를 들어 지역 주민이 사용한 의료비 총액을 어떻게 계산할 수 있는가 같은 문제가 생긴다.
사실 암호로 저장된 전 국민의 개인의료정보에서 ‘백혈병으로 진단받고 올해 의료보험에서 500만 원 이상 지원받은 사람들이 의료보험공단에서 지원받은 총액’만을 알고 싶을 수도 있다. 그 과정에서 전산담당자가 백혈병 환자의 명단을 알아야 할 이유는 없다.
이렇게 암호화된 상태의 자료를 가지고 암호를 풀지 않고, 즉 당사자 이외에는 아무도 암호문의 실제 내용이 무엇인지 모르는 상태에서, 암호문 자체만을 갖고 각종 계산을 해서 여러 가지 정보를 뽑아낼 수 있으면 누구나 만족할 것이다.
30년 만에 난제 풀어
{cIMG_l4}수학자들은 지난 30년 동안 이렇게 작동하는 암호 체계를 찾으려고 했지만 번번이 실패했다. 그런데 최근 미국 스탠퍼드대 전산학과의 크랙 젠트리 박사가 암호를 읽어내지 않고도 각종 계산을 가능하게 해주는 암호를 발견해 화제다. 젠트리 박사는 대학에서는 수학과를 졸업하고, 하버드대 법대를 나와 한동안 변호사 생활을 했다. 따분한 법률업무에 싫증난 그는 자신의 수학 전공을 어필해 일본계 정보통신 회사에서도 몇 년간 일했던 특이한 경력을 갖고 있다. 이때 처음 암호학을 접하고 흥미를 갖게 됐다. 그 뒤 젠트리 박사는 스탠퍼드대에 들어갔고 2008년 여름 IBM에서 3개월 인턴으로 일하는 도중 뉴욕의 한 카페에서 이 암호를 발견했다. 물론 IBM은 그를 정사원으로 채용했다.
사실 IBM은 예전에 이와 비슷한 암호를 개발했었다. 이 암호는 동일한 원문을 사용해도 암호문이 조금씩 변하게 설계됐는데 덧셈구조를 상당히 유지해주는 암호였다. 앞의 예를 사용하면, h(x 강아지)=9.2, h(x야옹이)=8.1일 경우, 때에 따라 h(x강아지-x야옹이)이 1.3으로 나올 수도 있고 1.0으로 나올 수도 있다. 현재 널리 쓰이는
암호체계는 늘 9.2 - 8.1 = 1.1 이 나온다. 따라서 원문(x강아지, x야옹이)에 무의미한 내용을 덧붙여서 암호문을 만든다. 결국 이렇게 만든 암호로 연산을 하려면 암호를 푼 뒤 원문을 복원해야 한다.
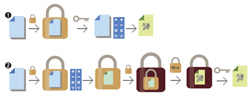
IBM의 암호 체계는 원문은 그대로이면서 암호문이 조금씩 바뀌기 때문에 해커들이 원문의 실체를 눈치채지 못하게 하면서 반복적으로 쓸 수 있다. 그런데 문제는 이런 근삿값을 반복하면 점점 원래 값에서 멀어져 궁극적으로 합법적인 사용자조차 원래 값을 잃어버리게 된다는 점이다.
젠트리 박사는 이런 암호 중 추가로 곱셈구조까지 상당히 유지해주는 암호를 찾아내 그 문제를 해결했다. 즉 근삿값을 주는 연산을 무한히 반복해도 원래 값에 벗어나지 않는다. 만일 암호 체계가덧셈과 곱셈구조를 유지한다면 암호화된 데이터를 해독하지 않은 채 어떤 계산이라도 할 수 있게 된다. 그는 이 방법이 마치 환자가 옷을 벗지 않은 채 수술을 받는 것과 같다고 비유했다.
아쉽게도 젠트리 박사의 암호 체계를 바로 적용하기는 어렵다. 새로운 알고리듬은 엄청난 계산량을 필요하기 때문이다. 즉 이 방법을 쓰면 암호를 해독해 데이터를 계산하는 경우보다 1억 배 정도로 시간이 더 든다. 물론 새로운 개념이 나타났을 때 실용화까지는 아득해 보이는 경우가 많다. 그러나 많은 연구자들이 속도향상에 뛰어들면 언젠가는 현재의 암호 체계를 대체할 수 있는 날이 올 것이다.