구독상품안내
과학영재학교와 과학고 입시에서 창의적 문제해결력 검사의 비중이 커지고 문제 유형 또한 바뀌고 있다. 출제가능성이 높은 예상문제를 풀어봄으로써 실전감각을 길러두자.
1. 1 x, y 100이고 x와 y를 이 범위 안에서 각각 임의로 뽑는다고 할 때 다음 물음에 답하라.
1) 5x+7y의 값이 4의 배수가 될 확률은 얼마인가?
2) 5x+6y=n을 만족하는 확률이 이 되도록 하는 n의 최소값은 얼마인가?
1) 5x+7y=5x-y+8y이므로 5x-y=4k 꼴이면 5x+7y는 4의 배수이다. 단 k는 정수여야 하고 음의 정수라도 상관없다. 즉 y=5x-4k 형태인데 5x를 4로 나눈 나머지가 0, 1, 2, 3인 각 경우에 대해 k를 바꾸면 가능한 y값을 알 수 있다. 예를 들어 x=15이면 5x=75를 4로 나눈 나머지가 3인데, k=18일 때 y=3이고 k가 점점 작아져 k=-6일 때 y=99가 된다. 따라서 5x+7y가 4의 배수를 만족하는 y값은 3, 7, …, 95, 99이다.
각각의 x값에 대해 5x+7y가 4의 배수인 y값이 25개 존재하므로 5x+7y가 4의 배수를 만족하는 (x, y)쌍은 2500개이며 확률은 2500/100×100=1/4이다.
2) 1≤ x, y≤100에서 전체 경우의 수가 10000가지이므로 5x+6y=n을 만족하는 경우가 3이 되도록 n값을 결정한다. 먼저 5x+6y=1의 해를 구하면 x=-1, y=1이다. 이로부터 5x+6y=n은 x=-n, y=n일 때 성립함을 알 수 있다. 또 x가 6씩 늘어나고 y가 5씩 줄어들면 5x+6y 값은 변화가 없으므로 5x+6y=n의 해는 x=6t-n, y=n-5t이다. x, y 모두 0보다 커야 하므로 6t-n＞0, n-5t＞0에서 n＜t＜n가 성립한다. 이 식을 만족하는 정수 t가 3개 존재해야 하므로 1/5n-1/6n＞2가 된다. 따라서 n＞60이어야 하는데 n=61이면 1/6n＜t＜1/5n를 만족하는 t가 2개뿐이므로 조건에 맞지 않는다. t의 개수가 늘어나려면 1/5n에서 정수부분이 커져야 하므로 n=66을 대입해도 식을 만족하는 t는 2개뿐이다. 다시 n을 5만큼 늘려 n=71을 대입하면 1/6n＜t＜1/5n를 만족하는 t가 3개 존재하고 x, y 모두 100이하라는조건을 만족시킨다. 따라서 n의 최소값은 71이다.
2. 다음 물음에 답하라.
1) 갑과 을이 1시에서 2시 사이에 역에서 만나기로 했다. 두 명 모두 약속장소에 도착한 뒤 상대방이 올 때까지 10분간 기다린다고 할 때 갑과 을이 만날 확률은 얼마인가?
2) 갑, 을, 병이 1시에서 2시 사이에 역에서 만나기로 했다. 병은 1시 10분에서 1시 50분 사이에 역에 도착한다. 세 명 모두 약속장소에 도착한 뒤 상대방이 올 때까지 10분간 기다린다고 할 때 갑, 을, 병이 모두 만날 확률은 얼마인가?
예시답안
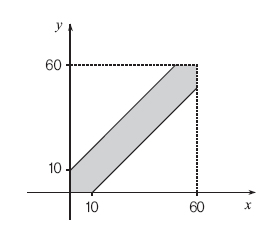
1) 갑이 1시 x분, 을이 1시 y분에 도착한다고 하면 0≤x, y≤60이고 |x-y| 10일 때 갑과 을이 만난다. xy평면에 갑과 을이 만나는 경우를 표현하면 그림과 같다.
0≤x, y≤60에서 x, y가 존재하는 영역의 넓이는 3600이고 갑과 을이 만나는 영역의 넓이는 3600-2×1/2 502=1100이다. 따라서 갑과 을이 만날 확률은 11/36이다.
2) 갑이 1시 x분, 을이 1시 y분, 병이 1시 z분에 도착한다고 하면 0≤x, y≤60, 10≤x≤50이고 |x-y|≤10, |y-z|≤10, |z-x|≤10일 때 갑, 을, 병이 모두 만난다. z=k일 때 xy평면에 갑, 을, 병이 모두 만나는 경우를 표현하면 그림과 같다.
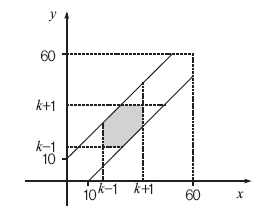
주어진 조건에서 x, y, z가 존재하는 영역의 부피는 60×60×40=144000이다. 갑, 을, 병이 모두 만나는 영역은 단면 넓이가 300, 높이가 40인 기울어진 사각기둥으로 부피가 12000이다. 따라서 갑, 을, 병이 모두 만날 확률은 12/144=1/12이다.
과학
1. 기체의 용해도에 대한 다음 물음에 답하라.
1) 0°C, 1기압에서 물 500g에 녹을 수 있는 산소의 부피는 15mL이다. 0°C, 3기압에서 물 100g에 녹을 수 있는 산소의 부피는 얼마인가?
2) 0°C, 5기압에서 물 200g에 산소를 최대한 녹인 뒤 뚜껑을 닫았다. 40°C, 1기압에서 용액의 뚜껑을 열었더니 산소기체가 발생했다. 이때 발생한 산소의 질량은 얼마인가? (단 산소의 물에 대한 용해도는 0°C, 1기압에서 0.335이고 40°C, 1기압에서 0.160이다.)
예시답안
1) 헨리의 법칙에 의하면 일정한 양의 물에 대해 압력이 증가할 때 용해되는 기체의 질량은 증가하지만 부피는 일정하다. 따라서 압력이 1기압에서 3기압으로 증가해도 용해되는 산소의 부피는 변화가 없다. 물의 양이 1/5배 감소했으므로 용해되는 산소의 부피도 1/5배 줄어들어 0℃, 3기압에서 물 100g에 용해될 수 있는 산소의 부피는 3mL이다.
2) 산소가 0°C, 1기압에서 물 100g에는 0.335g이 녹으므로, 물 200g에는 0.335g×2=0.67g이 녹는다. 기체의 용해도는 압력에 비례하므로 압력을 1기압에서 5기압으로 증가시키면 용해도도 5배 증가한다. 0℃, 5기압에서 용해되는 산소의 질량은 0.67g×5=3.35g이다. 이 용액의 온도를 40℃로 증가시키고 압력을 1기압으로 하면, 물 200g에 용해되는 산소 기체의 질량은 0.16g×2=0.32g이다. 그러므로 발생하는 산소의 질량은 3.35g-0.32g=3.03g이다.
2. 영희는 그림과 같이 1M HCl용액 50mL를 만들어서 실험을 하고자 한다. 다음 물음에 답하라.
1) 35% 진한 염산을 이용해 1M HCl 50mL 만드는 방법을 설명하라.
2) 탄산칼슘(CaCO3)을 물에 용해시켰을 때 액성을 판단하고 그 이유를 설명하라.
3) 용액 (가)에 탄산칼슘을 첨가할 때 일어나는 화학반응식을 완성하고, 발생하는 기체를 확인할 수 있는 방법을 설명하라.
3. 다음 그림은 헤모글로빈을 구성하는 글로빈이 발생 과정 중에 만들어지는 장소, 종류, 빈도를 나타낸 것이다.
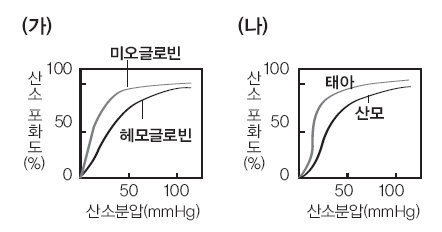
그래프 (가)는 헤모글로빈과 미오글로빈의 산소해리곡선을, 그래프 (나)는 산모와 태아에서 헤모글로빈의 산소해리곡선을 나타낸 것이다.(단 미오글로빈은 근육에서 산소를 저장하는 역할을 하는 단백질이다.)
1) 헤모글로빈은 4개의 폴리펩티드로 돼 있다. 다음 시기에 나타나는 헤모글로빈의 주된 형태는 무엇인가?
① 태아기 ② 생후 6개월 후
2) 태아기와 생후 6개월 후에 나타나는 혈구세포는 주로 어디에서 만들어지는가?
① 태아 초기 ② 생후 6개월 후
3) 태아기에 나타나는 헤모글로빈과 출생 후 헤모글로빈 형태의 산소친화력을 비교하고 친화력에서 차이가 나는 원인을 산소포화도와 관련지어 설명하라.
4) 헤모글로빈과 미오글로빈의 산소친화력을 비교하고 친화력의 차이가 뜻하는 바를 설명하라.
5) 미오글로빈에 산소가 결합만 돼 있으면 세포호흡에 산소를 이용할 수 없는데 이러한 문제는 어떻게 해결하는지 그래프 (가)를 보고 설명하라.
예시답안
1) ① 태아기 : α2γ2
② 생후 6개월 후 : α2β2
2) ① 태아 초기 : 간 ② 생후 6개월 후 : 골수
3) 태아기에 나타나는 헤모글로빈이 같은 산소분압일 때 산소포화도가 더 높게 나타나는 점으로 볼 때 산소친화력이 훨씬 더 높다. 이는 모체로부터 오는 산소를 태반을 통해 받아들여 호흡을 해야 하기 때문에 모체가 갖는 즉, 출산 후에 나타나는 헤모글로빈 형태보다 산소에 대한 친화력이 높다.
4) 그래프 (가)에서 산소분압이 같을 때 미오글로빈이 헤모글로빈보다 산소포화도가 높다. 그러므로 헤모글로빈이 운반해 온 산소는 근육에서 미오글로빈으로 전해져 저장된다.
5) 근육세포 내에서 산소가 세포호흡에 이용되려면 미오글로빈에 결합돼 있던 산소가 해리돼야 하는데, 그래프 (가)에서 산소분압이 20mmHg보다 낮아질 때 미오글로빈의 산소포화도가 크게 감소한다. 따라서 심한 운동으로 근육 내 산소분압이 크게 낮아지면 미오글로빈에 저장돼 있던 산소가 대량으로 해리돼 나와 세포호흡에 이용된다.
4. 다음 그림은 우리나라의 어느 지점(위도 36°N)에서 12월 1일부터 12월 31일까지 달의 남중시각을 나타낸 것이다. 물음에 답하라.
1) 보름달이 뜨는 날은 언제인가?
2) 만일 달의 공전궤도면과 지구의 공전궤도면이 일치한다면 보름달이 뜨는 날, 달의 남중고도를 구하라.
예시답안
1) 보름달은 초저녁에 떠서 한밤중에 남중하므로 남중시각이 24시인 12월 21일이 보름달이 뜨는 날이다.
2) 다음 그림처럼 같은 날 낮(③)과 밤(④)의 지평선 방향은 반대가 되는데, 북극성 별빛 즉 지구 자전축을 중심으로 같은 각도(그 지역의 위도: φ)를 이루며 기울어져 있다. 12월 21일은 24절기 중 동지를 나타내고 동지 때 태양은 천구의 적도보다 23.5° 아래쪽에 놓인다. 달과 지구의 공전궤도면이 일치한다고 가정했으므로 달은 같은 면의 태양 반대쪽에 놓인다. 그림에서 밤의 지평선(④)과 달이 이루는 각인 보름달의 남중고도(h′)는 90°-φ+23.5°임을 알 수 있다. 그러므로 보름달의 남중고도는 77.5°이다.
φ : 북극성의 고도=그 지역의 위도
① : 천구의 적도 ② : 황도
③ : 낮의 지평선 ④ : 밤의 지평선
5. 질량이 각각 4kg과 3kg인 두 추 A와 B를 그림과 같이 도르래에 걸어 놓고 추 B를 잡고 있다가 놓았다. 물체 A, B의 가속도와 실에 걸리는 장력의 크기를 각각 구하라. (단 중력가속도는 10m/s2이며 두 도르래와 줄의 질량 그리고 모든 마찰은 무시한다.)
6. 다음 그림은 인접해 있는 A~C 세 지역의 지층 단면도이다. 물음에 답하라.
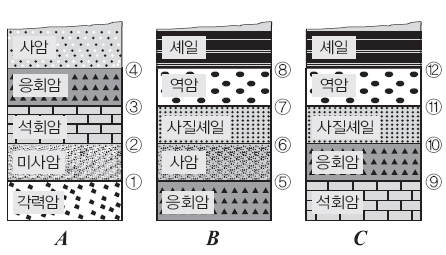
1) 그림에 나타난 모든 지층에서 과거에 역전된 흔적이 발견되지 않았을 때 각 암석들을 가장 오래전에 생성된 순서대로 나열하라.
2) 세 지층 가운데 부정합이 존재할 가능성이 있는 층을 고르고, 부정합면이 될 수 있는 곳을 써라.
예시답안
1) 지층들이 쌓인 시기를 비교할 수 있는 기준층은 응회암층이다. 응회암은 화산재가 쌓여 만들어진 퇴적암으로 화산활동이 일어날 때만 만들어진다. 세 지역의 응회암층은 모두 같은 시기에 형성됐기 때문에 이 층을 중심으로 지층의 생성시기를 비교한다. 응회암의 가장 아래쪽에 있는 지층 A의 각력암이 가장 오래된 암석이며, 응회암의 가장 위에 있는 셰일이 가장 최근의 암석이다. 따라서 각력암-미사암-석회암-응회암-사암-사질셰일-역암-셰일 순이다.
2) 지층 C는 응회암과 사질셰일 사이의 사암이 없다는 점에서 지층이 깎여 나간 부정합이 존재할 가능성이 있다. 그러므로 부정합 면이 될 수 있는 곳은 응회암과 사질셰일 사이의 경계인 지층 C의 ⑩번이다. 부정합 면은 지질시대를 구분하는 기준으로 쓰이기도 한다.
1. 1 x, y 100이고 x와 y를 이 범위 안에서 각각 임의로 뽑는다고 할 때 다음 물음에 답하라.
1) 5x+7y의 값이 4의 배수가 될 확률은 얼마인가?
2) 5x+6y=n을 만족하는 확률이 이 되도록 하는 n의 최소값은 얼마인가?
1) 5x+7y=5x-y+8y이므로 5x-y=4k 꼴이면 5x+7y는 4의 배수이다. 단 k는 정수여야 하고 음의 정수라도 상관없다. 즉 y=5x-4k 형태인데 5x를 4로 나눈 나머지가 0, 1, 2, 3인 각 경우에 대해 k를 바꾸면 가능한 y값을 알 수 있다. 예를 들어 x=15이면 5x=75를 4로 나눈 나머지가 3인데, k=18일 때 y=3이고 k가 점점 작아져 k=-6일 때 y=99가 된다. 따라서 5x+7y가 4의 배수를 만족하는 y값은 3, 7, …, 95, 99이다.
각각의 x값에 대해 5x+7y가 4의 배수인 y값이 25개 존재하므로 5x+7y가 4의 배수를 만족하는 (x, y)쌍은 2500개이며 확률은 2500/100×100=1/4이다.
2) 1≤ x, y≤100에서 전체 경우의 수가 10000가지이므로 5x+6y=n을 만족하는 경우가 3이 되도록 n값을 결정한다. 먼저 5x+6y=1의 해를 구하면 x=-1, y=1이다. 이로부터 5x+6y=n은 x=-n, y=n일 때 성립함을 알 수 있다. 또 x가 6씩 늘어나고 y가 5씩 줄어들면 5x+6y 값은 변화가 없으므로 5x+6y=n의 해는 x=6t-n, y=n-5t이다. x, y 모두 0보다 커야 하므로 6t-n＞0, n-5t＞0에서 n＜t＜n가 성립한다. 이 식을 만족하는 정수 t가 3개 존재해야 하므로 1/5n-1/6n＞2가 된다. 따라서 n＞60이어야 하는데 n=61이면 1/6n＜t＜1/5n를 만족하는 t가 2개뿐이므로 조건에 맞지 않는다. t의 개수가 늘어나려면 1/5n에서 정수부분이 커져야 하므로 n=66을 대입해도 식을 만족하는 t는 2개뿐이다. 다시 n을 5만큼 늘려 n=71을 대입하면 1/6n＜t＜1/5n를 만족하는 t가 3개 존재하고 x, y 모두 100이하라는조건을 만족시킨다. 따라서 n의 최소값은 71이다.
2. 다음 물음에 답하라.
1) 갑과 을이 1시에서 2시 사이에 역에서 만나기로 했다. 두 명 모두 약속장소에 도착한 뒤 상대방이 올 때까지 10분간 기다린다고 할 때 갑과 을이 만날 확률은 얼마인가?
2) 갑, 을, 병이 1시에서 2시 사이에 역에서 만나기로 했다. 병은 1시 10분에서 1시 50분 사이에 역에 도착한다. 세 명 모두 약속장소에 도착한 뒤 상대방이 올 때까지 10분간 기다린다고 할 때 갑, 을, 병이 모두 만날 확률은 얼마인가?
예시답안
1) 갑이 1시 x분, 을이 1시 y분에 도착한다고 하면 0≤x, y≤60이고 |x-y| 10일 때 갑과 을이 만난다. xy평면에 갑과 을이 만나는 경우를 표현하면 그림과 같다.
0≤x, y≤60에서 x, y가 존재하는 영역의 넓이는 3600이고 갑과 을이 만나는 영역의 넓이는 3600-2×1/2 502=1100이다. 따라서 갑과 을이 만날 확률은 11/36이다.
2) 갑이 1시 x분, 을이 1시 y분, 병이 1시 z분에 도착한다고 하면 0≤x, y≤60, 10≤x≤50이고 |x-y|≤10, |y-z|≤10, |z-x|≤10일 때 갑, 을, 병이 모두 만난다. z=k일 때 xy평면에 갑, 을, 병이 모두 만나는 경우를 표현하면 그림과 같다.
주어진 조건에서 x, y, z가 존재하는 영역의 부피는 60×60×40=144000이다. 갑, 을, 병이 모두 만나는 영역은 단면 넓이가 300, 높이가 40인 기울어진 사각기둥으로 부피가 12000이다. 따라서 갑, 을, 병이 모두 만날 확률은 12/144=1/12이다.
과학
1. 기체의 용해도에 대한 다음 물음에 답하라.
1) 0°C, 1기압에서 물 500g에 녹을 수 있는 산소의 부피는 15mL이다. 0°C, 3기압에서 물 100g에 녹을 수 있는 산소의 부피는 얼마인가?
2) 0°C, 5기압에서 물 200g에 산소를 최대한 녹인 뒤 뚜껑을 닫았다. 40°C, 1기압에서 용액의 뚜껑을 열었더니 산소기체가 발생했다. 이때 발생한 산소의 질량은 얼마인가? (단 산소의 물에 대한 용해도는 0°C, 1기압에서 0.335이고 40°C, 1기압에서 0.160이다.)
예시답안
1) 헨리의 법칙에 의하면 일정한 양의 물에 대해 압력이 증가할 때 용해되는 기체의 질량은 증가하지만 부피는 일정하다. 따라서 압력이 1기압에서 3기압으로 증가해도 용해되는 산소의 부피는 변화가 없다. 물의 양이 1/5배 감소했으므로 용해되는 산소의 부피도 1/5배 줄어들어 0℃, 3기압에서 물 100g에 용해될 수 있는 산소의 부피는 3mL이다.
2) 산소가 0°C, 1기압에서 물 100g에는 0.335g이 녹으므로, 물 200g에는 0.335g×2=0.67g이 녹는다. 기체의 용해도는 압력에 비례하므로 압력을 1기압에서 5기압으로 증가시키면 용해도도 5배 증가한다. 0℃, 5기압에서 용해되는 산소의 질량은 0.67g×5=3.35g이다. 이 용액의 온도를 40℃로 증가시키고 압력을 1기압으로 하면, 물 200g에 용해되는 산소 기체의 질량은 0.16g×2=0.32g이다. 그러므로 발생하는 산소의 질량은 3.35g-0.32g=3.03g이다.
2. 영희는 그림과 같이 1M HCl용액 50mL를 만들어서 실험을 하고자 한다. 다음 물음에 답하라.
1) 35% 진한 염산을 이용해 1M HCl 50mL 만드는 방법을 설명하라.
2) 탄산칼슘(CaCO3)을 물에 용해시켰을 때 액성을 판단하고 그 이유를 설명하라.
3) 용액 (가)에 탄산칼슘을 첨가할 때 일어나는 화학반응식을 완성하고, 발생하는 기체를 확인할 수 있는 방법을 설명하라.
3. 다음 그림은 헤모글로빈을 구성하는 글로빈이 발생 과정 중에 만들어지는 장소, 종류, 빈도를 나타낸 것이다.
그래프 (가)는 헤모글로빈과 미오글로빈의 산소해리곡선을, 그래프 (나)는 산모와 태아에서 헤모글로빈의 산소해리곡선을 나타낸 것이다.(단 미오글로빈은 근육에서 산소를 저장하는 역할을 하는 단백질이다.)
1) 헤모글로빈은 4개의 폴리펩티드로 돼 있다. 다음 시기에 나타나는 헤모글로빈의 주된 형태는 무엇인가?
① 태아기 ② 생후 6개월 후
2) 태아기와 생후 6개월 후에 나타나는 혈구세포는 주로 어디에서 만들어지는가?
① 태아 초기 ② 생후 6개월 후
3) 태아기에 나타나는 헤모글로빈과 출생 후 헤모글로빈 형태의 산소친화력을 비교하고 친화력에서 차이가 나는 원인을 산소포화도와 관련지어 설명하라.
4) 헤모글로빈과 미오글로빈의 산소친화력을 비교하고 친화력의 차이가 뜻하는 바를 설명하라.
5) 미오글로빈에 산소가 결합만 돼 있으면 세포호흡에 산소를 이용할 수 없는데 이러한 문제는 어떻게 해결하는지 그래프 (가)를 보고 설명하라.
예시답안
1) ① 태아기 : α2γ2
② 생후 6개월 후 : α2β2
2) ① 태아 초기 : 간 ② 생후 6개월 후 : 골수
3) 태아기에 나타나는 헤모글로빈이 같은 산소분압일 때 산소포화도가 더 높게 나타나는 점으로 볼 때 산소친화력이 훨씬 더 높다. 이는 모체로부터 오는 산소를 태반을 통해 받아들여 호흡을 해야 하기 때문에 모체가 갖는 즉, 출산 후에 나타나는 헤모글로빈 형태보다 산소에 대한 친화력이 높다.
4) 그래프 (가)에서 산소분압이 같을 때 미오글로빈이 헤모글로빈보다 산소포화도가 높다. 그러므로 헤모글로빈이 운반해 온 산소는 근육에서 미오글로빈으로 전해져 저장된다.
5) 근육세포 내에서 산소가 세포호흡에 이용되려면 미오글로빈에 결합돼 있던 산소가 해리돼야 하는데, 그래프 (가)에서 산소분압이 20mmHg보다 낮아질 때 미오글로빈의 산소포화도가 크게 감소한다. 따라서 심한 운동으로 근육 내 산소분압이 크게 낮아지면 미오글로빈에 저장돼 있던 산소가 대량으로 해리돼 나와 세포호흡에 이용된다.
4. 다음 그림은 우리나라의 어느 지점(위도 36°N)에서 12월 1일부터 12월 31일까지 달의 남중시각을 나타낸 것이다. 물음에 답하라.
1) 보름달이 뜨는 날은 언제인가?
2) 만일 달의 공전궤도면과 지구의 공전궤도면이 일치한다면 보름달이 뜨는 날, 달의 남중고도를 구하라.
예시답안
1) 보름달은 초저녁에 떠서 한밤중에 남중하므로 남중시각이 24시인 12월 21일이 보름달이 뜨는 날이다.
2) 다음 그림처럼 같은 날 낮(③)과 밤(④)의 지평선 방향은 반대가 되는데, 북극성 별빛 즉 지구 자전축을 중심으로 같은 각도(그 지역의 위도: φ)를 이루며 기울어져 있다. 12월 21일은 24절기 중 동지를 나타내고 동지 때 태양은 천구의 적도보다 23.5° 아래쪽에 놓인다. 달과 지구의 공전궤도면이 일치한다고 가정했으므로 달은 같은 면의 태양 반대쪽에 놓인다. 그림에서 밤의 지평선(④)과 달이 이루는 각인 보름달의 남중고도(h′)는 90°-φ+23.5°임을 알 수 있다. 그러므로 보름달의 남중고도는 77.5°이다.
φ : 북극성의 고도=그 지역의 위도
① : 천구의 적도 ② : 황도
③ : 낮의 지평선 ④ : 밤의 지평선
5. 질량이 각각 4kg과 3kg인 두 추 A와 B를 그림과 같이 도르래에 걸어 놓고 추 B를 잡고 있다가 놓았다. 물체 A, B의 가속도와 실에 걸리는 장력의 크기를 각각 구하라. (단 중력가속도는 10m/s2이며 두 도르래와 줄의 질량 그리고 모든 마찰은 무시한다.)6. 다음 그림은 인접해 있는 A~C 세 지역의 지층 단면도이다. 물음에 답하라.
1) 그림에 나타난 모든 지층에서 과거에 역전된 흔적이 발견되지 않았을 때 각 암석들을 가장 오래전에 생성된 순서대로 나열하라.
2) 세 지층 가운데 부정합이 존재할 가능성이 있는 층을 고르고, 부정합면이 될 수 있는 곳을 써라.
예시답안
1) 지층들이 쌓인 시기를 비교할 수 있는 기준층은 응회암층이다. 응회암은 화산재가 쌓여 만들어진 퇴적암으로 화산활동이 일어날 때만 만들어진다. 세 지역의 응회암층은 모두 같은 시기에 형성됐기 때문에 이 층을 중심으로 지층의 생성시기를 비교한다. 응회암의 가장 아래쪽에 있는 지층 A의 각력암이 가장 오래된 암석이며, 응회암의 가장 위에 있는 셰일이 가장 최근의 암석이다. 따라서 각력암-미사암-석회암-응회암-사암-사질셰일-역암-셰일 순이다.
2) 지층 C는 응회암과 사질셰일 사이의 사암이 없다는 점에서 지층이 깎여 나간 부정합이 존재할 가능성이 있다. 그러므로 부정합 면이 될 수 있는 곳은 응회암과 사질셰일 사이의 경계인 지층 C의 ⑩번이다. 부정합 면은 지질시대를 구분하는 기준으로 쓰이기도 한다.
