d라이브러리

아이스 댄싱 경기에서 선수가 회전하는 일은 흔하다. 미끄러져 가다가 몸을 틀면서 돌기 시작하는 선수는 회오리처럼 보인다. 속도를 높이면 마치 고치처럼 둥그스름해진다.

이렇듯 회전하는 물체는 둥근 모양을 만든다. 삼각형을 회전시키면 원뿔이 생기고 직사각형은 원기둥이 생긴다. 송곳이나 드릴을 이용해서 구멍을 뚫으면 둥근 구멍이 생기는 것은 당연하다.

그렇다면 사각형 모양의 구멍을 뚫을 수 있는 드릴은 만들 수 없을까. 실제로 그런 드릴은 한 공학자에 의해 20세기 초반에 발명됐다. 그 주인공은 영국인 해리 와트. 그가 만든 드릴은 과연 어떤 것일까.
 

먼저 사각형 모양의 구멍을 뚫을 수 있으려면 드릴의 모양이 어떠해야 할지를 생각해보자. 이를 위해 우선 임의의 모양으로 생긴 도형이 있다고 가정하자. 이 도형을 어느 한 방향에서 수직으로 그림자를 비춰보자. 그 결과 생긴 선분의 길이는 방향에 따라 어떻게 달라질까.

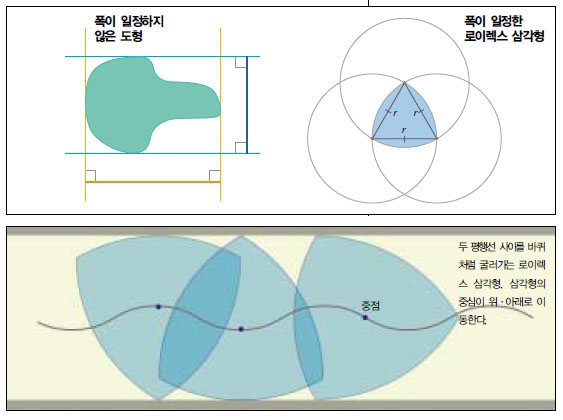
만약 도형이 원이라면 어느 방향에서나 그림자의 길이는 모두 원의 지름으로 똑같다. 원처럼 어느 방향으로나 그림자의 길이가 같은 것을 ‘폭이 일정한 도형’이라고 한다. 삼각형이나 사각형은 폭이 일정한 도형이 아니다.

그렇다면 원은 아니면서도 폭이 일정한 도형은 없을까. 정삼각형을 그려보자. 그리고 한 꼭지점을 중심으로 하고 나머지 두개의 꼭지점을 지나는 원을 각 꼭지점마다 그린다. 이 결과 얻어지는 세 원이 모두 겹치는 영역만을 오려낸다.

이 도형은 원처럼 어느 방향으로나 폭이 일정하다. 이같은 도형은 독일 공학자 프란츠 로이렉스가 19세기에 처음 만들어냈다. 때문에 ‘로이렉스 삼각형’이라고 불린다.

로이렉스 삼각형은 폭이 일정하므로 두 평행선 사이를 바퀴처럼 굴러갈 수 있다. 이때 두 평행선 사이의 거리는 로이렉스 삼각형의 폭과 같다. 벌목장 같은 곳에서 여러개의 통나무를 늘어놓고 컨베이어 벨트처럼 쓰는 일이나, 폭이 일정한 원 모양으로 마차의 바퀴를 만드는 것과 같은 이치다.


사각형 안에 갇힌 로이렉스 삼각형

그런데 만약 이 평행선과 수직한 또다른 평행선 쌍을 만들어 놓으면 어떻게 될까. 평행선 사이의 거리가 로이렉스 삼각형의 폭과 같다면 이 도형은 평행선 사이를 바퀴처럼 굴러갈 것이다. 따라서 평행선 두쌍이 서로 수직으로 만나는 경우에는 정사각형 안에서 움직이게 될 것이다. 그리고 로이렉스 삼각형은 꼭지점 부분 약간을 제외한 정사각형의 모든 영역을 지나갈 수 있다.

이제 로이렉스 삼각형에 칼날을 붙인다. 그러면 로이렉스 삼각형이 회전하면서 사각형 모양의 구멍이 뚫리게 된다. 이것이 바로 와트가 로이렉스의 삼각형을 이용해서 만든 사각 드릴이다. 이처럼 새로운 시도는 늘 그렇듯이 기존의 관념을 깨는데서 출발한다.

이 드릴의 또다른 비밀은 어디에 있을까. 바로 회전축이 고정돼 있지 않다는 사실에 있다. 만약 회전축이 고정돼 있다면 당연히 로이렉스 삼각형이 회전해서 얻을 수 있는 모양은 원이다. 보통의 드릴은 회전축이 고정돼 있지만 이 드릴에서는 회전축이 사각형의 중심을 주위로 이동한다.

사각 구멍을 뚫을 수 있다면 오각형, 육각형 모양의 구멍도 뚫을 수 있지 않을까. 그렇다. 로이렉스 삼각형을 만들었던 방법을 그대로 정사각형에 적용시킨다. 그러면 오각형을 뚫을 수 있는 드릴의 모양을 만들 수 있다. 정오각형 모양의 폭이 일정한 도형으로 드릴을 만들면 정육각형 모양의 구멍을 뚫을 수 있다.

폭이 일정한 도형은 사각이나 오각 구멍을 뚫는 드릴에만 이용되는 것이 아니다. 로이렉스 삼각형은 영사기에 쓰이는데, 여러 장이 연속으로 붙어있는 필름이 서로 겹치지 않으면서 각장이 제대로 보이게 하기 위해서다. 로이렉스 삼각형의 폭을 필름 길이에 맞추고 이 삼각형을 회전시키면, 필름이 겹치지 않고 한장씩 차례로 보이게 된다.