d라이브러리

과거 남한에서도 성행한 서커스.현재는 서커스단이 거의 남아있지 않다.그러나 북한에는 세계 최정상의 서커스단이 있다.이름하여 평양교예단.이를 본 사람들은 한 목소리로 정말 대단하다고 평가하는데….이 속에 숨은 과학적 원리는?

반∼갑습네다. 반갑습네다.” “세계 최정상의 평양교예단의 공연을 재미나게 보러 와 주신 독자여러분 반갑습네다.”
역사적인 남북정상회담을 앞두고 관심을 집중시킨 세계 정상급의 평양교예단의 서울공연. 여느 서커스와는 달리 정감 어린 모습이었다. 이들이 보여준 환상적인 묘기를 보는 관람객들은 평양교예단과 함께 긴장하고 웃을 수 있었다.
관람객이 흥미롭게 지켜보면서 탄성을 자아내게 한 평양교예단의 기교들. 이 속에 어떤 과학적 원리가 숨어있는 것일까.
“평양교예단의 실력이 왜 최정상인지 압네까?”

장대타기:공중에서 옆으로 누운자세

세워진 장대에 올라가 공중에서 두팔로 장대를 잡고 몸을 옆으로 누운 자세로 유지하는 ‘장대타기’ 기교를 먼저 살펴보자. 보통사람이 아무 기둥이나 잡고 흉내를 내보려고 해도 비슷하게 조차도 따라할 수 없다. 장대타기의 연기자는 어떻게 이런 자세를 보여줄 수 있을까.

물체가 정지상태에서 그대로 있으려면 그 물체에 작용하는 여러 힘들이 평형을 이뤄야 한다. 즉 사람의 몸이 공중에 떠서 멈춰있으려면, 이 사람에게 작용하는 힘들을 합했을 때 0이 된다는 말이다. 그렇다면 이 사람에게 어떤 힘들이 작용하는 것일까.

가장 쉽게 떠오르는 것이 중력일 것이다. 장대타기를 보여주는 사람의 몸무게가 70kg, 장대로부터 그 사람의 무게중심까지 90cm, 벌린 두팔 사이의 거리가 1백20cm라고 해보자. 중력가속도를 10m/${초}^{2}$이라면 이 사람이 받는 중력은 아래방향으로 7백N(중력=질량×중력가속도=70kg×10m/${초}^{2}$=7백N)이다. 그렇다면 아래방향으로 작용하는 7백N의 중력을 상쇄하기 위해 위방향의 힘이 어디선가 작용해야 한다.

어디에서 힘이 작용하는 것일까. 아무리 살펴봐도 장대를 잡고 있는 두손밖에 없다. 두손에는 몸을 아래로 내려가도록 하는 중력을 이기기 위해 위방향으로 힘이 작용한다. 만약 두손에 작용하는 힘이 같다면 그 값은 각각 3백50N이 된다.

그렇다면 단지 두손에 몸이 아래로 내려가려는 중력을 이기는 힘이 작용하면 이 자세가 만들어지는 것일까. 아니다. 만약 이 상태라면 몸은 반시계방향으로 회전해서 다리가 땅으로 내려오고 만다. 마치 진자가 최고점에서 아래로 내려오는 것처럼. 따라서 힘들의 합이 0이라는 점 외에 뭔가 다른 조건이 필요하다.

물체가 평형을 이룬다는 것은 물체에 작용하는 힘의 합력이 0이라는 것 외에 물체에 작용하는 힘이 그 물체의 회전에 미치는 영향, 즉 돌림힘(토크)이 0이 돼야 한다는 조건이 있어야 한다. 그렇다면 돌림힘이란 무엇인가.

말 그대로 물체가 회전할 때 작용하는 힘이다. 생활 주변에서 돌림힘을 이용하는 일들은 비일비재하다. 문을 열 때, 음료 캔을 딸 때, 수돗물을 틀 때 등이 돌림힘이 작용하는 예다. 그런데 문의 측면으로 문을 잡아당기거나 밀면 문은 열리지 않는다. 돌림힘이 작용하려면 문과 수직으로 잡아당기거나 밀어야 한다. 그 이유는 물체의 회전축에서 힘이 작용하는 점까지의 거리의 방향과 힘의 방향이 수직일 때 돌림힘이 작용하기 때문이다. 그래서 돌림힘은 다음과 같이 정의된다.

돌림힘 = 회전축으로부터 작용하는 힘점까지의 거리 × 거리방향과 수직인 힘

장대타기에서 작용하는 돌림힘을 분석해보자. 두팔 중간 거리의 장대부분을 기준으로 돌림힘을 계산해보면, 무게중심점에서의 중력에 의한 돌림힘은 6백30Nm(0.9m×7백N)이고 회전방향은 반시계방향이다. 이때 중력을 상쇄하기 위해 두손에 작용하는 수직방향 각 힘 3백50N에 의한 돌림힘은 0이다. 왜냐하면 힘의 방향과 거리방향이 나란해 거리방향과 수직인 힘이 0이기 때문이다(0 = 0.6m(회전축으로부터 작용하는 힘점까지의 거리)×0N(거리방향과 수직인 힘)).

그렇다면 중력에 의한 돌림힘을 상쇄하기 위해서 두손에 다른 어떤 힘이 작용해야 할까. 그 조건은 중력에 의한 돌림힘과 크기가 같고 회전방향이 반대인 시계방향으로 돌게 하는 힘이다. 이에 따라 아래손에는 몸으로 향하는 힘, 위손에는 몸바깥쪽으로 향하는 힘이 서로 반대이며 크기가 같게 작용해야 한다. 기준점에서 손이 각각 60cm 떨어져있으므로 중력에 의한 돌림힘 6백30Nm를 상쇄하기 위해 두손에 수평방향으로 각각 5백25N(6백30Nm=2×0.6m×5백25N)의 힘이 작용한다.

결과적으로 두손에 작용하는 수직, 수평 방향의 힘을 합성하면 아래손에 작용하는 힘의 방향은 북서쪽, 위손에 작용하는 힘의 방향은 북동쪽이 된다. 따라서 각 손이 장대에 작용하는 방식이 다르다. 각 손에 작용하는 힘의 반대방향으로 손이 장대에 힘을 가하는 것이므로, 아래손은 장대를 밀고, 위손은 장대를 잡아당기는 상황이다.

또한 수평방향의 5백25N과 수직방향의 3백50N을 합하면 6백31N의 힘이 각 손에 작용하는데, 이정도의 힘은 한손은 63kg의 물체를 드는 것이고, 다른 한손은 63kg의 물체를 잡아당기는 셈이다. 정말 대단하지 않는가!

한편 이 묘기에서 다리를 모으고 있다가 벌리는 동작이 있는데, 아마도 보는 이 중에는 ‘다리를 모으고 있는 것도 힘들텐데 벌리기까지 하는구나’라고 생각할 수 있다. 모은 상태와 벌린 상태 중 어느 경우가 더 힘이 많이 필요할까. 이 두 상태의 차이는 무게중심의 위치변화다. 다리를 벌리면 오히려 무게중심이 머리 쪽으로 이동하기 때문에 돌림힘이 줄어든다. 따라서 다리를 벌린 상태가 힘이 더 적게 든다.

탄력비행:번지점프처럼 떨어져 반복회전

번지점프처럼 사람의 등허리쯤에 탄성을 가진 두 줄을 고정시켜 공중을 날아다니는 것처럼 보이는 묘기, 탄력비행. 그러나 번지점프와는 다르다. 신기하게도 내려올 때는 몸이 회전하지 않다가 바닥까지 내려온 다음부터 마구 돌기 때문이다. 여기에는 어떤 비밀이 숨어있는 것일까.

먼저 연기자의 동작을 느린 속도로 자세히 관찰해보자. 연기자는 팔을 머리 위로 쭉 뻗은 상태로 어느 정도 내려오다가 팔을 몸 안쪽으로 모으기 시작한다. 가장 낮은 곳에서 몸은 수평상태가 되고 팔은 허리 옆에 모아져 있다. 다음 몸이 올라가면서 팔을 다시 머리 위로 뻗는 동작을 보여준다. 이때 몸이 반시계방향으로 회전하기 시작한다. 몸이 돌아서 머리가 바닥으로 향하면 다시 팔을 모으기 시작해, 몸이 가장 낮았던 상태와 같아질 때 팔을 최대로 몸에 붙인다. 회전은 계속되고 이와 같은 팔 동작의 변화를 반복한다.

장대타기에서 물체의 회전에 영향을 미치는 돌림힘을 알아보았다. 그렇다면 이 기교에서도 분명 돌림힘이 어디선가 연기자에게 작용한 것이 틀림없다. 그렇다면 그 돌림힘은 어디서 생긴 것일까.

이 기교의 비밀을 풀 중요한 열쇠는 몸에 고정시킨 줄, 그리고 머리 위로 뻗었다가 허리로 모으는 팔의 움직임에 있다. 줄의 한끝은 연기자가 내려오는 곳보다 앞 공중에 고정돼 있고(공중고정점), 다른 한쪽은 연기자의 등허리에 매달아져 있다(몸고정점). 그런데 연기자의 몸에 매달아진 줄의 위치가 매우 중요하다. 그 위치는 바로 팔을 머리 위로 뻗은 상태에서의 무게중심점이다.

처음 수직하강할 때, 연기자에게 작용하는 힘은 중력뿐이다. 그러나 줄이 팽팽해져 늘어나기 시작하면 공중고정점으로 끌어당기는 장력이 발생한다. 따라서 보는 이의 입장에서 연기자의 머리가 오른쪽으로 향하면서, 몸은 진자처럼 타원을 그리는 모양으로 움직이게 된다. 이때 팔을 몸 안쪽으로 모으는 것은 어떤 변화를 주게 될까.

팔을 모으는 동작으로 발생하는 변화는 무게중심점이 다리(몸고정점의 왼쪽) 쪽으로 이동한다는 것이다. 그러면 줄의 몸고정점과 무게중심점이 일치하지 않게 되고 이 때문에 돌림힘이 생긴다. 그리고 가장 낮은 곳에서 팔을 최대로 몸에 붙인 상태는 몸고정점과 무게중심점간의 거리가 가장 커지는 곳이다. 이때 회전하는 돌림힘이 반시계방향으로 최대가 되면서 순간적으로 몸은 회전하기 시작한다.

만약 팔을 계속 머리 위로 뻗은 상태로만 몸을 유지하면 연기자는 어떤 운동을 하게 될까. 무게중심점과 줄의 몸고정점이 일치하기 때문에 돌림힘은 발생하지 않고 단순히 진자와 같은 타원운동을 할 뿐이다.

한편 가장 낮은 상태에서 올라가면서 팔을 다시 머리 위로 뻗는 이유는 반시계방향의 돌림힘을 방해하지 않기 위해서다. 만약 팔을 모으고 돌면 머리가 반대편으로 갔을 때 시계방향으로 돌림힘이 생기기 때문이다. 따라서 팔을 머리 위로 뻗은 상태, 모으는 상태를 머리의 방향에 따라 변화시켜 가면 회전이 계속될 수 있다.

순식간에 흘러가는 동작이라 탄성만 하고 지나갈 뿐, 대부분은 이 뒤에 숨은 이 묘기의 장치와 연기자의 동작간에 이런 상호작용이 있을 것이라고 생각하지 못한다.

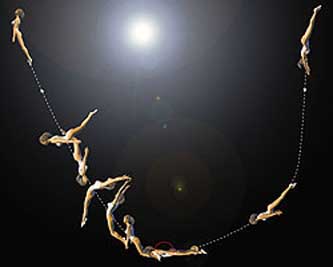
날아다니는 처녀들:몸 펴고 세바퀴 돌기

이번 서울 공연의 피날레를 장식한 공연은 화려한 해외시상 경력을 가지고 있는 ‘날아다니는 처녀들’이다. 현란한 공중곡예 기교를 5분 정도 보여주고 나서 사회자가 다음과 같은 소개를 한다.

“공중에서 세계적으로 가장 높은 기교 동작들을 보시겠습니다.”

공중의 한쪽에서 여자가 아래에 있는 남자의 손을 잡고 기둥을 한바퀴 돈 다음 손을 놓고 공중에서 회전하는 기교를 보여준 후 가운데에서 그네타기를 하고 있는 남자와 만나는 묘기다. 이들 중에서 ‘세바퀴돌기’, ‘몸을 펴고 세바퀴 돌기’가 필자에게 흥미를 끌었다.

‘세바퀴돌기’는 여자가 공중에서 다리를 끌어안고 세바퀴를 도는 것이고, ‘몸을 펴고 세바퀴 돌기’는 말 그대로 몸을 오그리지 않고 편 채 세바퀴를 도는 것이다. 그런데 사회자가 ‘몸을 펴고 세바퀴 돌기’를 ‘세계 최첨단기교’라고 특별히 강조하면서 소개를 하는데 그 이유는 무엇일까.

가령 질량이 같은데, 하나는 럭비공처럼, 다른 하나는 역기처럼 생긴 두 물체가 앞에 놓였다고 하자. 이 두 물체를 회전시키려고 하는데, 어느 것이 돌리기가 쉬울까. 답은 럭비공처럼 생긴 물체다.

물체마다 그 생김새에 따라 회전시키기가 쉬운 것이 있고, 그렇지 않은 것이 있다. 이유는 회전관성 때문이다. 회전관성은 ‘어떤 축에 대해 회전하고 있는 물체는 그 축에 대해 계속 회전하려고 한다’는 성질로, 반면 회전하지 않은 물체에 대해서는 계속 회전하지 않는 상태를 유지하려는 것이다. 그런데 회전관성은 질량에 따라 변하기도 하지만 물체의 질량분포가 회전축으로부터 얼마나 떨어져있느냐에 따라 값이 달라진다. 즉 회전축을 중심으로 물체가 뭉쳐져 있을수록 회전관성은 작아진다.

간단하게 이 사실을 확인해볼 수 있다. 어깨와 나란하게 양팔을 길게 뻗은 상태로 박수를 쳐보자. 다음에는 앞 상태에서 팔꿈치만 90도로 꺾어서 박수를 쳐보자. 금방 어떤 경우가 쉬운지 느낄 수 있다. 두 경우 팔의 질량에는 변화가 없지만 후자의 경우 팔꿈치 아랫부분이 회전 중심과 좀더 가까워 회전관성이 작다.

공중에서 다리를 올려 두팔로 감싸 안고 고개를 숙이면 질량 중심으로부터의 거리는 전체적으로 줄어들어 회전관성도 작아지게 돼 정지한 상태에서 몸을 회전시키기 쉬워진다. 따라서 같은 거리를 회전하는 경우, 몸을 오그리고 도는 것이 몸을 펴고 도는 것보다 쉬운 것이다. 바로 이점이 같은 세바퀴를 도는 것이라도 몸을 펴고 회전하는 것이 세계 최첨단이라고 소개한 이유다.

이처럼 과학적 원리가 숨어있는 묘기를 보여주는 평양교예단은 이 원리를 몸소 체험하는 사람들이다. 여기에서 소개한 것 외에도 평양교예단이 보여주는 묘기들 속에 숨어있는 움직임의 원리를 찾아보는 것은 어떨까. 이를 통해 새로운 묘기를 개발해볼 수 있을지도 모른다.

​