d라이브러리

기온이 낮은데다 바람까지 불면 사람들은 더 추위를 느낀다. 이를 표현한 것이 체감온도. 여름철 기온과 습도가 높을 때 자주 언급되는 불쾌지수와 더불어 겨울철에 등장하는 체감온도가 어떻게 만들어지는지 알아보자.

수학은 기호의 학문이라는 말이 있다. 숫자(0,1,2,···,9)와 미지수를 나타내는 문자(x,y,z,···), 그리고 기지수를 나타내는 문자(a,b,c,···),여기에 이것들을 연결하는 기호(+,-,x,÷,=,<;,>;,···)들이 있으니 말이다. 또 특수한 용도로 이용되는 수많은 기호도 빠뜨릴 수 없다(예를 들어 △,□,{},∈,⊂,Ø,∩,∪,√,${}^{3}$$\sqrt{}$,∞,lim,∑,∫,π,e,···).

수학의 문장은 이런 기호들을 결합시킨 ‘식’으로 표현된다. 그래서 수학은 자연 언어와 매우 다른 특별한 언어다. 이런 언어를 배우기 위해서는 많은 노력과 긴 시간이 필요하다. 분명히 수학은 많은 사람들의 불만과 원성을 들을 만하고, 두려움과 공포의 대상이 되기에 충분하다.

그렇지만 이런 기호 때문에 수학은 일상 언어로 표현하면 매우 길고 모호할 수 있는 내용을 매우 간단한 형태로 명백하고 정확하게 나타낼 수 있다. 수학 이외의 다른 분야에서 발견된 결과와 법칙들을 수학적인 식으로 표현하는 이유가 바로 여기 있다. 수학은 ‘과학의 언어’라는 말도 있지 않은가.

일상 생활에서 자주 접할 수 있는 많은 수치 계산에도 수학적인 식이 이용된다. 그 중 겨울철 자주 접할 수 있는 것으로 체감온도가 있다. 체감온도는 기온, 풍속, 습도 등에 따라 신체가 느끼는 온도다.

바람이 세찰수록 낮아지는 체감온도

겨울철에는 바람 때문에 더욱 춥게 느껴지는 경우가 많다. 같은 온도에서도 바람이 세차게 불수록 체감온도가 낮아지기 때문이다. 풍속을 고려해서 체감온도를 구하는 한 가지 방법을 알아보자. 온도가 t (℃)이고 풍속이 v (m/초)일 때 체감 온도 T (℃)를 구할 수 있다. 이때 T 를 풍랭 지수(wind-chill index)라고 하는데 구하는 식은 다음과 같다(표).

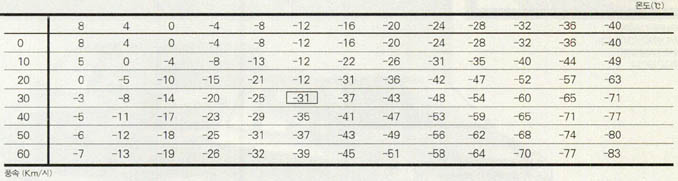
T = 33- $\frac{1}{22.04}$ (10.45 + 10$\sqrt{v}$-v)(33-t)

이 공식은 풍속이 초속 1.79m(빠르게 걷는 속도)와 초속 20 m(시속 72km) 사이일 때 사용되며, 피부의 온도를 33 ℃로 가정하고 있다. 예를 들면 온도가 0 ℃이고 풍속이 초속 5 m(시속18km), 초속 10 m(시속 36 km), 초속 15 m(시속 54km)일 때의 체감 온도는 각각 -8.6℃, -15℃, -18℃이다.

한겨울에 기온이 영하 12 ℃이고 풍속이 시속 30 km이면 이때의 체감온도는 약 영하 31 ℃가 된다. 겨울 바람을 매섭게 느끼는 이유가 여기에 있다.

온도와 습도로 구하는 불쾌지수

체감 온도가 주로 겨울에 사용된다면 여름철에 자주 등장하는 용어는 불쾌지수(discomfort index)다. 불쾌지수 D 는 건습구 습도계에서 건구 온도(통상적인 온도) d ℉와 습구 온도 w ℉를 다음과 같은 공식으로 구한 화씨 온도로 D = 15 + 0.4(d + w) 식으로 주어진다. 이때 화씨 온도 F 와 섭씨 온도 C 사이의 관계는 F = $\frac{9}{5}$ C + 32이다. 불쾌 지수가 70 이하일 때, 즉 식에서 구한 화씨 온도가 70 ℉ 이하일 때, 대부분의 사람들은 매우 쾌적하게 느낀다. 그리고 70 이상이면 약 10%, 75 이상이면 약 50%, 80 이상이면 대부분의 사람이 불쾌감을 느낀다고 한다.

미국에서는 불쾌지수를 발표함으로써 불쾌감을 더욱 조장한다고 해서, 이를 온습 지수(temperature-humidity index, THI)라는 말로 바꾸었다. 우리가 일상적으로 사용하는 섭씨 온도를 기준으로 보면 건구 온도가 a ℃이고 습구 온도가 b ℃일 때, 불쾌 지수 D는 D = 40.6 + 0.72(a + b)로 나타난다. 요즘과 같이 건조할 때 건구 온도가 18℃이고 습구 온도가 15℃일 때 불쾌지수는 약 64정도로 여름에 느낄 수 있는 불쾌감은 찾아보기 힘들다. 오히려너무 건조해 정전기가 자주 발생하므로 여름과는 다른 형태의 괴로움을 느낀다.