d라이브러리

'알고 보면 과학' 인 것은 우리의 일상에 너무 많이 숨어있다. 스포츠에 사용되는 공 가운데 유일하게 오목오목 곰보형인 골프공. 왜 곰보가 됐어야만 했는지 알아보자.

사람들은 동그란 모양의 공을 가지고 여러 가지 운동경기를 한다. 운동경기마다 공의 크기는 제각각이지만 공통점은 표면이 매끄럽다는 것이다. 그런데 유난히 골프공만 표면이 곰보이다.

왜 골프공만 표면이 곰보처럼 오목하게 패인 것일까. 골프공을 본 사람이면 누구나 다 가지는 의문이다. 골프공의 표면이 거친 이유는 공을 멀리 날아가게 하기 위해서다. 거친 표면의 공이 매끄러운 표면의 공보다 멀리 날아간다? 믿기 힘든 이야기다.

골프공도 처음에는 다른 공들과 마찬가지로 표면을 매끄럽게 만들었다. 새로 산 매끄러운 공을 자꾸 치다 보면 공이 닳게 되고 표면이 거칠게 변했다. 사람들은 오래 되어 표면이 거칠어진 공이 매끈한 새 공보다 멀리 날아간다는 사실을 알게 됐다. 그렇게 해서 지금의 골프공이 탄생했다.

골프공뿐 아니라 모든 공이 무한정 날아가지 못하는 것은 공기의 저항을 받기 때문이다. 공기가 없는 달에서는 지구에서와 같은 힘으로 골프공을 칠 경우 지구에서보다 더 멀리 날아갈 것이다.

공기 저항에는 두 가지 종류가 있다. 첫번째는 공의 앞 뒤 표면에 작용하는 압력의 차이 때문에 생기게 되는 저항이다(형상저항). 이 저항은 물체의 형상에 의해 결정된다. 두번째는 공기와 공의 마찰로 인해 발생하는 마찰저항이다.

공의 경우 형상저항이 전체저항의 대부분을 차지한다. 그래서 공을 멀리 날아가게 하려면, 형상저항을 감소시켜야 한다. 골프공의 표면이 울퉁불퉁한 것은 형상저항을 감소시키기 위한 것이다.
 

유체역학의 아버지, 레이놀즈

공기저항을 줄이기 위해 왜 공의 표면이 울퉁불퉁해야 할까. 이를 이해하려면, 난류(turbulence, 亂流)를 알아야한다. 난류는 우리가 초등학교부터 배우던 난류(따뜻한 바다의 흐름)와 한류(차가운 바다의 흐름)의 그 난류가 아니다.

기체 또는 액체(이를 통틀어 유체라고 부른다)가 어느 정도 이상의 속도를 가지고 흐르게 되면 유체는 매우 복잡한 현상을 보인다. 이것을 난류라고 한다.

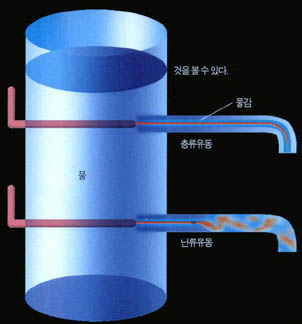
수도꼭지를 천천히 틀어 보면, 물이 수도꼭지에서 부드럽게 흐른다(층류유동, larminar flow). 조금 더 틀게 되면 수도꼭지에서 나오는 물은 매우 불규칙하게 흐르게 된다(난류유동, turbulent flow). 수도꼭지의 물 흐름을 가만히 지켜보면 한번도 같은 형태의 물줄기를 찾아볼 수 없을 것이다. 만약 한번이라도 같은 형태의 물줄기가 발견된다면, 그것은 난류유동이 아니라 층류유동이다.

우리가 보고 다니는 또는 느끼는 유체의 흐름은 대부분 난류유동이다. 자전거나 자동차 또는 배를 타고 갈 때 주위에 흐르는 공기나 물의 흐름은 모두 난류라고 보면 된다. 겨울철에 벽에서 나오는 스팀으로 방안의 공기가 따뜻해지는 것도 바로 스팀이 난류유동이기 때문이다. 만약 스팀이 층류유동이라면 방안의 공기를 데우는데만 며칠이 걸릴 것이다.

유체의 흐름을 과학적으로 규명하고자 하는 노력은 아주 오래 전부터 이뤄졌다. 층류와 난류 구분에 대한 실험은 1883년 레이놀즈에 의해 행해졌다(그림1). 그는 파이프를 흐르는 물에 물감을 투입해 층류유동과 난류유동을 분명히 보여주었고, 두 흐름을 구분짓는 변수가 무엇인가를 명확하게 제시했다. 그 변수는 그의 업적을 기리어 레이놀즈 수(Reynolds number)라고 불린다. 레이놀즈 수는 유체유동을 공부하는 데에 있어서 가장 중요한 변수이다.
 

공기를 부드럽게 흐르게 하려면

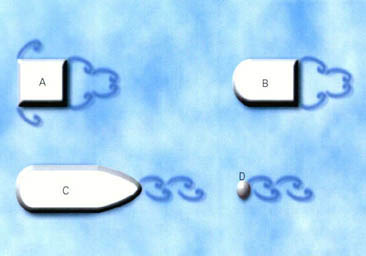
다시 골프공으로 돌아가자. 형상저항을 줄이기 위해서는 공기가 공의 표면을 부드럽게 따라 흘러야 한다. 그러나 속도가 커지게 되면 공기가 공의 표면을 따라 부드럽게 흐르지 못하고, 공의 중간쯤에서 공기의 흐름이 공의 표면에서 멀어진다(그림2, 왼쪽). 이때 공의 중간 이후부터 공기의 속도가 급격하게 떨어짐과 동시에 공기 흐름의 방향이 바뀐다.

이렇게 뭉툭한 물체의 뒤에서 공기의 흐름이 바뀌면 그 곳의 압력이 뚝 떨어지게 된다. 그래서 공의 앞면에서는 높은 압력이, 뒷면에서는 낮은 압력이 걸려 큰 형상저항이 발생하게 되고, 이로 인하여 공은 멀리 날아가지 못하게 되는 것이다.

그런데 공의 표면을 약간 울퉁불퉁하게 만들면, 공의 앞 표면에서 난류유동이 발생하게 된다. 난류유동이 발생하면 유체의 섞임이 활발하게 돼 공기의 흐름이 바뀌는 현상이 공의 뒷면에서만 일어나게 된다(그림2, 오른쪽). 이렇게 되면 낮은 압력을 가지게 되는 공의 표면이 줄어들게 돼 공의 형상저항이 감소하게 되는 것이다. 이 원리를 이용한 것이 골프공이다.

지금의 골프 공 표면을 매끈하게 만들면 날아가는 거리는 얼마나 줄어들까? 놀랍게도 날아가는 거리는 대략 반으로 준다. 공의 표면에 작은 돌기를 줌으로써 골프 공은 두 배를 날아갈 수 있는 것이다.

그렇다면 날아가는 모든 물체의 표면에 작은 돌기를 주어 공기 저항을 감소시킬 수 있지 않을까. 예를 들어 총알의 표면에 돌기를 주면 더 멀리 날아가게 할 수 있지 않을까. 애석하게도 돌기를 만들어도 물체의 크기와 속도에 따라 저항이 감소하는 것이 있고 그렇지 않은 것이 있다. 그 가능성 여부를 판단하는 것이 바로 레이놀즈 수이다.

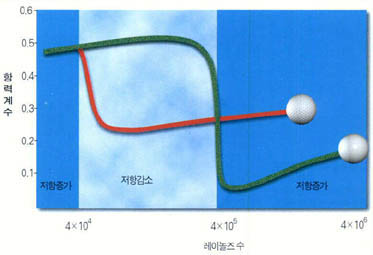
레이놀즈 수에 따라 유체의 흐름은 층류유동과 난류유동으로 구분된다. 물체의 표면에 돌기를 주어 형상저항을 감소시키는 레이놀즈 수는 약 4만에서 40만 정도이다(그림3). 이 범위보다 레이놀즈 수가 커지거나 작게 되면 오히려 전체저항이 커지게 된다.

골프공이 날아갈 때의 레이놀즈 수는 약 5만에서 15만정도이므로 돌기를 만들어 형상저항을 줄일 수 있다. 탁구공의 레이놀즈 수는 4만보다 작기 때문에 탁구공의 표면은 일부러 매끄럽게 만든다. 시속 1백50km의 속도를 자랑하는 선동렬 선수의 야구공은 어떨까. 이 때의 레이놀즈 수는 30만 정도이다. 이정도 또는 이보다 느린 속도의 야구공은 실밥이 저항을 줄이는데 큰 역할을 할 수 있다. 실밥에 의한 유동이 난류유동이 돼 형상저항을 덜 받기 때문이다.
 

상어비늘의 비밀

고속으로 날아가는 물체의 모양을 결정하는 데에 빼놓을 수 없는 것이 형상저항의 감소다. 이 저항을 줄이기 위해 필수적인 것이 유선형의 몸매이다. (그림4)는 물체의 형상을 유선형으로 바꿈으로써 공기저항이 얼마나 줄어들 수 있는 지를 보여준다. 직사각형이 일정한 속도로 날아갈 때의 저항을 1이라 하자. 직사각형의 앞쪽을 둥글게 해 유선형으로 만들어 주면 저항은 0.5정도로 줄어든다. 직사각형의 뒤쪽을 유선형으로 만들어 주면 저항은 0.08 정도가 된다. 같은 연료를 사용할 때 유선형으로 만든 차가 직사각형으로 만든 차에 비해 연료를 13배 줄이게 된다는 뜻이다. 하늘을 나는 새들이나 물 속을 자유로이 움직이는 물고기의 형상이 유선형인 것은 바로 이 형상저항을 줄이기 위해서다.

물체를 충분히 유선형으로 만들었을 경우, 그 다음에 감소시켜야 하는 저항은 마찰저항이다. 자연에서 진화에 의해 마찰저항을 줄이도록 몸체 표면을 변형시킨 대표적인 예가 바로 상어다.

상어의 표면을 살펴보면, 상어비늘에 미세한 작은 갈비뼈 모양의 돌기(리블렛, riblet)가 있음을 볼 수 있다. 왜 상어 비늘에 이와 같은 돌기가 있을까. 독일의 생물학자들과 기계공학자들의 공동연구에 의해 이것이 마찰저항과 밀접한 관련이 있음이 밝혀졌다. 그후 1980년 미항공우주국(NASA) 랭글리(Langley) 연구소에서 이 현상을 연구하기 위해 상어비늘 형상을 여러 가지로 실험한 결과, 이 비늘은 난류유동에서 마찰저항을 줄이는 효과가 있음을 발견했다. 이 상어 비늘 모양을 벽면에 부착할 경우 최대 8%까지 마찰저항을 줄일 수 있음을 보고했다.

유럽의 비행기 제조회사인 에어버스(Airbus)사에서는 이 리블렛을 비행기 날개 및 동체에 부착해 약 2%의 저항을 줄이는 데에 성공했다. 리블렛은 요트, 수영복 등에 부착돼 마찰저항을 줄이는 중요한 도구로 쓰이고 있다.

왜 리블렛이 마찰저항을 줄이는가에 대해서는 최근까지 그 이유가 규명되지 못했으나, 1992년 필자가 미국 스탠포드 대학에서 슈퍼 컴퓨터 크레이(CRAY)를 사용해 이를 밝혔다. 리블렛에 의해 난류유동이 형성되어 있을 때, 마찰저항을 일으키는 가장 큰 주범은 보텍스이다.
보텍스(vortex)는 유체가 회전하는 모양인데, 벽 가까이 보텍스가 존재하면 마찰항력이 크게 증가한다. 그런데 리블렛은 보텍스를 벽에서 멀리 떨어지게 함으로써 마찰저항을 감소시키는 것이다. 상어비늘의 리블렛 간격은 약 0.1mm 이고, 비행기에 사용되는 리블렛의 간격은 수십μ 으로 매우 작다.
 

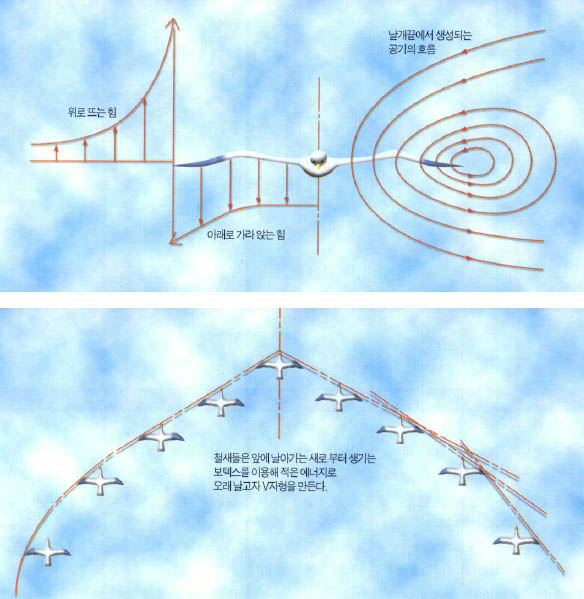
철새가 V자로 날아가는 이유

자연에서 보텍스를 이용한 재미있는 예가 있다. 철새들은 V자로 대열을 만들어 날아간다. 왜 철새들은 일렬로 날아가지 않을까. 철새가 V자를 그리는 이유는 양력(위로 뜨는 힘)을 받기 위해서다. 먼 거리를 날아가는 철새들에게는 에너지를 줄이기 위해 작은 날개짓으로 공중에 떠 있는 것이 무엇보다 중요하다. 맨 앞에서 날개짓하는 철새에 의해 공기 중에 보텍스가 형성된다(그림5). 이 보텍스는 철새 날개 바깥쪽 부근에서 공기의 흐름을 위로 올라가게 한다. 그러면 공기가 위로 올라가는 위치에 있는 뒤쪽의 철새는 보다 작은 날개짓으로 하늘에 떠 있을 수 있다. 같은 방식으로 그 다음에 있는 철새도 앞에 날아가는 철새의 바깥쪽에 위치한다. 그래서 전체적으로 V자를 그리게 된다. 철새들은 긴 거리를 나는 동안 힘이 덜 드는 배열을 파악해 날고 있는 것이다.

비행기가 착륙을 할 때도 비행기 날개에 의해 이와 유사한 형태의 보텍스가 생긴다. 이 보텍스는 매우 강한 크기인데 비행기가 착륙한 이후에도 얼마동안 남아있게 된다. 뒤이어 착륙하는 비행기가 우연히 앞 비행기의 보텍스 중심을 뚫고 지나가게 되면, 한 쪽에서는 위로 뜨는 힘을 다른 한 쪽에서는 아래로 가라앉는 힘을 받게 돼 비행기가 전복될 수 있다. 그래서 모든 비행장에서는 보텍스에 의한 불의의 사고를 대비하기 위해 비행기들의 착륙에 시간차를 두고 있다.

난류유동은 우리가 살고 있는 모든 곳에 존재한다고 해도 과언이 아니다. 난류는 그 불규칙성과 비선형성으로 인해 매우 어려운 학문 분야로 알려져 있다. 노벨 물리학상 수상자인 파이만(R. Feyman)교수는 난류를 “고전물리에서 풀리지 않은 가장 중요한 문제”라고 언급했다. 과학이 발달할수록 모든 운송체의 속도는 빨라지고 있다. 그래서 난류유동 해석은 더욱 중요해지고 있다.