이제 진정 '페르마의 정리'가 증명된 것일까. 지난 93년 와일츠 교수의 발표 이후 온갖 화제로 들끓었던 수학계의 흥분은 아마도 코언의 새로운 논문 발표로 일단 막을 내린 것 같이 보인다.
지난해 10월28일자동아일보에 '수학계 3백년 난제 풀릴 듯'이라는 제목의 기사가 실렸다. 지난 93년 6월23일 미국 프린스턴 대학의 A.와일츠 교수가 성공했다고 단언한 3백50년 전의 '페르마의 정리'의 증명이다. 하지만 와일츠의 증명에도 잘못이 있었다. 이번에는 그 미비한 점을 보완한 완전한 증명이라는 주장이다.
또 하나의 실패
와일츠 교수가 그것을 발표했을 당시 전 세계의 수학자들은 놀랐다. 그간 그 증명에 필요한 예비정리가 발표됐고 또한 와일츠 교수의 실력으로 보아 누구나 그의 성공을 의심하지 않았다. 하지만 그의 논문 내용은 너무 난해하고 좀처럼 진부를 가릴 수 없었다.
그 후 와일츠의 논문에서 결점이 발견됐다. 이번에는 와일츠와 같은 대학에 있는 S.코언 교수가 완벽하게 논문을 만들어냈다고 발표 한 것이다.
저명한수학자 E.T.벨(1883-1960)은 다음과 같은 글을 남겼다.
"여러분이 혹시 이 문제의 증명에 성공했다고 생각하더라도 그것을 나에게 보내주지 말기를 바랍니다. 나는 지금까지 증명에 성공했다는 1백편 정도의 논문을 읽었습니다. 제발 이 문제로 나를 이 이상 괴롭히지 말아주십시오. 나는 얼마 전 어떤 논문의 증명이 잘못 돼 있다는 것을 3주 이상 걸려 찾아냈습니다. 나의 강의를 듣는 여학생이 30분정도 읽다가 그 잘못을 발견해냈습니다. 이 문제에 도전하고자 하는 사람에게는 20세기 최대의 수학자의 한 사람인 힐버트(D.Helbert)가 '왜 이 문제를 해결하려 하지 않는가'라는 질문을 받고 다음과 같이 대답한 것이 참고가 될 것입니다. 그것은 '처음 3년간 준비를 위한 공부를 열심히 해야 하지만 결국 실패할 가능성이 높고, 또 나는 그만큼 시간을 낭비할 여유 있는 사람이 아니다'라는 말입니다."
문제의 발생
페르마(Fermat)는 정식으로 논문을 발표하는 일이 거의 없었다. 다른 수학자들과 편지를 통해 겨우 수학에 관한 정보만을 교환할 정도였다. 그는 자기가 풀었다고 생각하는 문제를 그가 애독한 디오판토스의 '수론' 필사본의 여백에 썼다. 그내용을 오늘날의 형식으로 바꿔쓰면 다음과 같다.
"n>;2인 정수에 대해서 ${a}^{n}$=${b}^{n}$+${c}^{n}$의 관계를 만족하는 정수 a, b, c는 존재하지 않는다. 나는 이 정리에 관해 훌륭한 증명을 해낼 수 있었다. 하지만 여백이 적어서 그것을 적을 수 없다"
이 짧은 글이 소위 페르마의 대정리의 내용이다. 페르마의 증명 내용은 알 수 없다. 아마도 그의 성공은 착각이었던 것 같다. 그 후 수 많은 수학자가 도전했으나 지금까지 성공한 사람은 없었다.
A.D.3세기경 디오판토스(Diophantos)는 고대 그리스의 대수학을 완성시켰다. 그의 '수론'은 유클리드의 기하학에 맞서 고대 그리스의 대수학을 대표한다. 특히 그는 a, b, c가 정수 일 때 ${a}^{2}$+${b}^{2}$+${c}^{2}$, 즉 피타고라스의 정리와 관련된 문제를 연구했다. 페르마는 이 책에서 크게 자극을 받은 것이다.
페르마는 유복한 상인의 아들로 태어나 처음에는 법률 공부를 했다. 그는 수학에 취미를 갖기 시작하고 독학으로 공부해 당시 최고의 수준에 도달, 정수론의 기초를 마련했다. 그의 중요한 업적에는 17=${4}^{2}$+${1}^{2}$, 137=${11}^{2}$+${4}^{2}$과 같이 4n+1 모양의 소수는 모두 두 개 정수의 제곱의 합으로 나타낼 수 있다는 것이다. 소수는 2,3,5,7… 과 같이 1과 자기 자신 이외의 약수를 갖지 않는 수다.
17=4·4+1, 137=4·34+1
그 외에도 그의 중요한 증명은 모두가 그의 친구와의 편지에 밝혀져 있으며, 페르마는 단순한 상상이 아니라 거기에서 다음과 같은 강하법이라는 특수한 증명법을 고안해냈다.
"4n+1의 모양을 갖는 소수로서 제곱의 합이 아닌 것이 있을 때는 그보다 작은 4n+1의 모양을 한 소수로서 제곱의 합이 될 수 없는 것이 있다."
이 작업을 계속 진행하다 보면 결국 4n+1의 모양을 한 소수 5(5=4·1+1)도 두 제곱수의 합이 될 수 없다는 것이다. 하지만
5=${2}^{2}$+${1}^{2}$이므로 모순이 된다. 오늘날 수학에서는 이것을 귀납법이라고 한다.
페르마는 디오판토스의 제곱수를 두 개의 제곱수로 나타내는 문제에서 3제곱, 4제곱의 경우를 생각했고 드디어 일반적으로 ${a}^{n}$=${b}^{2}$+${c}^{n}$, (n>2)의 경우를 생각했을 것이다. 그 후 저명한 수학자들 모두가 이 문제에 관해서 손을 댔다.
오일러 (L.Euler, 1707-1783)는 n=3의 경우를 증명했고, n=5에 대해서는 1828년 디리클레(P.G.L.Dirichlet, 1805-1859), 르장드르(A.M.Legendre, 1752-1833)가 증명했다. 그 후 디리클레는 n=14의 경우를 증명했다. 그것은 이상하게 n=7의 경우보다 쉬웠다.

대수적 수
이 문제는 단순히 보통 수만을 주목해서는 소용이 없었음이 일찍부터 알려져 있다. 새로운 '대수적인 수'라는 개념이 필요했다. 대수적인 수란 ${a}_{0}$+${a}_{1}$x+……${a}_{n}$${x}^{n}$=0(${a}_{n}$는 유리수)의 근이 되는 수다. 가령 $\sqrt{2}$는 ${x}^{2}$—2=0의 근이므로 대수적 수이며 π는 대수적 수인 수가 아닌 초월수다.
페르마는 ${y}^{2}$+2=${x}^{3}$의 정수해는 y=±5, x=3에 한한다고 주장했다.
(${5}^{2}$+2=${3}^{3}$ 즉 25+2=27)
이것은 a+b$\sqrt{-2}$와 같은 형태를 지닌 대수적 수를 이용해서 증명할 수 있었다. 이 방정식은
(y+$\sqrt{-2}$)(y-$\sqrt{-2}$)=${x}^{3}$
으로 쓸 수 있는데, 좌변의 두 인수 사이에는 공통 인수가 없다.
정수의 경우 서로소인 두 개의 수의 곱이 3제곱수이면 이들이 각각 3제곱수로 돼 있으나 그것이 a+b$\sqrt{-2}$의 수에 대해서 성립하면 a,b에서
y+$\sqrt{-2}$=${(a+b\sqrt{2})} ^{3}$
양변의 $\sqrt{-2}$의 계수를 비교해서
1=b(${3a}^{2}$-${2b}^{2}$)
여기서 b=±1, ${3a}^{2}$-${2b}^{2}$=±1, 또한 a=±1, b=1
여기서 x=3, y=±5를 얻는다. 수의 세계가 복소수로 확장됨으로써 그보다 적은 범위의 정수세계의 문제가 잘 보이게 된 것이다.
원분수
그 후 수학은 계속 발전해 1의 복소수 근, 가령 ${x}^{3}$—1=(x—1)(${x}^{2}$+x+1)에서 1의 3제곱근(${x}^{3}$=1)은 x=1, $\frac{-1+\sqrt{3}i}{2}$,
성급한 수학자는 이것으로 페르마의 정리가 증명됐다고 발표했다. 하지만 원분수를 이용하는 데에도 한계가 있다. 즉 n=23일 때 분해가 한 가지 방법(일의적)으로는 성립될 수 없음이 밝혀진 것이다.
방정식의 구멍
수학은 계속 발전하며 대수기하의 분야가 개척됐다. 현재 정수론에서 눈부시게 발전하고 있는 분야는 대수와, 도형의 성질을 이용하는 학문인 기하의 경계분야. 대수기하는 방정식으로 정의된 도형의 성질을 연구하는 수학이다.
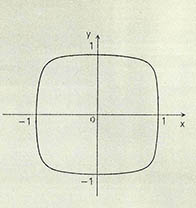
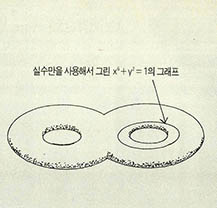
가령 ${x}^{2}$+${y}^{2}$=1로 정의된 도형을 생각해 보자(그림 1). 대수기하에서는 x, y를 복소수로 생각해 x축 y축을 복소평면으로 한다. 이때 각축이 2차원이므로 도형은 현실의 3차원 공간 속에서는 그릴 수 없고, 4차원 속에 그려지는 곡선이 된다. 실수만으로 된 도형 ${x}^{6}$+${y}^{2}$의 그래프는 이 표면상에 있는 닫혀진 곡선이 된다(그림 2).
이와 같은 방정식으로 정의되는 도형의 모습은 미묘하다. 이 사실은 19세기 중엽 리만에 의해 발견됐다. 이 곡면을 ${x}^{6}$+${y}^{2}$=1의 리만면이라 한다. 특히 x+y=1의 경우 x, y를 실수로 해서 그래프를 그리면 1차원의 도형(곡선)이 되고, 복소수로서 그래프를 그리면 2차원의 곡선이 된다. 또한 가령 ${x}^{6}$+${y}^{7}$+${z}^{11}$+${u}^{2}$=1에서 x, y, z, u를 실수로 한 그래프를 그리면 3차원의 도형, 복소수이면 6차원의 도형이 된다.
리만면을 비롯해 이와 같은 고차원의 도형을 연구하는 것이 대수기하학이다. 가령 n≥1을 자연수로 하고 ${x}^{n}$+${y}^{2}$=1 을 복소수로 그리면 몇개의 구멍이 있는 도넛의 표면이 되고, 구멍의 개수는 n이 짝수이면 $\frac{n-2}{2}$개다.
${x}^{8}$+${y}^{2}$=1은 구멍이 $\frac{8-2}{2}$=3개, ${x}^{2}$+${y}^{2}$=1은 구멍이 $\frac{2-2}{2}$=0개, 즉 구의 표면이다. x, y에 관한 방정식, 가령 ${x}^{6}$+${y}^{2}$=1 또는 ${x}^{3}$+${y}^{5}$=6xy+1의 리만면, 즉 복소수를 사용한 그래프 구멍의 수(種數)가 2개 이상이면 유리수의 해는 유한개, ${x}^{6}$+${y}^{2}$=1의 종수가 2이며, ${x}^{2}$+${y}^{2}$=1을 만족하는 유리수의 해는 (0, ±1) (±1,0)의 2개뿐이다.
요컨대 복소수로 그래프를 그렸을 때의 도넛 구멍의 수, 즉 대수기하학의 대상과 유리수의 해가 어떤 관계에 있는가라는 정수론적 성질의 관계를 알리기 시작한 것이다. 정수론과 대수기하학의 경계점이란 바로 이것을 말한다. ${x}^{n}$+${y}^{n}$=1은 n≥3이면 유리수의 해(x, y), x≠0, y≠0가 없다는 것은 이와 같은 정수론과 대수기하학의 경계분야에 있는 것이다.
방정식에 관해 그 정수의 해, 유리수의 해를 논하는 일은 소박하고 고전적인 정수론의 문제다. 하지만 실제 그것은 단순한 식의 변형과 같은 초등적인 방법으로는 도저히 들어갈 수 없는 어려운 문제다. 현대 수학은 그와 같은 소박하고 고전적인 정수론의 문제에 본질적으로 대응할 수 있는 고도의 단계에 도달한 것이다.
최후의 단계
수년 전 독일의 무명 수학자였던 당시 24살의 휠칭스라는 젊은이가 내놓은 이론이 있다. 고전적 정수론에서 근대적 정수론(또는 대수적 정수론)을 생각하고 여기에 새로운 기하학적 수법을 가미했다. 기하학적 정수론이라고 할까, 대수기하라고 할까.
즉 '페르마 방정식은 각 n에 대해서 만일 해가 존재한다 해도 유한개만이 존재한다'는 것이다. 전세계의 수학자들을 놀라게 한 것은 그 증명법이 기하학적이었고 또한 넓은 응용범위를 갖는다는 것이었다. 페르마 방정식의 양변, 즉 ${x}^{n}$+${y}^{n}$=${z}^{n}$을 ${z}^{n}$으로 나누면 ${x}^{n}$+${y}^{n}$=1의 형이 되고 그것은 x, y평면상의 곡선이다(n=2이면 원).
'어떤 곡선상에 좌표가 유리수인 점은 유한 개밖에 없음'을 증명한 휠칭스는 위에서 말한 정리의 결과에 도달했다. 이제는 유한개만 존재한다는 결과를 연장해서 0개만 존재한다고 증명하면 되는 것이다. 와일츠 교수는 이 마지막 단계를 증명한 것 같다.
여기서는 타원함수의 이론이 응용돼 있다. 타원함수란 타원의 호의 길이를 계산할 때 나타내는 함수의 그래프로 ${y}^{2}$=(x의 3차식)과 같은 형식을 취한다. 가령 ${y}^{2}$=${x}^{3}$+1과 같은 것이다.
이처럼 준비된 와일츠의 증명에도 허점이 있었다. 드디어 코언 교수가 그 결점을 보완했다는 것은 단순한 문제가 아니라 새로운 수학적 부산물을 수반한 것이다.
과거 3백50년동안은 온갖 실패와 좌절의 연속이었다. 어느 수학 애호가는 노벨상 이상의 금액에 해당하는 거금을 현상금으로 걸었다. '페르마의 정리를 구하는 데 성공한 사람에게 10만 마르크를 증정하겠음'이라는 구호와 함께.
이제 진정 그 정리가 증명된 것일까. 지난 93년 와일츠 교수의 발표 이후 온갖 화제로 들끓었던 수학계의 흥분은 아마도 코언의 발표로 일단 막을 내린 것 같이 보인다. 이미 그에게 상금의 의미는 없었다. 거듭되는 인플레 때문에 1백년 전의 10만 마르크는 이제 별로 큰 돈이 아닌 것이다. 하지만 그 영광은 그 이상의 것이 될 것이다('과학동아' 1993년 11월호 참조).