d라이브러리

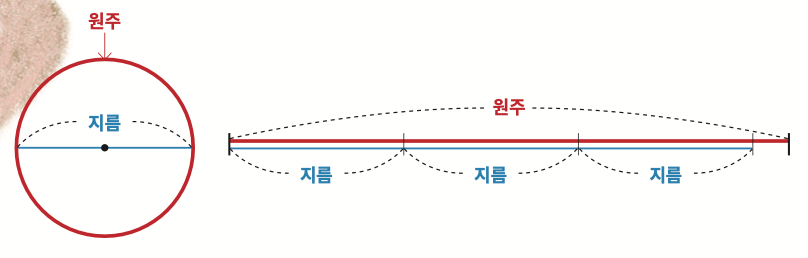
원의 둘레를 조금 어려운 말로는 ‘원주’라고 불러. 원의 지름이 길어질수록 원의 둘레도 길어지지. 뭐, 원이 커지니까 당연한 거 아니냐고?

놀랍게도, 원의 둘레는 아무렇게나 길어지는 게 아니야! 옛날 사람들은 원의 지름과 원의 둘레 사이의 특별한 관계를 밝혀냈어. 바로, 원의 둘레는 언제나 원의 지름보다 약 3배 조금 넘게 길다는 사실이야!

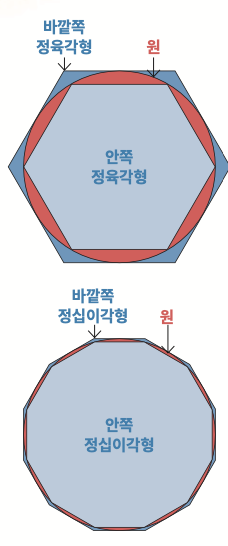
3배 ‘조금 넘게’라니, 애매하다고? 고대 그리스의 수학자 아르키메데스도 원의 둘레가 원의 지름과 비교해 정확히 얼마만큼 길어지는지 알아내고 싶었어. 그는 원 하나를 그린 뒤, 원의 안쪽과 바깥쪽에 원의 둘레와 만나는 정육각형을 하나씩 그렸지. 원의 둘레는 바깥쪽 정육각형의 둘레보다는 조금 작지만, 안쪽 정육각형의 둘레보다는 조금 커. 그다음엔 정십이각형, 정이십사각형, 처럼 각이 더 많은 정다각형을 원의 안쪽과 바깥쪽에 그린다고 생각해 본 거야. 

아르키메데스가 구십육각형까지 계산해 봤더니 원의 둘레는 지름의 약 3.14배였어! 후대의 수학자들은 연구를 거듭했고, 원의 둘레가 지름의 3.14159265358979323846배라는 걸 밝혀냈어. 소수점 아래로는 수가 끝없이 이어진다는 것도 알아냈지. 그래서 이 수를 이용할 땐 3.14로 계산하기로 약속했어. 또, 이를  원주율이라고 부르고  파이(π)라는 기호로 나타내기로 했어. 

나를 둘러싼 흥미로운 이야기, 어때? 나를 꼭 기억해 줘. 나는 ‘원’이야!