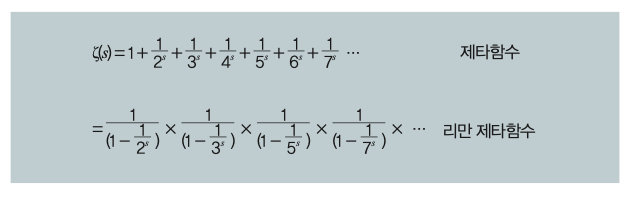페르마는 소수에 관한 추측도 제시했다. 음수가 아닌 정수 n에 대해 22^n + 1꼴의 수는 모두 1과 자신만을 약수로 갖는 소수라는 게 그의 추측이다. 현재는 이런 수를 ‘페르마 수’라 부르며 Fn으로 표기한다.
예를 들어 F0는 3, F1은 5로 명백한 소수다. 비슷한 방법으로 계산해보면 F2 = 17, F3 = 257, 그리고 F4 = 65537로 모두 소수다. 하지만 페르마는 이 추측 또한 증명을 남겨놓지 않았다.

약 100년 뒤인 1732년, 누군가 무덤 속에서 평온하게 잠자고 있던 페르마 수를 끄집어냈다. 오일러다. 그는 F5를 소인수분해 하며 페르마의 추측을 무너뜨린다. F5는 식에 대입해 계산하면 4294967297다. 오일러가 등장하기까지는 아무도 이 수가 소수인지, 합성수인지 밝히지 못했다. 오일러는 이 수가 641과 6700417로 소인수분해 되는 합성수라며, 페르마 수는 모두 소수라는 페르마 추측을 단 한 방에 깨부쉈다.
이후 페르마 수 중 소수라고 밝혀진 건 n이 0, 1, 2, 3, 4일 때뿐이다. n이 5, 6, 7, 8일 때는 완전히 소인수분해 됐다. 하지만 아직 소수인지 합성수인지 알려지지 않은 경우가 더 많다. 그 중 일부는 소인수의 일부만 알려져 합성수인 것으로 확인됐지만, 어떤 소인수로 구성돼 있는지 밝혀지지 않았다.
2024년 현재 324개의 페르마 수가 합성수라는 게 밝혀졌으며 매년 수학자들이 조금씩 더 찾아내 끊임없이 페르마의 추측을 공격하고 있다. 페르마 수에 관한 풀리지 않은 문제도 여전히 있다.

목사를 꿈꿨던 수학자
페르마의 소정리를 증명하고 페르마 수의 반례를 찾아낸 오일러는 페르마의 연구 결과를 발굴하며 그 내용에 매료됐고, 이어 다수의 결과를 증명하고자 노력했다. 이렇게 페르마의 연구 내용은 결과적으로 소수 연구를 한층 더 나아가게 했다.
오일러는 수학 역사상 최고의 천재로 평가받는 수학자다. 그는 평생 발표한 논문이 800편이 넘을 정도로 연구를 많이 했다. 순수 수학과 응용 수학 모두에 정통했고 중요한 의의를 지니는 이론과 개념을 만들었다. 수학을 비롯해 의학식물학화학천문학 등 많은 분야를 연구했다.
메르센과 비슷하게 어렸을 때는 목사가 되고 싶어 스위스 바젤대학교에서 신학을 공부했다. 그러다 과학자, 수학자를 많이 배출한 베르누이 집안 사람들과 만나면서 수학에 눈을 뜬다. 20세인 1727년에 러시아 제국의 페테르부르크 아카데미로 건너가 24년을 머무른다. 1735년에는 시력을 잃었는데도 천부적인 기억력과 강인한 정신력으로 독일과 러시아를 오가며 연구를 이어갔다. 이때도 매주 한 편씩 논문을 작성했다고 전해진다.
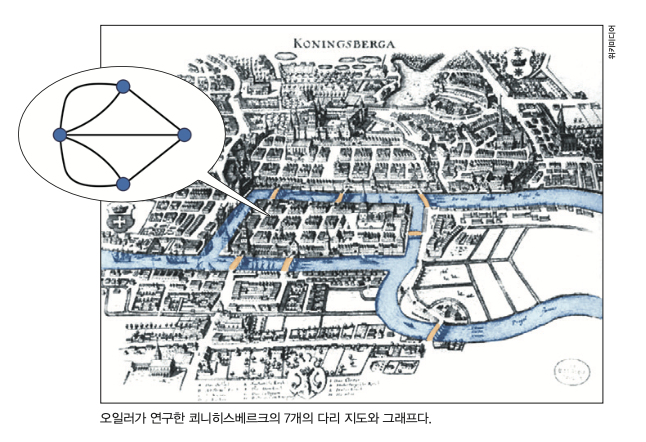
오일러가 수학에 공헌한 내용은 다양한데, 현대에 널리 사용되는 표기법을 만든 것이 대표적이다. 자연로그를 정의하는 상수 e를 만들었고, ‘쾨니히스베르크의 다리 문제’를 푼 것으로 잘 알려져 있다. 1736년 러시아 쾨니히스베르크 지역의 섬과 강변 사이에 놓인 7개의 다리가 있었는데, 이곳의 사람들이 한곳에서 출발해 다리를 한 번씩만 지나 제자리로 돌아올 수 있는지 궁금해했다. 이게 바로 ‘쾨니히스베르크의 다리 문제’다. 오일러는 점과 선을 이용한 그래프로 나타내 그렇게 이동할 수 없다는 사실을 알아냈다. 이는 수학의 한 분야인 ‘그래프 이론’으로 발전했다.
소수 계단을 상상한 오일러
정수론은 오일러의 천재성을 유감없이 발휘하는 데 더할 나위 없이 좋은 분야였다. 페르마가 현대 정수론의 기초를 닦았다면, 오일러는 이를 넓히고 여러 층을 쌓아 견고하게 만들었다고 할 수 있다.
오일러는 누구보다 소수를 사랑했다. 그는 소수가 나올 때만 높아지는 기묘한 계단을 상상했다. 소수가 나타날 때마다 한 칸 상승하고 그렇지 않은 구간에서는 평지로 이어지는 불규칙한 계단이다. 소수는 자주 나타나는 구간이 있지만, 10000000에서부터 10000100까지는 2개의 소수만 나타나는 것처럼 드물게 나타나는 구간이 있어 소수 계단의 모양은 불규칙하다. 오일러는 소수 계단을 머릿속으로 오르고 또 오르며 소수가 언제 나타나는지 살폈다.
그러다 오일러는 우연히 한 수학 문제를 푸는 과정에서 특이한 식과 답을 발견했다. ‘모든 자연수를 제곱해 그 역수를 무한히 더해 나가면 몇이 될까?’라는 문제다. 당시 스위스 바젤에 있던 스위스 수학자 야코프 베르누이는 여러 수학자에게 자기 자신을 포함해 장 베르누이, 다니엘 베르누이, 라이프니츠, 아브라암 드무아브르 등 위대한 수학자들이 문제 해결을 시도했으나 모두 실패했다고 이야기하며 문제를 풀어보라고 권했다. 그러면서 이 문제는 ‘바젤 문제’라는 이름을 갖게 됐다. 오일러는 1735년 이 문제를 해결하면서 일약 유명 인사가 됐다.

갑자기 등장한 π와 소수
그런데 오일러는 이 문제를 푸는 과정에서 놀라운 발견을 했다. 바젤 문제를 소수로 이뤄진 하나의 식으로 유도할 수 있었는데, 여기서 오일러를 당혹스럽게 만드는 수가 나타난 것이다.
바로 이 식의 결과가 자연계에서 가장 완벽한 도형으로 불리는 원을 나타내는 값, π와 관련이 있던 것이다. π 때문에 소수에 정말 자연의 비밀이 숨겨져 있는 것이 아닐까 하는 이야기가 나왔고, 여전히 그 비밀은 풀리지 않고 있다.

이 식은 정수론에서 또 다른 중요한 의미를 지닌다. 자연수로 이뤄진 식과 소수와 1로만 이뤄진 식이 공식에서 같아진다. 즉 자연수를 알기 위해 소수를 잘 알아야 한다는 점을 시사하고 있다. 소수만 알면 수의 성질을 모조리 알 수 있다고 말해도 과언이 아니라는 것이다.
오일러는 여기서 더 나아가 ‘오일러 곱셈공식’이라는 일반화된 식의 일부 값도 알아냈다. 그가 유도한 식을 일반화해 제곱 부분의 2를 어떤 자연수를 대입해도 되게 N으로 바꾼 식에서 N이 짝수일 때의 값을 모조리 알아낸 것이다. 그런데 천하의 오일러도 홀수일 때의 값은 알아내지 못했다.

이후 수학자들은 이 식을 발전시켜 한 함수를 연구했는데, 그 함수가 리만 가설의 핵심인 ‘제타 함수’다. 제타 함수는 오일러 곱셈공식에서 N에 실수와 허수(제곱하면 음수가 되는 수) 등 다양한 수를 대입할 수 있는 식이다. 여기에서는 N을 s로 표기한다. 복잡하지만 여기서는 딱 한 가지만 알아두자. 오일러의 소수 연구가 수학계 최대 난제인 리만 가설로 이어진다는 점 말이다.