d라이브러리

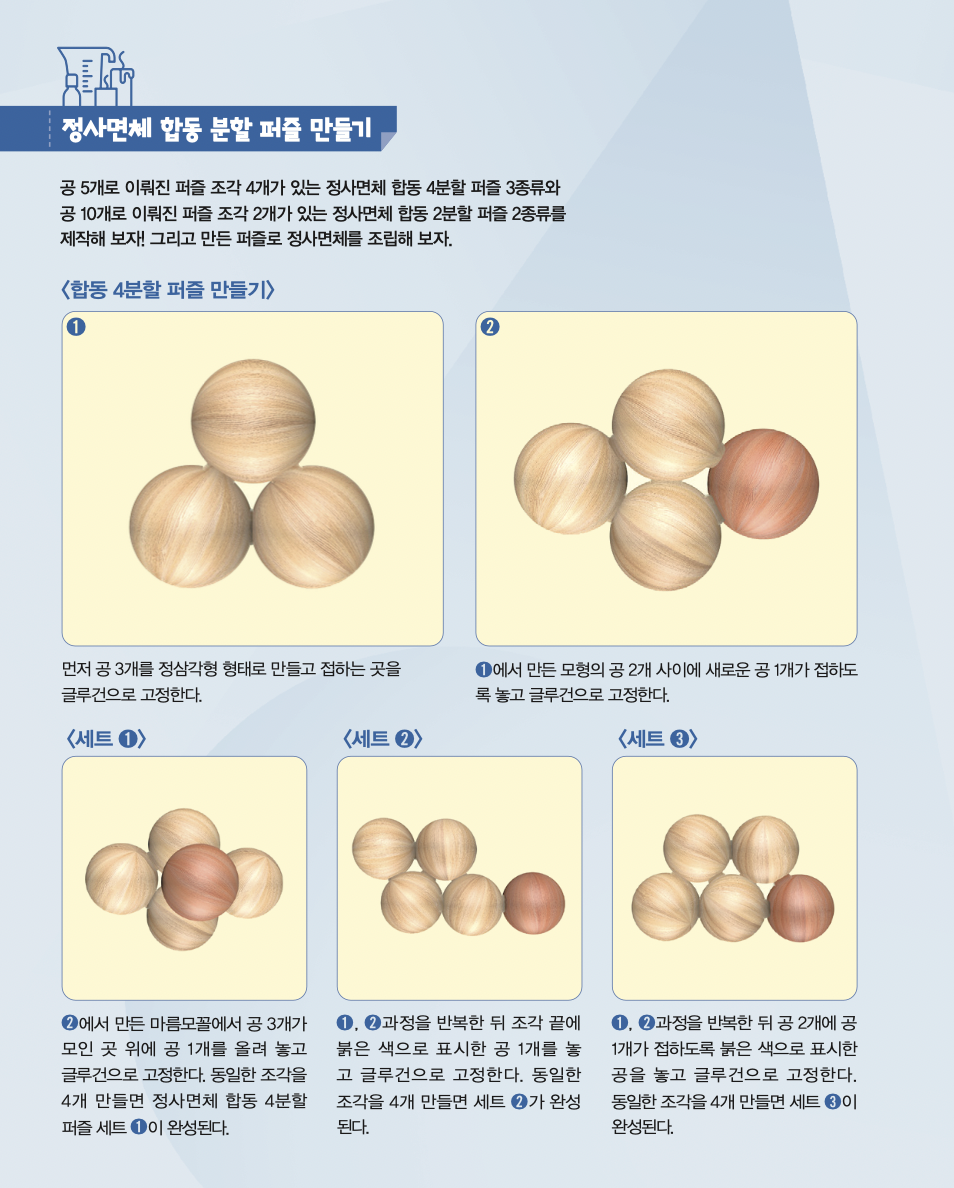
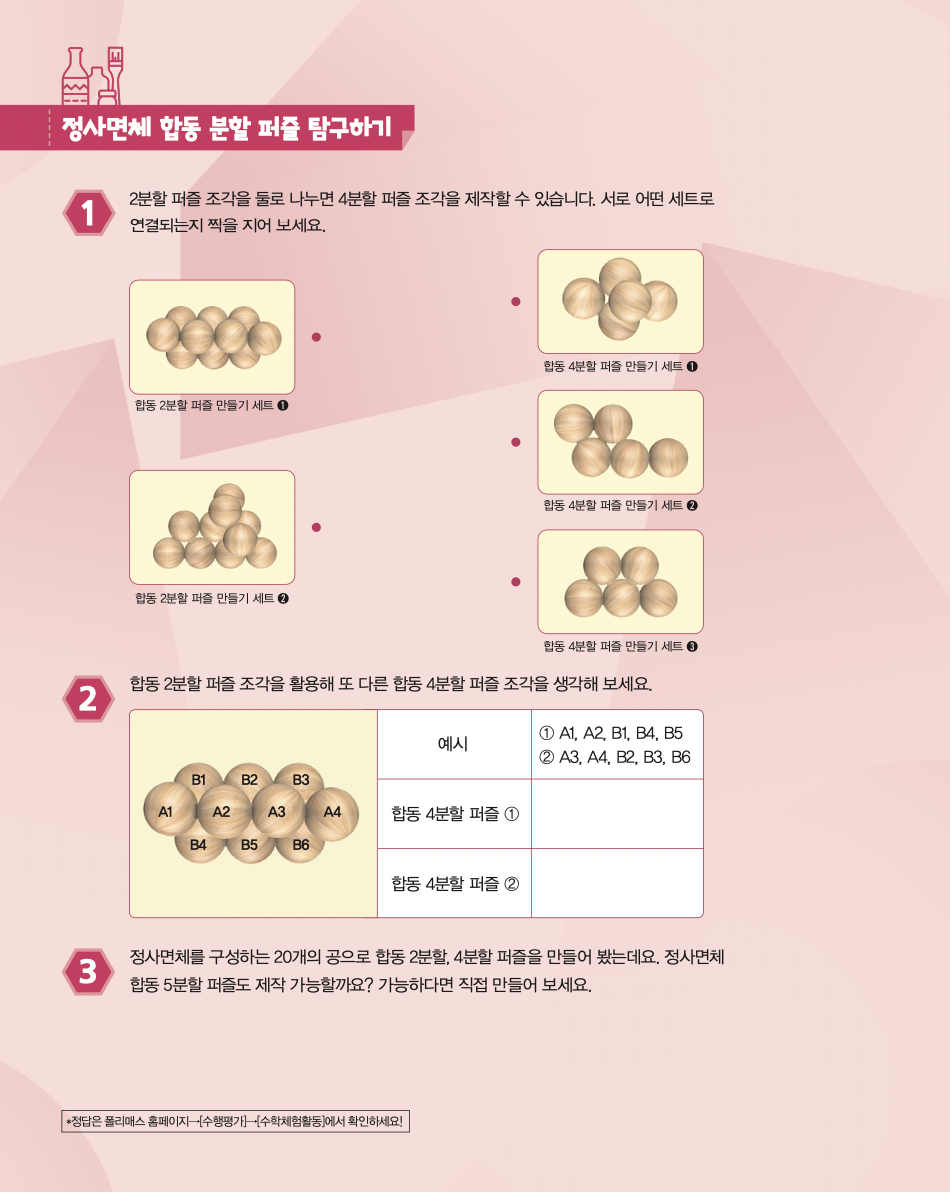
사과나 오렌지처럼 둥근 과일은 정사면체 구조로 쌓으면 일정한 공간에 최대한 많은 과일을 쌓을 수 있다. 이러한 구조에 관한 이해를 높이기 위해 ‘정사면체 합동 분할 퍼즐’을 직접 만들어 보자.

공을 빽빽하게 쌓는 방법, 케플러의 추측

17세기 천문학자이자 수학자인 요하네스 케플러는 3차원 공간에서 크기가 같은 구 여러 개를 가장 빽빽하게 배열하는 방법을 고민했다.

구의 밀집도를 높이는 대표적인 방법은 ‘육방 밀집 구조’와 ‘면심 입방 구조’가 있다. 육방 밀집 구조는 두 형태의 배열이 반복되는 A-B 구조, 면심 입방 구조는 세 가지 형태의 배열이 반복되는 A-B-C 구조라고 이해하면 쉽다.

먼저 구 3개가 정삼각형을 이루도록 여러 개의 구를 배열해 A층을 만든다. 그 위에 구 3개가 만드는 홈마다 공을 놓아 B층을 만든다. 두 층의 구가 겹쳐지지 않게 엇갈려 놓인다. 이제 그 다음 층을 만들어야 하는데, 여기서 육방 밀집 구조와 면심 입방 구조의 차이가 생긴다.

육방 밀집 구조에서는 A층과 구의 x좌표 위치가 같아 배열 형태가 똑같은 층을 쌓는다. 반면 면심 입방 구조에서는 3층에 A, B와 배열 형태가 전혀 다른 C층을 쌓는다. 즉 세 층의 구가 모두 엇갈린다. 단, 3개의 구가 정삼각형을 이뤄야 한다. 이렇게 육방 밀집 구조는 A와 B 형태의 층을 번갈아 쌓고, 면심 입방 구조는 A, B, C 형태의 층을 순서대로 계속 쌓는 구조다.

케플러는 면심 입방 구조와 육방 밀집 구조의 밀집도가 같음을 증명했다. 하지만 이 구조가 또다른 구조보다 밀집도가 높음을 수학적으로 증명하지 못해 ‘케플러의 추측’으로 자리 잡았다. 이후 387년 동안 많은 수학자가 이 문제에 도전한 끝에 1998년 토마스 헤일스 미국 피츠버그대학교 교수가 대용량의 컴퓨터를 이용한 계산을 통해 케플러의 추측을 증명했다.