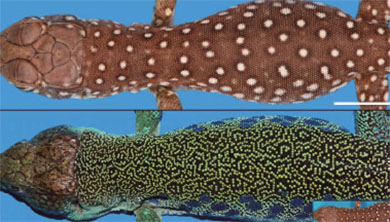
그래프의 채색 문제를 다루는 허준이 교수님의 연구부터 고차원에서의 공 쌓기 문제를 푼 마리나 비아조프스카 교수님의 연구까지! 다음 활동을 통해 2022 필즈상 수상자 네 분의 주요 연구를 살짝 엿보세요!
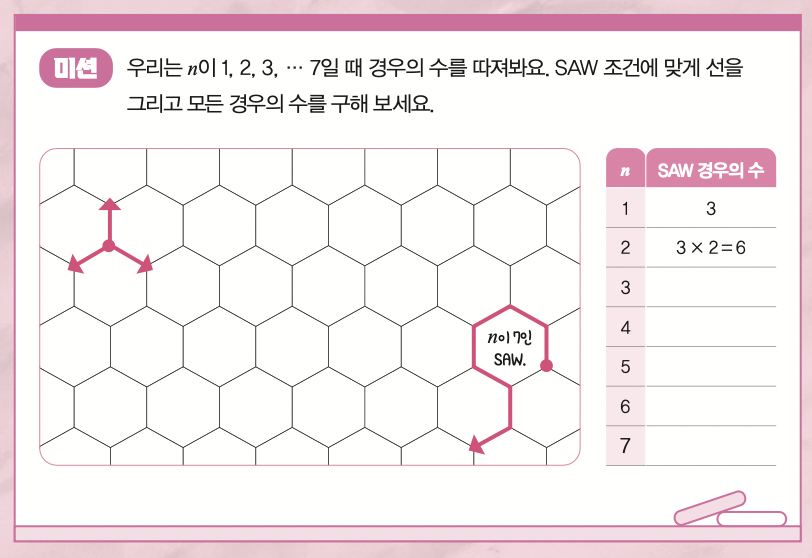
정육각형 격자 모형 위를 비틀거리며 돌아다니자!
위고 뒤미닐-코팽 교수는 격자 모형에서 ‘자기 회피 보행(SAW)’도 연구합니다. 말 그대로 자기가 한 번 걸어간 길은 다시 걷지 않으면서 움직이는 거예요. 정육각형 격자를 따라 선을 긋는 시행을 n번 합니다. 한 점에서는 세 방향으로 선분을 그을 수 있겠죠? 그런데 한 번 그은 선 위로는 다시 선을 그을 수 없다는 조건이 추가되면 첫 번째 선 이후로는 두 갈래길 중 하나를 무작위로 정해 선을 긋게 됩니다. 이렇게 그은 선을 SAW라고 해요. 뒤미닐-코팽 교수는 n이 커질 때 원점에서 출발한 SAW의 모든 경우의 수의 증가 속도를 연구했어요.
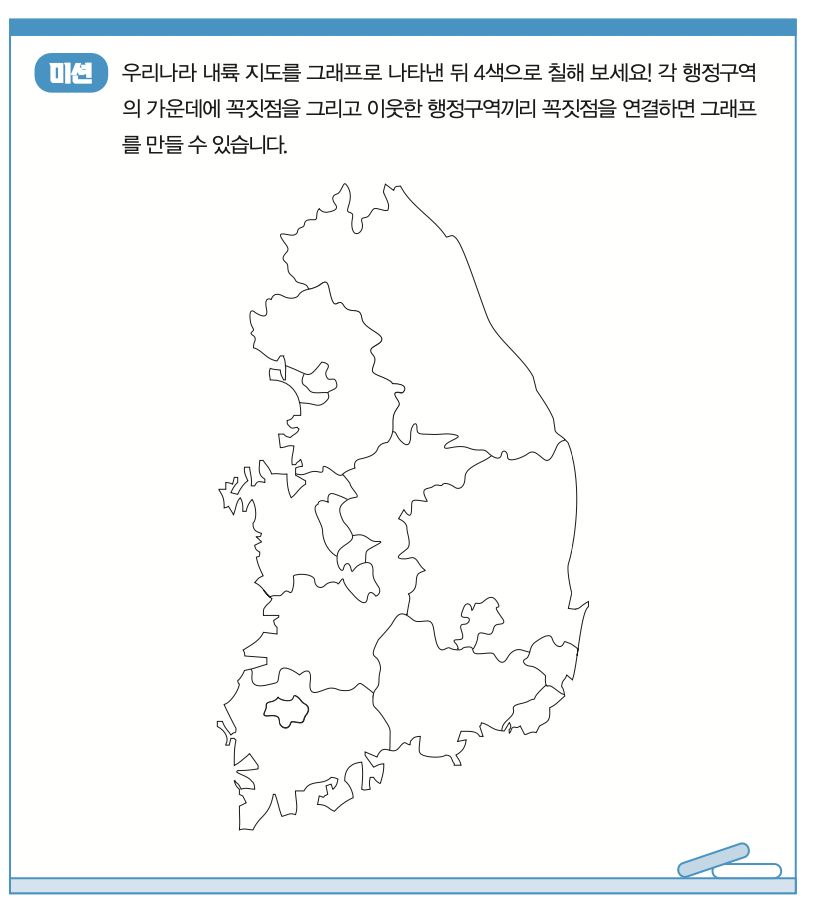
지도를 그래프로 나타내고 4색으로 색칠하자!
허준이 교수의 대표 업적인 ‘리드의 추측’은 그래프의 채색 다항식에 관한 성질을 밝힌 것이에요. 채색 다항식은 그래프의 연결된 두 꼭짓점은 다른 색으로 칠할 때 q가지 색으로 그래프 전체를 칠하는 경우의 수를 나타낸 식이지요. 그런데 모든 지도는 그래프로 나타낼 수 있고, 4색만으로 그래프 전체를 칠할 수 있어요. 이 문제가 수학계 유명한 난제였던 ‘4색 정리’예요.
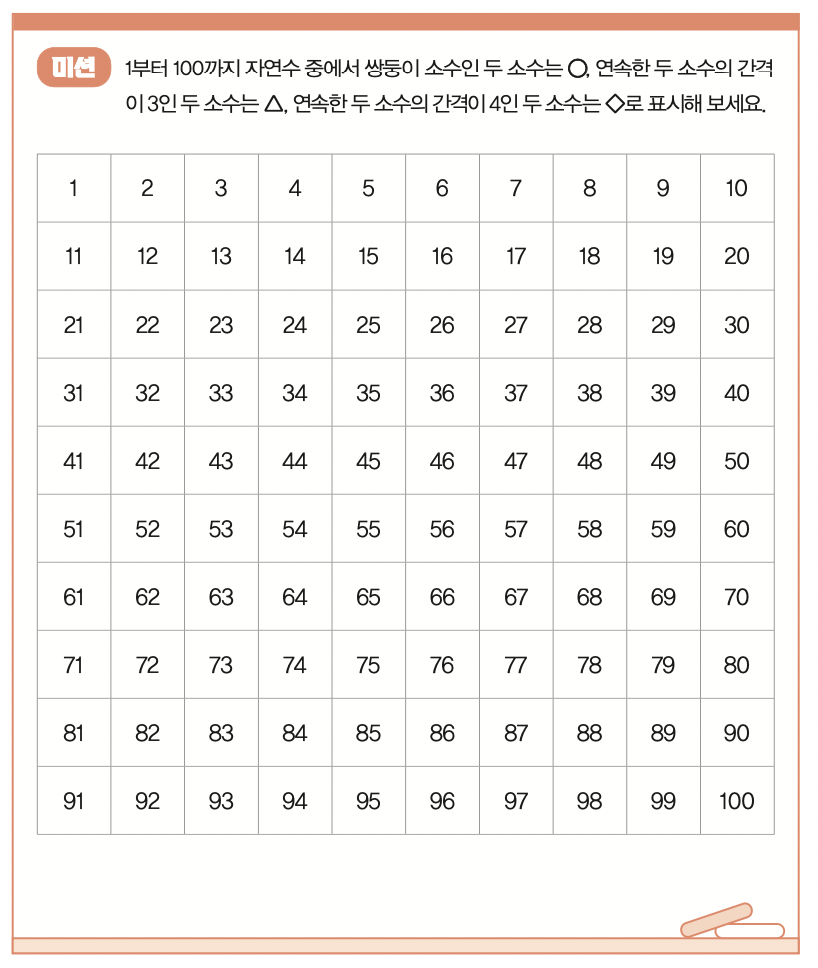
쌍둥이 소수를 구하라!
제임스 메이나드 교수는 ‘쌍둥이 소수 추측’과 관련한 문제에서 의미 있는 결과를 냈어요. 쌍둥이 소수 추측은 연속한 두 소수의 간격이 2인 소수 쌍은 무수히 많다는 추측이에요. 메이나드 교수가 참여한 폴리매스 프로젝트에서는 연속한 두 소수의 간격이 246 이하인 소수 쌍은 무수히 많다는 것을 밝혔어요.
구를 최대한 많이 쌓자!
마리나 비아조프스카 교수는 고차원에서 ‘케플러의 추측’을 해결했어요. 1611년 독일 수학자 요하네스 케플러는 3차원에서 구를 최대한 많이 쌓으려면 피라미드 형태로 쌓아야 한다고 추측해요. 이 문제는 1998년에 엄청난 컴퓨터 계산을 이용해 해결됐는데요. 비아조프스카 교수는 상상하기 어려운 공간인 8차원과 24차원에서의 케플러의 추측을 해결했어요. 우리는 3차원 공간에서 과일을 쌓아 비아조프스카 교수의 연구를 엿봅시다.