d라이브러리

H4가 돌아왔다! 할아버지 배우들의 배낭여행기를 다뤄 인기를 끌었던 예능프로그램 ‘꽃보다 할배’가 이번에는 스페인으로 떠났다. 일명 ‘꽃할배’들이 스페인에서 보내오는 이야기는 첫 방송부터 많은 시청자들의 관심을 모으고 있다. 그런데 꽃할배들의 여행을 자세히 들여다보면 곳곳에서 수학을 발견할 수 있다. 수학과 함께 꽃할배들의 스페인 배낭여행을 두 배로 즐겨 보자!

꽃할배 신드롬은 계속된다!

“칠순이 넘은 할아버지들이 떠나는 배낭여행!”

꽃보다 할배는 이런 발상의 전환으로 시작됐다. 황혼에 접어든 할아버지 배우들이 청년들처럼 유럽으로 배낭여행을 떠나면서 생기는 좌충우돌 여행기를 예능프로그램으로 제작한 것이다.

평균 연령 76세, 방송 경력을 합치면 200년이 넘는 원로배우들이 유럽을 누비며 보여 주는 예상 밖의 모습은 ‘신개념 예능’이라는 평가를 받았다. 70세 할아버지인 백일섭 씨가 막내라는 이유로 형님들에게 커피를 타서 대접하며 억울해 하고, 에펠탑 앞에서 청년들처럼 점프하며 사진을 찍는 모습은 많은 시청자들에게 신선한 재미를 선사했다.

반면 올해 나이 여든인 배우 이순재 씨가 열심히 공부하며 현지인에게 영어와 독일어로 대화를 시도하는 모습은 존경심을 불러일으키기 충분했다. 또 두 번째로 나이가 많은 신구 씨는 에펠탑을 바라보며 젊은이들에게 “실패하더라도 계속 도전하라”는 교훈을 남겼다. 이처럼 시청자들은 노 배우들의 말과 행동을 통해서 단순히 재미만이 아닌 인생의 연륜이 담긴 교훈을 배울 수 있었다. 여기에 만능 짐꾼 이서진이 동참하면서 꽃보다 할배는 동시간대 예능 프로그램 가운데 최고의 시청률을 올렸다.

꽃보다 할배가 흥행 대박을 일으키면서 중장년층의 여행기를 담은 다양한 예능프로그램이 뒤를 이었다. ‘꽃보다 할배 대만편’과 중년 여배우들의 유럽 여행기를 담은 ‘꽃보다 누나’ 등이 계속해서 인기를 끌었다. 그리고 이 같은 인기는 중장년층의 해외여행 증가로 이어졌다. 실제로 한 대형 여행사는 전체 해외여행 고객 중 40대 이상 연령층이 전년도에 비해 3% 증가했다고 밝혔다.

이처럼 지난 한 해 동안 화재를 모은 꽃보다 할배는 방송이 끝나기 무섭게 다음 여행에 대한 기대가 높았다. 그리고 드디어 3월 초부터 스페인 여행기를 담은 꽃보다 할배 시즌2가 방송되기 시작했다!

할배들이 세계 모든 도시를 방문하려면?

꽃할배들은 전편에서 프랑스, 스위스, 독일과 대만의 14개 도시를 여행했다. 그리고 이번 스페인 여행에서는 바르셀로나와 그라나다, 세비야와 마드리드, 그리고 스페인의 이웃나라인 포르투갈의 수도 리스본을 방문했다. 그런데 할배들은 지난 시즌과 달리, 이번에는 여행 일정까지 알아서 계획해야 한다는 미션을 받았다. 이에 첫 방송에는 할배들이 한자리에 모여서 여행 정보와 지도를 확인해가며 세세한 일정을 짜는 모습이 나온다.

그런데 만약 할배들이 전세계 모든 도시를 여행한다면 어떻게 방문 일정을 짜야 가장 효율적으로 여행을 할 수 있을까? 수학자들은 다소 엉뚱해 보이는 이 문제의 답을 찾기 위해 무려 80년 동안이나 연구를 해오고 있다. ‘외판원 문제’라고도 불리는 이 문제는 다음과 같이 정의된다.

“여러 도시들이 있고, 한 도시에서 다른 도시로 이동하는 거리가 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 가장 짧은 경로는 무엇인가?”

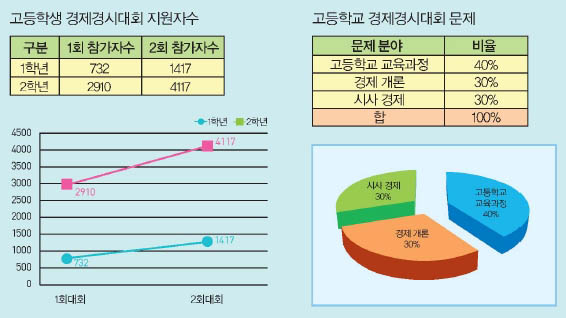
수학자들이 이 문제에 관심을 갖고 연구하기 시작한 것은 1930년대부터다. 단순히 생각하면 가능한 모든 경우의 수를 나열한 뒤, 가장 짧은 경로를 선택하면 될 것 같다. 그런데 이 경우 도시가 세 개일 때는 2개의 경우밖에 없지만, 도시의 수가 많아질수록 경우의 수가 기하급수적으로 늘어난다. 도시 수가 24개만 돼도 가능한 모든 경로의 수가 9407경 3336조 개나 되고, 초당 1000억 번의 계산을 할 수 있는 컴퓨터를 사용해도 모든 경로를 찾는 데 30년이나 걸린다. 따라서 수학자들은 다양한 방법으로 이 문제의 정답을 찾는 한편, 가장 정답에 가깝다고 여겨지는 ‘근사해’를 찾는 방법을 함께 연구하고 있다.

그런데 수학자들은 왜 이런 문제를 연구하는 걸까? 대수롭지 않아 보이는 이 문제는 사실 현대 산업의 다양한 문제를 해결하는 데 쓰인다. 전세계 곳곳의 공항에서 매일 출발하고 도착하는 항공기의 비행 계획이나, 정해진 공간 안에 최대한 많은 전기회로를 집어 넣어야 하는 반도체 설계 등의 문제를 풀 때 활용된다.

비행기 탑승 시간도 수학으로 빠르게!

꽃할배들은 이번 여행에서 처음부터 여러 가지 난관에 봉착한다. 그 중 하나가 늘 동행했던 이서진 씨 없이 비행기를 타고 스페인 바로셀로나의 숙소까지 찾아가야 하는 것이었다. 시청자들은 영어가 서툰 할배들이 비행기 수속과 탑승, 그리고 입국 수속까지 마치는 과정을 조마조마한 마음으로 바라봤다. 결국 할배들은 우여곡절 끝에 바로셀로나의 숙소에 도착할 수 있었다.

그런데 이렇게 할배들이 서울에서 바르셀로나까지 찾아가는 과정에도 알고 보면 재미있는 수학 원리가 숨어 있다. 바로 ‘비행기 탑승 순서’ 문제다.

비행기를 탈 때는 보통 일등석과 비즈니스석 승객들이 먼저 탑승한 뒤, 나머지 승객들이 줄을 서서 탑승한다. 200~300명의 승객들이 한두 줄로 비행기 안으로 들어가서 자리를 잡다 보니 모두 탑승하기까지 수십 분 이상 걸린다. 더 효율적인 탑승 방법이 없을지 고민하던 미국 페르미연구소 소속 물리학자 제이슨 스테펜은 승객들이 탑승할 때 시간이 지연되는 원인을 찾아봤다. 그리고 크게 두 가지 원인이 있다는 것을 알게 됐다.

첫 번째는 짐을 올리기 위해 복도에 서 있는 동안 뒷사람이 움직이지 못하면서 생기는 지연이다. 그리고 두 번째는 2~4개씩 붙어 있는 좌석에서 자기 자리를 찾아갈 때, 이미 앉아 있는 사람과 부딪치면서 생기는 지연이다.

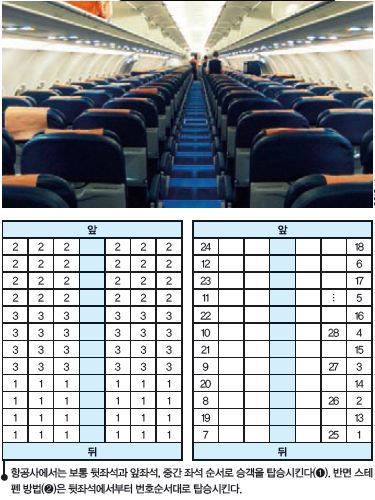
스테펜은 항공사들이 승객을 탑승시키는 모든 방법을 따져 본 뒤, 일명 ‘스테펜 방법’이라고 하는 효과적인 방법을 개발했다. 스테펜 방법에서는 승객들을 창가자리와 가운데 좌석, 그리고 복도쪽 좌석으로 나눈 뒤에 비행기의 가장 뒤쪽부터 창가쪽 승객을 먼저 태운다. 이후 가운데 자리, 그리고 복도쪽 자리 승객을 순차적으로 탑승시킨다.

이 방법을 알고리즘으로 만들어 컴퓨터로 계산한 결과, 승객들을 앞부터 채우는 방법에 비해 4~10배나 빠르게 승객을 탑승시킬 수 있는 것으로 나타났다.
 
가우디 건축은 스페인 수학의 자부심!

배낭여행의 ‘꽃’은 뭐니뭐니해도 여행지에서 만난 아름다운 풍경과 문화유산이다. 그런데 만약 수학자들에게 스페인 수학 유산을 한 가지만 꼽으라고 하면 아마도 이구동성으로 ‘가우디의 건축’이라고 답할 것이다.

가우디는 비록 수학자가 아닌 건축가였지만, 천재적인 발상으로 건물에 수학을 담았다. 특히 사그라다 파밀리아 성당은 현수선과 마방진 등의 수학적인 요소를 곳곳에서 발견할 수 있는 걸작이다.

우선 성당의 외관을 보자. 밖에서 본 성당은 마치 원기둥 위에 원뿔을 얹어놓은 듯한 네 개의 커다란 기둥이 눈에 들어온다. 가우디는 이 기둥의 모양을 ‘현수선’을 이용해서 설계했다. 현수선은 양쪽 끝이 고정된 선을 늘어뜨렸을 때 생기는 곡선으로, 현수교에서 쉽게 볼 수 있다. 모래주머니를 실에 매달아 늘어뜨렸을 때도 현수선이 생기는데, 가우디는 그 곡선을 그대로 본떠서 성당을 설계했다. 현수선이 무게를 안정적으로 나누는 구조이기 때문이다.

또한 사그라다 파밀리아 성당의 마방진은 가우디가 성당의 정체성을 표현하기 위해 암호처럼 감춰 놓은 수학적인 상징이다. 가로, 세로, 대각선 방향으로 숫자를 더했을 때 각각 33이 되는 이 마방진은 예수 그리스도의 죽음과 부활을 기념한다. 그리고 중복된 숫자 10과 14를 더하면 48이 나오는데, 48은 9+13+17+9로 나타낼 수 있다. 이 숫자를 라틴어 알파벳 순서에 대응해 보면 I(9), N(13), R(17), I(9) ‘INRI’라는 단어가 만들어진다. ‘나사렛 예수, 유다의 왕’이라는 뜻이다.
 
현대 수학의 결정체, 피카소의 미술작품!

꽃할배가 여행한 스페인에서 만날 수 있는 또 하나의 특별한 수학 유산은 바로 피카소의 작품이다. 20세기 최고의 화가로 손꼽히는 피카소는 스페인에서 태어났다. 비록 프랑스에서 주로 활동했지만, 그는 조국에 대한 관심을 다양한 작품으로 표현했다. 그래서 바르셀로나에는 피카소의 작품을 한데 모아 전시하는 ‘피카소 미술관’이 있다.

피카소의 작품을 볼 때 가장 눈여겨볼 부분은 ‘관점’이다. 피카소는 2차원 평면인 캔버스 위에 여러 가지 시점에서 바라본 대상의 모습을 하나로 표현했다. 보기에 따라서는 괴기스럽게 느낄 수 있지만, 피카소의 작품을 연구하는 학자들은 이 같은 표현 방법이 현대 수학의 새로운 공간 개념에서 영감을 받은 것이라고 설명한다. 피카소가 활동할 당시 프랑스의 수학자 앙리 푸앵카레는 3차원의 공간에 시간을 덧붙인 4차원 시공간을 제안했다. 피카소가 2차원 평면에 3차원의 다양한 시점을 동시에 표현한 점과 일맥상통한다.
 
피카소의 작품 중에서도 단연 눈에 띠는 작품은 ‘게르니카’다. 게르니카는 가로세로 777cm×349cm에 이르는 거대한 작품으로, 제2차세계대전 당시 스페인의 작은 도시 게르니카에서 일어난 독일군의 민간인 학살을 그림으로 표현했다. 피카소는 이 작품에서 죄없는 사람들을 짓밟은 범죄에 대한 분노를 표현했다. 이뿐만 아니라, 당대 수학자들이 연구한 공간에 대한 새로운 해석과 함께 이등변삼각형의 대칭 구조를 활용해 예술적 가치를 더했다.

이제부터 꽃보다 할배를 시청하는 <;수학동아>; 독자들은 스페인에서 펼쳐지는 꽃할배들의 여행기에서 ‘수학’에 주의를 기울여 보자. ‘아는 만큼 보인다’는 말처럼, 꽃할배들의 여행에 특별한 감동이 더해질 것이다.