d라이브러리

확률 개념이 적용된 AI를 이해하기 전에 우선 확률의 기본적인 정의부터 조건부확률, 확률분포까지 살펴볼게! 다음 장으로 페이지를 넘기면 확률분포를 적용하는 AI의 학습 알고리듬을 알 수 있어.

1 경우의 수

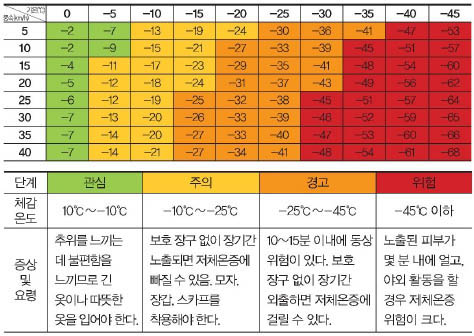
특정 사건이 일어날 가짓수를 경우의 수라고 합니다. 주사위를 던지면 1부터 6까지 나올 수 있으므로, 6가지 경우의 수가 생깁니다. 경우의 수를 구하는 방법은 두 가지예요. 우선 A와 B 두 사건이 동시에 일어나지 않을 땐 A와 B가 일어나는 경우의 수를 모두 더해 구합니다. 예를 들어 집에서 학교로 가기 위해 버스를 타는 방법이 3가지, 지하철이 2가지라면 모든 경우의 수는 5가지이죠.

이와 달리 A와 B가 잇달아 일어나는 경우의 수는 각각의 사건이 가진 경우의 수를 곱하면 됩니다. 
동전 1개, 주사위 1개를 잇달아 던진다면 나올 수 있는 모든 경우의 수는 2×6, 즉 12입니다.

2 순열과 조합 

AI가 사용할 데이터들은 정리가 필요합니다. 1번 데이터와 2번 데이터의 순서가 중요한 경우와 그렇지 않은 경우가 있을 겁니다. 수학에서도 잇달아 일어나는 사건의 경우의 수에서 순서를 고려하기 위해 순열(P)과 조합(C)의 개념을 만들었어요. 

서로 다른 n개의 데이터 중에서 r개를 선택해 순서대로 늘어놓는 것을 순열이라 하며 _nP_r로 표시합니다. 순열 공식 _nP_r = n(n-1)(n-2)…(n-r+1)이고 이때 n≥r이며, _nP₀의 값은 1로 정의합니다. 반면 n개의 데이터 중 순서를 생각하지 않고 r개를 뽑는 것을 조합이라고 합니다. 조합 공식 _nC_r =_nP_r/r!  이때 r!은 1부터 r까지의 자연수를 곱한 값이며, 0!과 _nC₀의 값은 모두 1로 정의합니다.

3 빈도적 확률 

우연에 지배되는 어떤 사건 A가 일어날 가능성을 A에 대한 수학적 확률이라고 하며 P(A)로 표시합니다. 주사위를 던졌을 때 1이 나올 확률은 1이 나올 경우의 수를 전체 경우의 수로 나눈 값인 1/6이 됩니다.

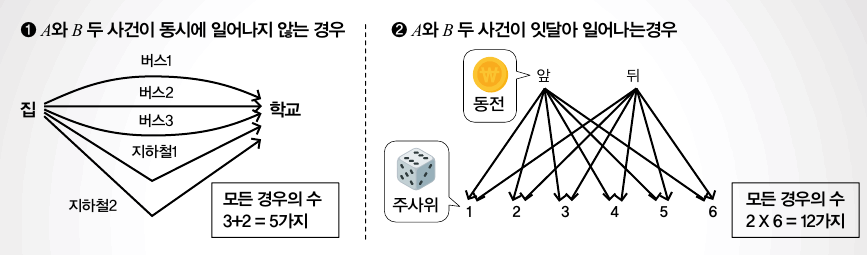
4 조건부확률 

두 사건 A, B가 일어나는 상황을 떠올려볼게요. 예를 들어 어떤 학급의 전체 학생 60명 중 남학생이 35명이고 안경을 낀 남학생은 10명이라고 해보죠. 이 학급에서 남학생을 뽑았을 때 안경을 끼고 있을 확률은 어떻게 구할 수 있을까요? 이때 남학생을 뽑는 사건은 A라고 하고 안경을 낀 남학생을 뽑는 사건을 B라고 할 수 있습니다. 즉, 사건 A가 일어났을 때 사건 B가 동시에 일어날 확률을 사건 A에 대한 사건 B의 조건부확률이라 하고 P(B|A)라고 나타냅니다. 이를 처음으로 제시한 영국의 수학자이자 신학자 토마스 베이즈의 이름을 넣어 베이즈 확률(정리)로도 불립니다.

5 확률변수와 확률분포 

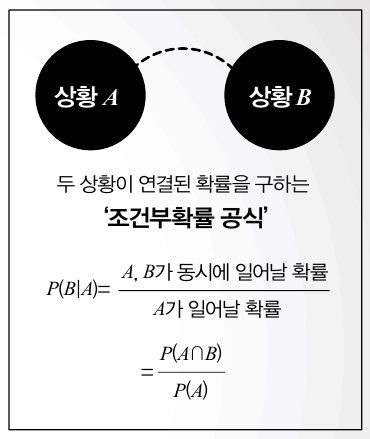
우리 주변에서 일어나는 사건들의 변수가 무엇인지, 그 변수가 현실에서 어떤 분포로 발생하는지 알아야 합니다. 이를테면 한쪽 면에는 1이, 다른 면에는 2가 새겨진 동전 두 개를 동시에 던질 때 나오는 수의 합을 하나의 확률변수 X라고 해볼게요. 이때 나올 수 있는 모든 경우의 수는 (1, 1), (1, 2), (2, 1), (2, 2)이며 두 숫자를 더한 값인 X는 2, 3, 4의 값을 취할 수 있습니다. 이때 2가 나올 확률은 , 3이 나올 확률은 , 4가 나올 확률은 이죠. X가 가질 수 있는 값과 그 값이 나올 확률을 정리한 표를 확률분포라고 합니다. X가 취하는 값이 n개이면 그에 따라 나오는 확률의 값도 그에 따라 늘어납니다.

똑같은 질문? 다른 답변! 
확률 알고리듬이 결정한다

확률의 기본 개념을 배웠으니 이제 AI가 불확실성을 줄이고 의사결정에 도움을 줄 수 있는 최적화된 답안을 찾는 과정을 살펴볼게. 앞에서 나온 확률 알고리듬을 정리한 내용이니까 복습하는 의미로 읽어보면 좋아!

1단계 | 데이터 해석하기

음성, 이미지, 텍스트 등의 데이터가 AI에 입력되면 AI는 이를 벡터함수로 받아들입니다. 이제 AI는 각각의 목적에 맞는 최적의 답안을 찾기 위해 움직여야 합니다. 스마트폰 사용자가 대화형 AI인 미스터 수동에게 ‘아이유의 최신 노래가 듣고 싶다’고 말했다고 해봅시다. 4월호에서 본 것처럼 입력된 음성의 특징을 파악하기 위해 주파수별 신호를 분해해 나열한 다음, 자연어 알고리듬에 따라 신호의 의미를 파악합니다.

2단계 | 확률 알고리듬 설정하기

① 빈도적 확률 알고리듬

데이터 X는 가수 이름입니다. 알고리듬에 들어갈 확률 모형을 설정하는 변수 세타(θ)는 특정 값으로 지정됩니다. 이는 가수 A라는 데이터가 들어오면 최신곡은 a라고 지정해주는 고정값입니다. 알고리듬마다 θ를 정하는 기준은 다를 수 있습니다.

② 베이즈 확률 알고리듬

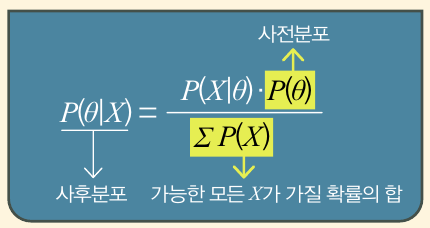
데이터 X는 역시 가수 이름입니다. 그런데 알고리듬에 들어갈 확률 모형을 설정하는 변수 세타(θ)가 고정값이 아닌 자신만의 확률분포를 갖습니다. 이를 사전 분포라고 합니다. 아래 식처럼 우리가 현실에서 관측한 데이터와 직접 설정한 사전 분포에 따라 구한 사후분포의 값이 우리가 찾으려는 값입니다. 이때 분모에 있는 모든 데이터가 가질 확률의 합을 계산하기가 어려워 이를 쉽게 하기 위한 방법이 연구되고 있습니다.

3단계 | 최적화하기

수학에서 최적화한다는 것은 미분을 통해 극값을 찾아가는 과정입니다. 즉, 기울기가 0인 부분을 찾는 거죠. 이를 경사 하강법이라 부르는데요. AI 학습 알고리듬은 처음 입력된 데이터를 해석하거나 이를 통해 답을 찾아갈 때 모두 경사 하강법을 사용합니다. 여러 데이터는 알고리듬 내에서 여러 겹의 행렬층으로 존재하는데요. 미분으로 각 행렬층의 데이터에 대한 오차를 계산해 오차범위 밖의 값을 가지는 층의 데이터를 제외하거나 전체 데이터의 오차를 최소화하는 방식 등으로 적용되고 있습니다.

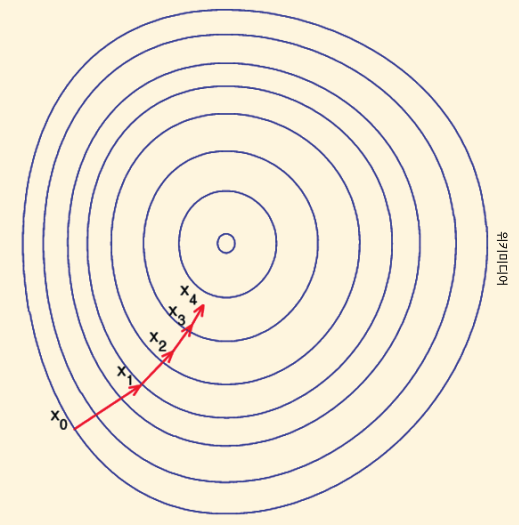
위 그림은 미분을 통해 최적의 해를 찾아가는 과정을 그린 모식도 입니다. 고리 모양은 알고리듬이 풀어낸 다양한 답안을 담고 있는 행렬층을 의미하고요. 우리가 최적의 답을 찾아가는 과정을 표현한 함수 f(x)에 대해 가장 먼저 시작점(초기 답안) x0를 정합니다. 현재 xi라는 값이 주어지면 그 다음으로 이동할 값은 xi+1이 됩니다.  위 그림에서 x0에서 x4로 나가는 것과 같습니다. 각 시행마다 이동하는 거리를 변수로 두고 알고리듬을 돌리면 최적의 답안이 있는 행렬층으로 다가서게 됩니다.

4단계 | 결괏값 추출하기

4월 9일 기준 삼성전자의 빅스비에게 ‘아이유의 최신곡을 틀어줘’라고 말하면 음원사이트인 벅스를 통해 아이유의 ‘Flu’라는 곡을 틀어줍니다. 100번을 시행해도 그 답이 변하지 않습니다. 이날 벅스의 음원 차트 1위가 아이유의 라일락임에도 말이죠. 이는 빈도적 확률 알고리듬에 따라 아이유의 최신곡에 대한 값이 Flu로 지정돼 있기 때문입니다. 현재 산업계는 계산 복잡도가 낮은 빈도적 확률 알고리듬을 많이 씁니다. 만약 베이즈 확률 알고리듬을 적용했다면, 사용자가 같은 요청을 했다고 해도 다른 곡을 선정해 보여줬겠지요.