d라이브러리

코로나19가 길어질수록 집안에서 즐길 수 있는 퍼즐이 더욱 빛을 발하고 있습니다. 누구나 하나쯤은 가지고 있을, 없어도 쉽게 만들 수 있는 칠교 조각으로 불가사의한 현상을 함께 탐구해봅시다.

※ 편집자 주
KPP(한국 퍼즐 파티)는 ‘퍼즐을 좋아하는 사람들의 모임’입니다. 저희의 퍼즐 이야기를 통해 신기한 퍼즐과 그 속에 숨은 수학을 즐겨보세요!

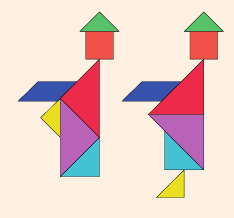
‘탱그램(Tangram)’이라고도 부르는 ‘칠교놀이’는 정사각형을 7개의 다각형 조각으로 나눈 다음 그 조각들을 조합해 다양한 형태의 모양을 만드는 퍼즐입니다. 아래 그림은 19세기에 활동한 유희 수학자 헨리 듀드니가 고안한 ‘두 명의 수도승’ 퍼즐입니다. 좌우 그림을 잘 관찰해보면 동일한 7개의 칠교 조각으로 수도승 모양을 만들었지만, 조금 다른 것을 알 수 있습니다. 한쪽 수도승은 다리가 있고, 다른 쪽 수도승은 다리가 없습니다. 같은 칠교 조각을 남김 없이 모두 사용했는데 왜 이런 현상이 발생하는 걸까요? 그 이유는 칠교 조각을 다른 방법으로 배치해 다리만 빼고 비슷한 모양을 만들었기 때문입니다. 자세히 보면 몸통의 길이가 다르죠. 이런 현상을 ‘칠교판 역설’이라고 부릅니다.

두 명의 수도승 이외에도 칠교판 역설이 나타나는 모양은 무척 많답니다. 착시 예술가 잔니 사르코네가 만든 퍼즐들이 대표적인 예입니다(오른쪽 칠교판 역설 퍼즐). 각각의 모양을 만들어보면서 모양 차이가 생기는 이유를 생각해보세요.

칠교판 역설과 비슷한 것으로, 19세기에 활동한 유희 수학자 샘 로이드가 고안한 ‘샘 로이드의 역설적 분할’이 있습니다. 아래 그림처럼 정사각형을 분할한 4개의 조각을 배치만 다르게 했을 뿐인데 면적이 늘었다 줄었다 합니다. 이런 종류를 ‘도형 분할 역설’이라고 한답니다.  

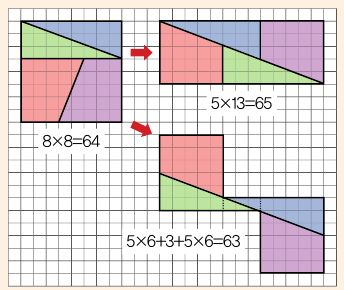
칠교판 역설이 미세한 ‘길이 차이’ 때문에 발생했다면 이 현상의 원인은 미세한 ‘기울기의 차이’입니다. 네 조각의 도형은 두 쌍의 합동인 도형으로 이뤄져 있는데, 빗변의 기울기가 각각 5/2(=2.5)와 8/3(=2.666…)입니다. 기울기가 비슷한 조각들을 마치 같은 것처럼 교묘하게놓았기 때문에 면적이 다르게 보이는 것입니다. 이렇게 비슷한 기울기를 만들 수 있는 수열로는 1, 1, 2, 3, 5, 8, 13, …으로 계속되는 ‘피보나치 수열’이 있습니다. 앞의 두 수를 더하면 다음 수가 나오는 규칙으로 만들어지는 수열로, 연속하는 두 수의 비율이 황금비인 약 1.618에 가까워지지요. 이렇게 미세하게 다른 기울기를 이용하면 누구나 도형 분할 역설을 만들 수 있답니다.