d라이브러리

수학에서 대칭은 좌우 대칭, 거울 대칭처럼 모양에 대한 대칭뿐 아니라 대상을 회전하거나 이동해 움직여도 그 모양이나 성질이 변하지 않는 것을 뜻합니다. 그리고 그런 관계에 있는 대상을 ‘군’, 이를 연구하는 분야를 ‘군론’이라 부르죠. 우리 주위 다양한 곳에 대칭이 있듯 수학에도 여러 종류의 군이 존재하는데요, 이번 화에서는 제 연구 분야인 군론을 조금이라도 엿볼 수 있게 각양각색의 군을 소개합니다.

가장 먼저 소개할 군은 ‘n차 대칭군’ S_n입니다. 닐스 헨리크 아벨과 에바리스트 갈루아가 밝힌 ‘5차 방정식의 근의 공식에 관한 연구’의 핵심이었던 바로 그 군인데요, 이 군을 이해하는 가장 쉬운 방법은 카드를 뒤섞는 ‘대칭이동’을 생각하는 겁니다.

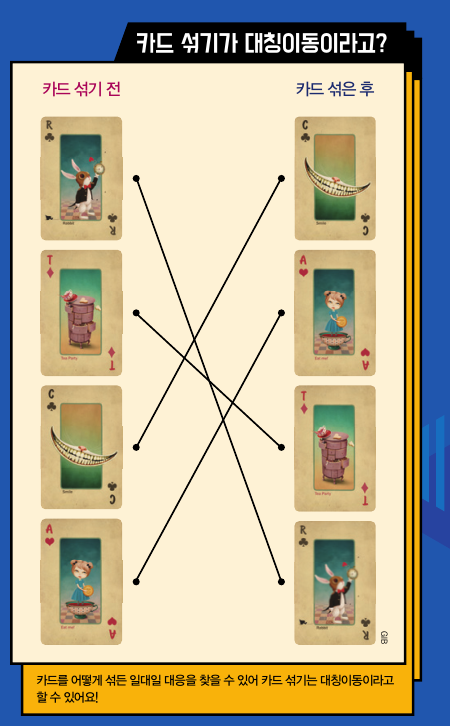
카드 섞기가 어떻게 대칭이동이 되냐고요? 카드를 어떤 순서대로 섞든 항상 서로 간의 ‘일대일 대응’을 찾을 수 있기 때문입니다. 대칭이동이란 도형을 한 점 또는 직선에 대칭인 도형으로 옮기는 것인데, 이를 함수로 표현하면 일대일 대응이 되기 때문이에요.

여기서 일대일 대응이란 n장의 카드를 어떻게 섞어도 본래 카드와 중복 없이 짝지을 수 있는 관계를 말합니다, 수학적으로 표현하면 두 집합의 원소들이 중복 없이 모두 대응되는 관계를 뜻합니다. 즉 n차 대칭군은 원소의 개수가 n개인 어떤 집합 X에 대해 X에서 X로 가는 일대일 대응 함수들을 원소로 갖는 군이죠.

정다각형의 대칭이동, 이면군!

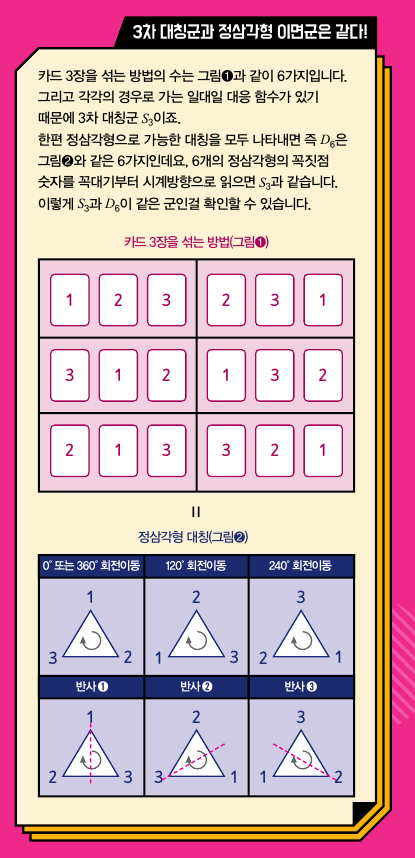
정n각형의 회전 대칭과 거울 반사 대칭을 모아놓은 군을 ‘이면군 D_2n’이라고 부릅니다. n차 대칭군 S_n은 정n각형 이면군 D_2n을 항상 부분군으로 갖는데요, 특별히 n이 3일 때는 대칭군과 이면군이 서로 같습니다. 

여기서 부분군이란 부분집합이라고 생각하면 쉽습니다. 집합 A={1, 2, 3, 4, 5}라고 하면 집합 B={1}이나 C={1, 2}처럼 집합 A의 일부분을 원소로 하는 집합을 집합 A의 ‘부분집합’이라고 합니다. 부분군 역시 어떤 군의 일부를 이루는 군이라고 보면 쉽습니다. 

3차원 결정의 대칭 구조를 분석하는 공간군!

자연에서 찾을 수 있는 대칭 구조에는 어떤 것이 있을까요? 겨울에 찾아오는 정육각형 대칭, 눈 결정이 있습니다. 눈 결정이 이런 대칭 구조를 갖는 이유는 H₂O, 즉 산소와 수소로 이뤄진 물 분자가 얼면서 정육각형 대칭 구조를 이루기 때문입니다.

눈 결정처럼 자연에서 볼 수 있는 결정들은 대부분 강력한 대칭 구조를 띠고 있습니다. 외부의 힘이 작용하지 않는 안정적인 상태에서 분자들이 균형을 이루고 있기 때문이에요. 이처럼 3차원에서 분자가 이룰 수 있는 대칭 구조들을 모아놓은 군을 ‘공간군’이라고 합니다. 수학자는 군론을 활용해 3차원에서 존재할 수 있는 결정의 대칭 구조가 총 230개임을 증명했습니다. 이 결과를 통해 화학자는 새로운 결정을 예측하죠.

예를 들어 새로운 결정의 한 단면을 엑스레이를 통해 촬영한다고 가정해봅시다. 이 단면을 통해 우리는 결정의 분자구조가 어떤 대칭 성질을 갖고 있는지 알 수 있습니다. 하나의 단면만 가지고는 정할 수 없지만, 여러 방향에서 촬영한 단면을 합하면 이 결정구조에 해당하는 대칭을 공간군에서 찾을 수 있습니다. 마치 ‘위에서 본 모습, 앞에서 본 모습, 옆에서 본 모습’을 통해 도형의 모양을 유추하는 것처럼요. 공간군을 활용한 3차원 대칭 분석은 화학뿐만 아니라 단백질 구조 분석을 하는 생물학에서도 쓰이며, DNA 이중나선 구조를 찾는 데에도 쓰이고 있습니다. 

끝나지 않는 군의 세계

이렇게 직접 관찰할 수 있는 군 외에도 수학적으로 정의한 추상적인 군이 군론에는 무수히 많습니다. 그리고 지금 본 것처럼 수학 본연의 연구부터 물리, 화학, 생물, 나아가 미술과 문화까지 군론을 활용하고 있죠. 앞으로도 계속 새로운 군이 발견되고 연구되겠죠?