

으아앗! 아름다워! 너무 그럴싸하지 않나요? 제가 완성하고도 놀랐다니까요? 그런데 왜 유명하지도 않은 할그림스키르캬를 만들었냐고요? 수학과 출신인 퓨처킴 눈에는 수학과 관련된 것들만 보이거든요(음하하). 이 교회를 본 순간 ‘구분구적법’이 딱 떠올랐답니다. 구분구적법은 고등학교에서 배우는 내용이니 잘 모르는 친구도 있겠네요. 하지만 한자의 뜻만 잘 풀어도 바로 이해할 수 있습니다.
구분할 구, 나눌 분, 구할 구, 쌓을 적
구분구적법은 면적을 구하기 어려운 도형을 직사각형 같은 기본도형으로 일정하게 나누고 그것들의 넓이를 더해 원래 도형의 넓이을 구하는 방법입니다. 곡선으로 둘러싸인 부분의 넓이는 어떻게 구해야 할지 막막하잖아요. 그럴 때 구분구적법을 쓰는 거죠.
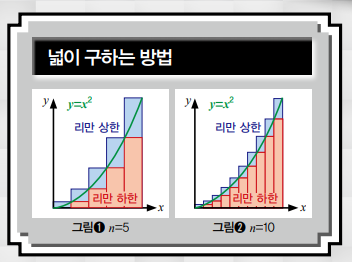
어떻게 넓이를 구하는지 알아볼게요. 그림①에서 이차함수 y=x² 그래프의 아랫 부분의 넓이를 구하려면, 먼저 밑변과 높이만 알면 쉽게 넓이를 계산할 수 있는 직사각형으로 구하고자 하는 넓이의 영역을 나눠야 합니다. 이렇게 구한 직사각형의 넓이를 모두 더하면 정확하지는 않아도 구하고 싶은 넓이와 비슷한 값을 구할 수 있죠.
더 정확한 넓이를 구하려면 그림②처럼 밑변이 더 짧은 직사각형으로 나누면 됩니다. 이렇게 밑변을 계속 줄여 나가다 보면 아주 작은, 거의 0에 가까운 직사각형으로 쪼개집니다. 이때 사용하는 개념이 바로 ‘극한’입니다. 극한은 어떤 변수(n)가 특정 값(a)에 가까워지는 걸 말합니다.
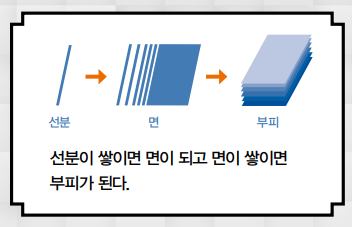
책을 예로 들어 보죠. 책은 얇은 종이로 이뤄져 있는데요, 종이 한 장의 옆면은 선분과 같습니다. 그 선분들이 쌓이면서 면이 생겨 책의 옆면이 되죠. 마찬가지로 밑변의 길이가 0에 가까운 직사각형을 선분이라고 생각하고 선분들을 합치면 전체 도형의 정확한 넓이을 구할 수 있어요. 이 개념은 나아가 적분으로 발전한답니다!
리만, 적분을 정의하다
그럼 적분은 무엇일까요? 그 이름도 유명한 독일 수학자 베른하르트 리만은 구분구적법과 극한을 활용해 ‘적분’을 엄밀하게 정의했어요. 적분은 구분구적법으로 함수의 넓이를 계산할 수 있도록 수식화한 방법으로, 함수의 그래프를 그렸을 때 끊어지는 부분이 없다면 특정 구간에서 그래프와 x축이 만드는 영역의 넓이를 구할 수 있죠. 이때 리만은 상한과 하한이라는 개념을 사용했습니다.
그림①을 보면 그래프 안쪽으로 만든 직사각형과 바깥쪽으로 만들어진 직사각형이 있어요. 안쪽 직사각형들의 넓이를 더한 것을 ‘리만 하한’ 바깥쪽 직사각형들의 넓이를 더한 것을 ‘리만 상한’이라고 부릅니다. 그림①을 보면 리만 상한이 리만 하한보다 크고 실제 정확한 넓이는 그 사이에 있겠죠? 직사각형의 밑변이 0에 가까울수록 두 값이 원래 넓이에 가까워지는 겁니다!
에고, 마크로 건물 하나 만들고 수학에 대한 설명이 구구절절 길었네요. 앞으로 여러분이 마크할 땐 수학동아 ‘퓨처TV’를 펴고 당당하게 외치세요. ‘엄마, 나 수학 공부 중이야!’