d라이브러리

어떻게 하면 수익을 최대화할 수 있을까? 지출을 최소화할 방법은 없을까? 최댓값과 최솟값을 구하는 문제는 실생활에 많이 쓰여요. 그중에서도 이차함수의 최댓값과 최솟값을 구하는 문제는 기본이라고 할 수 있죠. 이차함수를 그래프로 나타내 최댓값과 최솟값을 구해봅시다.

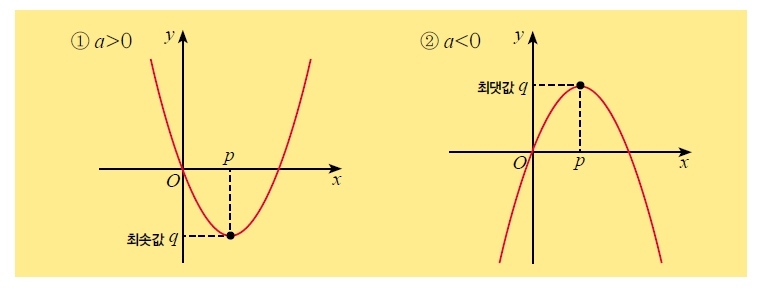
이차함수에서 y가 가질 수 있는 가장 작은 값과 큰 값은 어떻게 구할까요? 이차함수 y=ax²+bx+c를 y=a(x-p)²+q의 꼴로 고쳐서 a의 부호에 따른 그래프의 모양과 함숫값의 범위를 이용해 이차함수의 최댓값과 최솟값을 구할 수 있습니다.

① a＞0인 경우 그래프의 모양은 아래로 볼록합니다. 함숫값의 범위는 y≥q이므로 x=p일 때 최솟값은 q이고, 최댓값은 없습니다.
② a＜0인 경우 그래프의 모양은 위로 볼록합니다. 함숫값의 범위는 y≤q이므로 x=p일때 최댓값은 q이고, 최솟값은 없습니다.

이를 이용해 다양한 최대 최소 문제를 해결해 봅시다.

예제1. 관객이 400명 들어갈 수 있는 영화관에서 입장권을 10,000원에 팔면 180명의 관객이 입장합니다. 입장권의 가격을 500원 내릴 때마다 관객이 30명씩 더 온다고 할 때, 입장권의 가격을 얼마로 하면 수익이 최대가 되는지 구하세요.

풀이

(수익)=(입장권의 가격)×(관객수)로 계산할 수 있습니다. 입장권의 가격을 500x원 내리면 사람이 30x명 더 오므로 수입 y원에 대해 다음과 같은 식을 세울 수 있습니다.

y=(10000-500x)(180+30x)=-15000x²+210000x+1800000=-15000(x²-14x-120)

=-15000(x-7)²+2535000

-15000＜0이므로 이차함수 y=-15000(x-7)²+2535000의 그래프는 위로 볼록하고 x=7일 때 y=2535000으로 최대입니다. 따라서 입장권 가격이 10000-500X7=6500원일 때 수익이 2,535,000원으로 최대입니다.

도전문제1. 어느 도시의 2019년 1월 1일 인구는 110,000명이었습니다. 오랜 기간의 인구조사를 바탕으로 통계를 내보니 x년 전 이 도시의 인구를 y명이라고 할 때, x와 y 사이에는y=1000(0.25x²-4x+100)의 관계가 성립했습니다. 이 도시의 인구수가 최소인 해와 그때의 인구수를 구하세요.

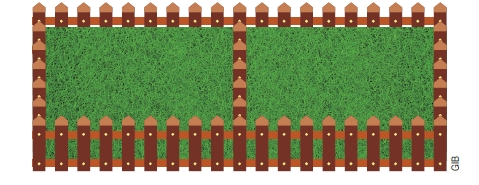
도전문제2. 아래와 같이 울타리를 만들어 직사각형 모양의 화단을 만들고, 가운데에 울타리를 세워 좌우의 넓이가 같게 하려고 합니다. 쓸 수 있는 울타리의 길이가 총 48m일 때, 화단의 최대 넓이를 구하세요.

(서술형 완전정복의 도전문제 정답 및 풀이는 2019년 12월 1일 수학동아 블로그에서 확인하세요.mathdonga.blog.me)