d라이브러리

▲미국 인기시트콤 '빅뱅이론'에서 73이 최고의 수라고 믿는 쉘던은 종종 73이 적힌 티셔츠를 입는다. Michael Yarish / 2019 Warner Bros. Entertainment Inc.

2007년 9월부터 2019년 5월까지 미국 CBS에서 방영한 인기 시트콤 '빅뱅이론'은 과학밖에 모르는 너드(Nerd·공부 외에는 별재주가 없는 엉뚱한 사람)  4인방과 매력적인 배우 지망생 페니 사이에 일어나는 에피소드를 그린 시트콤입니다. 

4인방 중 천재면서 괴짜인 쉘던 쿠퍼는 73화에서 “73은 21번째 소수고, 73을 뒤집은 37은 21을 뒤집은 12번째 소수야. 그리고 7과 3을 곱하면 21이지”라며 73을 ‘최고의 수’라고 말합니다. 
보통은 특이하다고만 생각했겠지만, 한 수학자는 달랐습니다. 2014년 이 에피소드를 본 크리스 스파이서 미국 모닝사이드대 수학과 교수는 73처럼 뒤집어도 소수고 원래 수의 소수 순번을 뒤집었을 때 뒤집은 수의 소수 순번이 나오는 소수를 ‘쉘던 소수’라 칭하고, 이런 수는 73밖에 없다고 예상했습니다. 일명 ‘쉘던의 추측’인데 2015년 미국 수학 잡지 ‘매스 호라이즌’에 이 내용을 소개했습니다.

▲'빅뱅이론' 포스터와 쉘던의 추측을 소개한 '매스 호라이즌'

매스 호라이즌을 본 칼 포머런스 미국 다트머스대 수학과 명예교수는 스파이서 교수에게 쉘던의 추측을 증명하자고 제안했습니다. 두 수학자는 각종 소수 관련 이론을 이용해 자연수 중 쉘던 소수의 후보를 유한개로 줄인 뒤 컴퓨터로 일일이 확인했습니다. 그리고 2019년 2월 미국수학회에서 만드는 학술지 ‘월간 미국 수학’에 쉘던의 추측을 증명한 논문을 발표합니다.

이 증명을 본 빅뱅이론의 과학 자문 담당 데이비드 잘츠버그 미국 캘리포니아대 물리학과 교수는 2019년 4월 18일 방영한 빅뱅이론 274화에 증명 일부를 화이트보드에 적어 등장시켰습니다. 소식을 들은 스파이서 교수는 가족들과 이 장면을 돌려봤다고 합니다.

각본 쓰다가 증명한 수학정리 

▲프라이는 외눈박이 릴라, 로봇 벤더와 함께 30세기의 미래를 헤쳐나간다. Everett

각본을 쓰기 위해 수학 문제를 직접 만들고 증명한 사람도 있습니다. 주인공은 1999년부터 2013년까지 방영한 미국 인기 애니메이션 ‘퓨처라마’의 작가 중 한 명인 켄 킬러입니다. 퓨처라마는 3000년 동안 냉동 기계에 들어갔다 깨어난 주인공 프라이가 미래에서 겪는 이야기를 그린 애니메이션입니다.

킬러는 퓨처라마 에피소드로 이런 줄거리를 떠올립니다. 

'등장인물 8명이 각자의 목적을 이루기 위해  ‘영혼을 바꾸는 기계’를 써서 몸을 바꾸는데, 한 번 영혼을 바꾼 두 사람은 다시 영혼을 바꿀 수 없어 위기에 빠진다.'

발상은 신선했지만, 마지막에 모든 영혼을 원래대로 돌려놓을 수 있는 건지 궁금했습니다. 미국 하버드대학교에서 응용수학으로 박사 학위를 받은 킬러는 이 내용을 수학 문제로 바꿔 해결했습니다. 군론을 이용해 ‘n명의 영혼이 뒤죽박죽 바뀌었을 때 영혼을 한 번도 바꾸지 않은 2명을 추가해 n명의 영혼을 원래대로 돌릴 수 있다’는 사실을 증명한 것입니다. 군론은 특별한 성질을 만족하는 집합인 ‘군’을 이용해 어떤 물체나 공간의 대칭성을 연구하는 대수학 이론입니다.

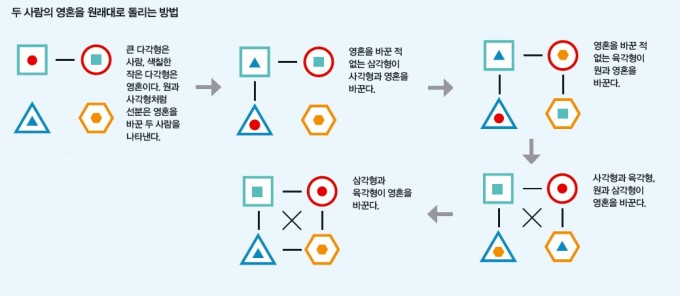
실제로 애니메이션에서는 영혼을 바꾼 적 없는 두 농구 선수가 칠판에 증명을 적은 뒤 8명의 영혼을 원래대로 바꿉니다. 이후 이 정리는 수학자들 사이에서 ‘퓨처라마 정리’, ‘킬러의 정리’라고 불리게 됐습니다. 작가가 되려면 수학도 잘 해야 하나봅니다.

익명의 덕후는 수학 천재?

▲스즈미야 하루히 시리즈는 2006년 방영한 일본 애니메이션으로 방송순서가 원작과 달라 화제였다. IMDB

2011년 미국의 커뮤니티 ‘4chan’의 한 게시판에 ‘스즈미야 하루히 14편을 모든 순서로 보려면 최소 몇 편을 봐야할까? 단, 겹쳐도 상관없다’는 질문이 올라왔습니다. 

질문을 이해하기 위해 1, 2, 3편으로만 생각해보겠습니다. 1, 2, 3편을 보는 순서 조합은 1-2-3, 2-3-1, 3-1-2, 2-1-3, 1-3-2, 3-2-1로 총 3!(=3×2×1)가지입니다. 모든 순서 조합을 보려면 18편을 봐야 한다는 얘기는 아닙니다. 1-2-3-1-2-1-3-2-1 순서로 9편만 보면 이 안에 6가지 순서 조합이 모두 포함돼 있습니다.

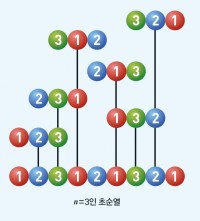
즉 모든 순서 조합을 포함하는 가장 짧은 배열이 무엇이냐는 질문입니다. 사실 이건 ‘초순열’을 찾는 오래된 수학 문제입니다. 초순열은 ‘문자 n개로 만든 순열을 모두 포함하는 길이가 가장 짧은 문자열’로, n이 6만 돼도 초순열의 길이가 800자리에 가까워 계산하기 어렵기 때문에 우선 길이의 하한과 상한을 찾아야 합니다.

2018년까지 수학자들은 문자가 n개면 초순열의 상한의 최솟값이 n!+(n-1)!+(n-2)!+…+1, 하한의 최댓값은 n!+(n-1)!로 알고 있었습니다. 그런데 영국 수학자 로빈 허스턴은 한 익명의 유저가 이 n!+(n-1)! 보다 더 큰 하한 n!+(n-1)!+(n-2)!+n-3을 찾아 증명했다는 걸 게시판 질문의 댓글에서 발견합니다. 하한은 초순열 길이의 최솟값을 뜻하므로 값이 클수록 초순열의 실제 길이에 가깝습니다.

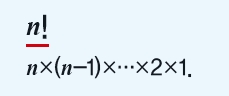
허스턴은 이 내용을 잘 정리해서 각종 수열을 사전처럼 찾기 쉽게 정리해 놓은 온라인 홈페이지 OEIS에 공개했습니다. 시트콤에서 애니메이션까지, 수학은 언제 어디서 튀어나올지 모릅니다. TV를 볼 때도 눈을 부릅뜨고 찾아보세요.