d라이브러리

따끈따끈한 피자 조각, 깊은 바닷속 산호초, 여러 종류의 나뭇잎…. 이들의 공통점은 뭘까요? 바로 쌍곡기하학의 예시라는 점입니다. 단순한 평면으로 나타낸 유클리드 기하학 대신 피자 도우 같은 얇은 면이 구부러지면서 나타내는 신기한 쌍곡기하학의 세계를 만나봅시다. 

우리 주변에서 가장 쉽게 볼 수 있는 도형은 무엇일까요? 빌딩, 책상, 모니터, 공책…. 인간이 만든 대부분의 물체는 직선으로 되어 있어요. 하지만 자연에서는 오히려 직선을 찾아보기 힘들어요. 동물, 식물 등 살아있는 생물의 표면은 거의 곡선의 형태를 띠거든요. 

그렇다면 왜 자연은 여러 형태 중 특히 주름진 표면을 많이 나타내는 걸까요? 주름진 표면으로 형성된 이유를 안다면 그 원리를 기계나 로봇 같은 인공물에도 적용할 수 있겠죠? 최근 미국의 한 수학자가 그 비밀을 밝혀냈어요. 어떤 내용인지 살펴보기 위해 먼저 얇은 물체의 기하학적 특성을 설명해 드릴게요. 자, 기하학이라고 하면 어려워할 사람도 누구나 맞힐 수 있는 문제를 내 보겠습니다. 준비되셨나요?

피자와 가우스 곡률

따끈따끈한 피자 한 판이 눈앞에 있어요. 그중 가장 토핑이 많고 맛있어 보이는 조각의 끝부분을 잡고 들어올립니다. 주우욱 늘어난 치즈에 침이 꿀꺽! 앗, 그런데 피자가 늘어지고 있어요. 너무 토핑을 많이 올렸는지 치즈와 함께 토핑이 와르르 떨어지려고 하는데 어떻게 해야 하죠?

이런 상황의 대처법은 모두 잘 알고 있을 거예요. 피자를 살짝 접으면 구부러졌던 피자 앞 부분이 똑바로 펴진다는 걸 말이죠. 누가 가르쳐주지 않아도 우리가 자연스럽게 했던 이런 행동이 바로 얇은 물체의 가장 기본적인 특성을 잘 보여줍니다. 

피자 도우나 비닐봉지 같은 얇은 물체의 한쪽을 잡고 든다고 할 때, 구부러지는 것은 아주 쉬운 반면 꼿꼿하게 펴기는 매우 어려워요. 그런데 구부러짐과 펼쳐짐은 서로 독립적인 요소가 아니기 때문에 어느 한 쪽을 조절함으로써 다른 쪽에 영향을 미칠 수 있어요. 이런 현상을 설명하는 것이 독일 수학자 카를 프리드리히 가우스의 ‘빼어난 정리’예요.  

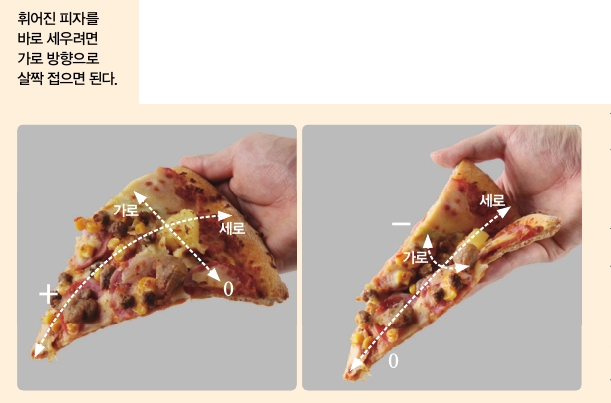
빼어난 정리는 ‘곡면을 찢지만 않으면 구부리거나 늘려도 가우스 곡률은 변하지 않는다’는 이론이에요. 여기서 가우스 곡률은 평면 위의 한 점에서 피자 도우가 얼마나 구부러졌는지 나타내는 수치랍니다. 피자에서의 가우스 곡률은 가로 방향의 곡률과 세로 방향의 곡률을 곱해서 구할 수 있어요. 아무 힘도 가하지 않은 평평한 상태의 피자는 구부러져 있지 않으므로 가우스 곡률이 0이에요. 빼어난 정리에 따르면 피자를 들었을 때도 가우스 곡률은 0이 돼야겠죠? 

아래 그림과 같이 피자 끝을 잡고 들어 올리면 가로 방향은 평평하니까 곡률이 0이에요. 그럼 가로×세로에서 이미 0이 들어갔으니 세로 곡률이 무엇이든 곱셈의 결과는 0이겠죠. 따라서 피자는 제멋대로 휘게 돼요. 이때 우리가 그래왔던 것처럼 양쪽을 접어 가로 방향으로 살짝 곡률의 크기를 늘리면 피자는 빼어난 정리에 따라 가우스 곡률 0을 유지하기 위해 세로 곡률이 0이 돼요. 그래서 피자 조각을 접으면 도우가 구부러지지 않게 되는 거죠.

  
모양 바꾸기 쉬운 주름진 쌍곡면

가우스 곡률을 이해했다면 이제 주름진 표면의 에너지 효율에 대해 알아보겠습니다. 가우스 곡률을 이용하면 3차원에서 매끄러운 면(미분이 가능한 곡면)은 다음과 같이 분류할 수 있어요. 한 점에서 가우스 곡률이 양수(+)인 구 모양, 가우스 곡률이 0인 평평한 모양, 그리고 가우스 곡률이 음수(-)인 말 안장 모양이죠. 그러면 주름진 곡선 모양은 이중 어디에 속할까요?

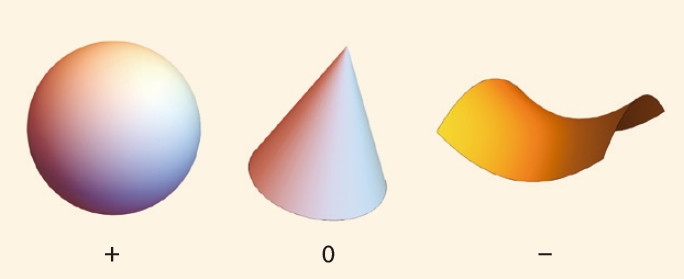
정답은 ‘어디에도 속하지 않는다’입니다. 오랫동안 학자들은 주름진 곡면이 마구 구겨놓은 종이와 비슷한 것이라고 생각해왔어요. 하지만 2019년 3월 미국 보스턴에서 열린 ‘미국물리학회’에서 수학자 샨카 벤카타라마니는 주름진 곡면은 가우스 곡률이 음수인 쌍곡면의 한 형태이면서 아주 독특한 개별적 특성을 지니고 있다는 사실을 발표했어요. 쌍곡면의 대표적인 형태인 말 안장 곡면은 모든 점에서 미분 가능한 표면을 지니고 있는 반면, 주름진 곡면은 미분이 불가능한 지점이 있으며 어느 점에서도 완전히 펼쳐지지 않은 표면을 지니고 있었던 거예요. 

매끄럽게 쫙 펼쳐진 물체를 구부리는 것보다 이미 어느 정도 구부러져 있는 물체를 구부리는 것이 훨씬 쉬우므로 어느 점에서도 완전히 펴진 형태가 아닌 주름 형태의 쌍곡면 표면은 적은 에너지로 모양을 바꾸기에 효율적인 구조였던 거예요. 이로써 많은 생물이 주름진 곡면을 가진 이유도 수학적으로 설명할 수 있게 됐죠.

벤카타라마니는 “수많은 물질과 시스템이 있지만 내가 아는 한 모두 에너지에 크게 좌우된다”며, 주름 모양의 곡면이 특별한 기하학적 특성을 갖고 있음을 설명했어요. 

간단한 피자 도우에서부터 유클리드 기하학을 넘어 쌍곡기하학까지 공부하는 동안 치즈가 푹 녹아내렸네요! 함께 꺼내 볼까요?

피자라는 한 글자만 보고 ‘이거다!’ 하고 달려들어 취재하기 시작한 기사였어요. 늘 수학보다 요리가 어려웠는데, 이번에는 수학이 피자 만들기보다 훨씬 어려웠습니다. 하지만 알면 알수록 신기하고 재미있어서 다시 한번 기하학의 매력을 느끼기도 했어요. 여러분도 그랬다면 좋겠네요! 

참고자료

Shankar Venkataramani ‘Elasticity, 
geometry, and sea-slugs’ 도움 샨카 벤카타라마니(아리조나대학교 수학과 교수)  디자인 유승민