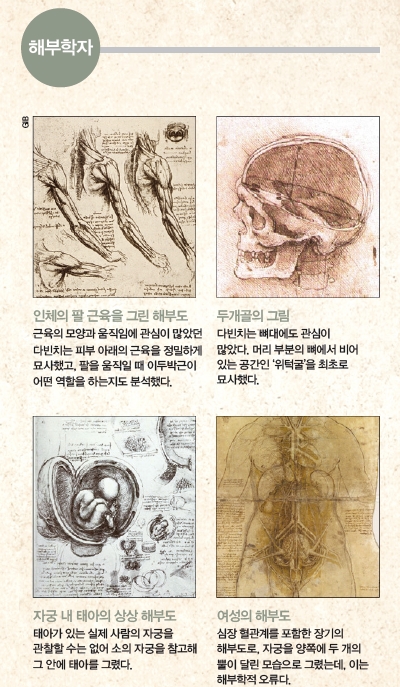
2019년 5월 2일은 레오나르도 다빈치가 세상을 떠난 지 500주기가 되는 날입니다. 다빈치 하면 모나리자 그림을 그린 화가, 비행기를 설계한 발명가…. 등이 떠오르죠? 다양한 분야에서 활약한 탓에 많이 알려지지 않은 모습이 하나 더 있습니다. 바로 수학자 다빈치입니다. 그의 발자취를 따라가 보며 수학자의 면모도 만나봅시다.
증거① 원의 구원 문제에 도전했다!

다빈치는 원 하나를 그리고 그 원과 넓이가 똑같은 정사각형을 작도하는 문제에 관심을 가졌습니다. 문제를 풀기 위해서는 먼저 원의 면적을 구해야 했는데, 방정식을 다룰 수 없던 다빈치는 원을 삼각형 또는 사각형으로 쪼개 보기도 하고, 원의 둘레를 펼쳐 길이를 측정하기도 했습니다. 10여 년간 수많은 시도를 했지만, 결국 문제 해결에는 실패합니다.
사실 이 문제는 ‘원의 구적 문제’라 불리는 고대 그리스 시절부터의 난제로, 19세기 들어 독일 수학자 페르디난트 폰 린데만이 원의 넓이와 같은 정사각형을 작도할 수 없다는 것을 밝힙니다. 원의 넓이를 구할 때 필요한 원주율이 초월수, 즉 작도가 불가능한 수였기 때문입니다.
다빈치는 죽음을 앞두고 쓴 노트의 마지막 페이지에서도 면적은 같지만, 밑변과 높이가 다른 네 개의 직각삼각형을 작도하는 문제를 풀었습니다. 이 연구는 “수프가 식고 있다…”라는 말로 끝났지만, 다빈치가 평생 기하학 문제를 고민한 것을 확인할 수 있습니다.
증거② 수학책에 입체도형을 그렸다!

1482년, 다빈치는 밀라노로 가서 당시 밀라노의 통치자였던 루도비코 스포르차 공작의 궁정에 들어갔습니다. 그곳에서 수학자 루카 파치올리를 만납니다. 이후 파치올리에게 유클리드 기하학과 제곱, 제곱근의 곱셈을 배웁니다. 그 보답으로 1496년에는 파치올리가 쓴 수학책 ‘신성한 비례’에 실릴 입체도형을 그렸죠. 신성한 비례는 황금비를 다양한 입체도형에서 찾을 수 있다는 내용을 담은 책이었습니다. 다빈치는 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체와 구, 원뿔, 원기둥, 피라미드 등의 입체도형들을 그렸는데, 특히 구조를 명확히 보여주기 위해 입체도형을 겨냥도로 나타내기도 했습니다. 기하학에 대한 관심과 연구가 없었다면 그리기 어려웠을 이 도형들은 다빈치 생전에 출간된 유일한 그림입니다.
파치올리는 책 서문에서 “형언할 수 없을 만큼뛰어난 왼손잡이이자 모든 수학 분야에 정통한 인물”인 다빈치가 고맙게도 삽화를 그려줬다고 소개하기도 했습니다.
증거③ 사면체의 무게중심을 발견했다?
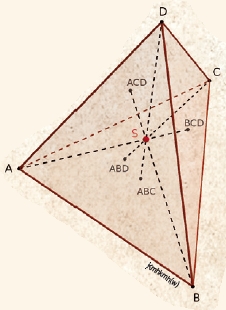
다빈치는 도형에 대한 깊은 고찰로 사면체의 무게중심을 발견했습니다. 사면체의 꼭짓점에서 마주 보는 면의 무게중심을 잇는 선분을 모두 그리면 한 점에서 만나고 이 점은 각 선분을 3:1로 내분하는데, 다빈치가 남긴 노트에 이 내용이 있었던 겁니다. 하지만 이 점을 발견했다는 내용만 있을 뿐 수학적으로 증명하거나 찾는 과정은 남겨져 있지 않았습니다. 아쉽게도 다빈치가 세상을 떠난 이후인 1565년에 수학적으로 이를 증명한 이탈리아의 수학자 페데리코 콤만디노의 이름을 따 콤만디노의 정리로 이름 붙여졌습니다.
살아생전에 다빈치는 “수학이 적용되지 않는 과학에는 확실성이 없다”라고 말할 정도로 수학에 대한 애정을 드러냈습니다. 지식의 한계로 다양한 수학을 다루지는 못했지만, 누구보다 열정적으로 기하학 연구에 몰두했죠. 어떤가요? 이 정도라면 다빈치를 수학자로 기억해도 되지 않을까요?