도넛과 손잡이가 하나인 컵이 위상수학적으로 같다는 말 들어보셨나요? 찰흙으로 도넛 모양을 만든 다음 칼로 자르거나 구멍 내지 않고 조물조물 만지면 손잡이가 하나인 컵 모양을 만들 수 있어 위상수학적으로 같다고 합니다. 같은 원리로 구와 모든 다면체도 위상수학적으로 같은데요, 최근 이와 관련된 문제에서 새로운 결과가 나왔습니다.
3차원에 속이 비어 있는 공이 하나 있습니다. 이 공을 누르거나 당겨서 다른 모양을 만들려고 합니다. 절대 찢으면 안 되고, 공 위의 한 점이 다른 점에 붙어서도 안 됩니다. 이 방법으로 다양한 모양을 만들 수 있는데요, 특히 위상수학자들은 공의 구부러진 표면을 반듯하게 펴서 삼각형을 만든 뒤 삼각형끼리 붙여서 만든 도형으로 연구를 많이 합니다. 즉 모든 면이 삼각형인 다면체를 대상으로 연구하는 거지요.
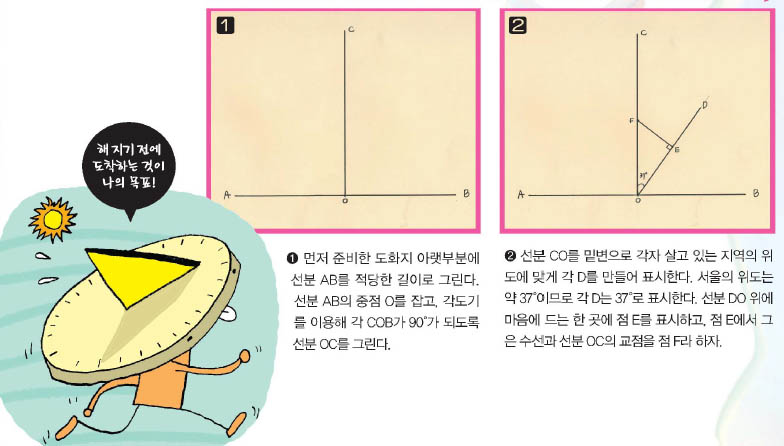
이렇게 만든 다면체의 한 예로 4개의 꼭짓점으로 만들 수 있는 정사면체가 있습니다. 정사면체에는 꼭짓점이 4개, 변이 6개, 면이 4개가 있어 오일러 지표가 꼭짓점의 수-변의 수+면의 수=4-6+4=2입니다. 또 다른 경우로 꼭짓점 6개로 만들 수 있는 정팔면체가 있습니다. 정팔면체에는 꼭짓점이 6개, 변이 12개, 면이 8개가 있어, 이 역시 오일러 지표가 6-12+8=2입니다.
1752년 스위스 수학자 레온하르트 오일러가 증명한 오일러 다면체 정리에 의하면 이런 다면체의 오일러 지표는 항상 (꼭짓점의 수)-(변의 수)+(면의 수)=2입니다. 꼭짓점은 0차원, 변은 1차원, 면은 2차원이니 꼭짓점의 수를 f0, 변의 수를 f1, 면의 수를 f2라고 쓴다면 3차원에 있는 공을 변형해 얻은 다면체는 항상 f0-f1+f2=2이지요.
사실 이런 일이 3차원에서만 일어나는 것은 아닙니다. 4차원은 상상하기 어려우니 먼저 2차원을 생각해봅시다. 2차원 공간은 평면입니다. 평면에서 ‘구’란 한 점에서 같은 거리만큼 떨어진 점의 모임일 테니 우리가 알고 있는 원입니다. 원을 구부려서 만든 ‘다면체’란 결국 우리가 잘 아는 다각형이 됩니다.
삼각형도 그 한 예입니다. 삼각형의 꼭짓점의 수는 3개, 변의 수는 3개입니다. 사각형이라면 꼭짓점이 4개, 변이 4개겠죠? 일반적으로 2차원 원을 구부려서 얻은 다면체에서 꼭짓점의 수가 f0, 변의 수가 f1이라고 하면, 이 두 수는 항상 같을 수밖에 없습니다. 따라서 f0-f1=0입니다.
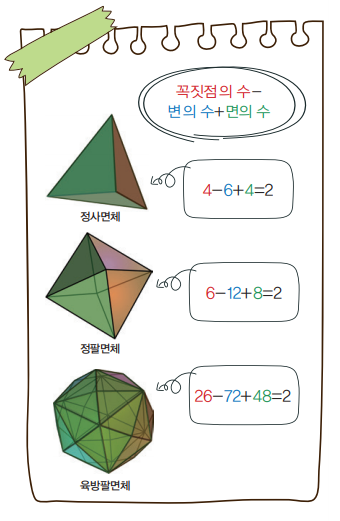
1차원에서는 어떤가요? 1차원 공간은 직선입니다. 1차원에 사는 사람이 ‘구’를 떠올린다면, 한 점에서 같은 거리만큼 떨어진 점들의 모임이므로 그 직선 위에 있는 두 점으로 이뤄집니다. 따라서 꼭짓점의 수 f0은 2개로 2입니다.
4차원 단체 구 만들기
이제 4차원 공간을 상상해 봅시다. 4차원 공간의 ‘구’ 역시 한 점에서 같은 거리 떨어진 점들로 이뤄집니다. 이 구를 잘 움직이고 구부리고 나눠 다면체로 만들어봅시다. 이때 모든 ‘조각’을 가장 ‘단순한’ 형태로만 생각합시다. 즉 모든 ‘2차원 면’은 삼각형, 모든 ‘3차원 면’은 사면체라고 여깁시다. 이런 면들을 잘 조합해 구와 위상수학적으로 같은 도형을 만드는 방법은 무한히 많은데요, 이를 단체 구(simplicial sphere)라고 부릅시다. 그리고 f0을 0차원인 꼭짓점의 수, f1을 1차원인 변의 수, f2를 2차원인 삼각형의 수, f3을 3차원인 사면체의 수라고 해봅시다.
가장 간단한 4차원 단체 구에는 어떤 것이 있을까요? 우선 4차원에서 점 5개가 이루는 1차원 선분은 점 5개 중의 2개를 뽑는 경우의 수이므로 5×4÷2=10개입니다. 이 점 5개로 만들 수 있는 2차원 삼각형 면은 점 5개 중의 3개를 뽑는 경우의 수로 (5×4×3)÷(3×2×1)=10개지요. 마찬가지 방법으로 이 점 5개로 만들 수 있는 3차원 사면체 면은 (5×4×3×2)÷(4×3×2×1)=5개입니다. 따라서 f0=5, f1=10, f2=10, f3=5가 되고, f0-f1+ f2-f3=0입니다.
한편 4차원에서 만들 수 있는 단체 구는 위상수학적으로 같은 것을 하나로 치더라도 무한히 많지만, 항상 f0-f1+f2-f3=0이라는 것이 알려져 있습니다. 심지어 n차원에서도 비슷한 방식으로 단체 구를 만들면 f0-f1+f2-f3+…+(-1)n-1fn-1 의 값이 n이 홀수면 2, n이 짝수면 0입니다. 프랑스 수학자 앙리 푸앵카레가 대수적 위상수학 방법을 써서 이걸 증명했지요. 이처럼 단체 구에서 얻을 수 있는 f 값들은 특정 수로 정해져 있습니다. 이 f 값들을 모은 (f0, f1, f2, …, fn-1)을 흔히 ‘f-벡터’라고 부르지요.
f-벡터가 될 수 있는 값은?
다시 3차원으로 내려가 봅시다. 3차원 단체 구라고 하면 모든 면이 삼각형으로 나눠진 구가 되겠지요. 이때 각각의 변은 정확하게 2개의 삼각형 면과 만나야 하니 2f1=3f2라는 식이 얻어집니다. 이를 오일러 지표 공식 f0-f1+f2=2에 대입하면 f1=3f0-6이라는 식이 나오지요. 즉 n개 꼭짓점으로 만들어진 단체 구의 변의 수는 정확히 3n-6개고, 3차원의 단체 구에서 만들 수 있는 f-벡터는 (n, 3n-6, n)밖에 없습니다.
1970년 영국의 수학자 피터 맥뮬렌은 n차원 공간에 있는 단체 구가 가질 수 있는 모든 f-벡터가 어떤 값들인지 알 수 있는 추측을 제시합니다. 이 추측을 흔히 ‘g-추측’이라고 부릅니다. 단체 구 중에 좀 쉬운 것들, 즉 n차원 볼록다면체의 겉면으로 나타나는 단체 구에 대해 1981년 루이스 빌레라와 칼 리가 쓴 논문과 1980년 리처드 스탠리가 쓴 논문 결과로 이미 가능한 모든 f-벡터가 어떤 값인지 완전히 밝혀졌습니다.
20세기 초반 수학자들은 3차원에서는 속이 꽉 찬 다면체에서 겉면만 이용하면 모든 가능한 단체 구와 같은 모양을 만들 수 있다는 것을 증명합니다. 하지만 4차원에서는 그런 식으로는 만들 수 없는 단체 구가 있었습니다. 즉 g-추측의 특수한 경우는 이미 해결했지만, 일반적인 단체 구에 대해서는 문제를 풀지 못한 것이죠. 이 문제는 한참 동안 미해결로 남아 있었습니다.

그런데 2018년 12월 26일 독일 출신 젊은 수학자 카림 아디프라지토 이스라엘 예루살렘 히브리대학교 교수가 g-추측을 해결했다고 주장하는 논문을 인터넷 논문 공개 사이트인 ‘아카이브’에 올렸습니다. 이 논문에는 맥뮬렌의 g-추측보다 더 강력한 성질의 증명이 담겨 있습니다. 이 결과를 쓰면 르네 데카르트와 오일러의 결과를 확장하는 ‘그륀바움-칼라이-사르카리아의 추측’ 또한 증명됩니다.

아디프라지토 교수는 미국 고등과학연구소에서 연구하는 허준이 박사와 공동연구한 업적으로 2019년 브레이크스루 뉴호라이즌상을 허 박사와 함께 받았습니다. 2018년에 허 박사가 g-추측에 관해 영어로 설명하는 동영상이 유튜브에 올라온 것이 있으니 참고하셔도 좋겠습니다. 앞으로 검증에 조금 시간이 걸리겠지만, 만일 이 증명이 옳다면, 수백 년간 수학자들이 연구해오던 다면체가 갖는 성질을 하나 더 깊게 이해하게 됩니다. 이렇게 단순해 보이는 대상에 수많은 대칭성의 비밀이 숨어있으니 정말 신비롭지 않나요?