d라이브러리

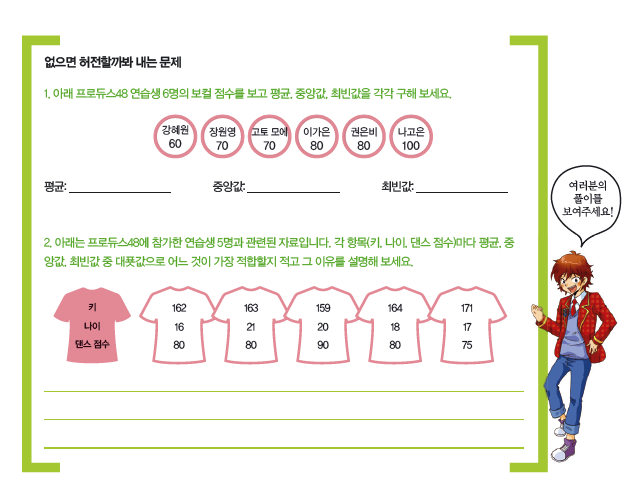
BJ맹추는 요즘 ‘프로듀스48’에 푹 빠져 있습니다. 제가 선호하는 연습생을 데뷔시키기 위해 폭풍 투표를 하고 있지요. 기왕이면 데뷔도 하고 센터도 하면 참 좋을 텐데…. 음? 센터는 무조건 외모가 뛰어나야 한다고요? 그건 생각하기 나름이랍니다!

그때그때 다른 ‘센터’

팀에서 주목을 가장 많이 받는 센터! 가운데 서서 카메라를 한 몸에 받으니 인지도 올리기도 쉽고 인기도 얻을 수 있어서 누구나 탐내는 자리가 바로 센터입니다. 동시에 그룹을 대표해야 해서 부담스러운 자리기도 하지요.

여러분이 생각하기에 센터가 갖춰야 할 자질은 무엇인가요? 가수니까 기막히게 노래를 잘하거나 춤을 잘 추는 것? 아니면 비주얼이 가장 뛰어난 것? 딱히 정답이 있는 건 아닙니다. 노래, 춤, 비주얼 모두 팀을 대표할 수 있는 요소니까요.

실제로 방송을 보면 같은 팀에서도 어떤 노래에 맞춰 공연하냐에 따라 센터를 바꿉니다. 가창력이 필요한 노래를 할 때는 노래를 잘하는 멤버가, 신나고 깜찍한 노래를 할 때는 귀엽고 상큼한 외모를 가진 멤버가 센터가 될 확률이 높습니다. 

꼭 아이돌 그룹이 아니어도 이건 명심하세요. 센터 같은 ‘대표’를 정할 때 ‘무엇을 대표하느냐’에 따라 그에 맞는 대표를 뽑아야 해요!

자료의 대표를 뽑아라! 

아이돌 그룹에만 대표가 필요한 건 아닙니다. 반을 대표하는 반장, 학교를 대표하는 교장 선생님, 축구팀을 대표하는 주장처럼 여러 사람이 모인 곳엔 늘 대표가 필요하지요. 

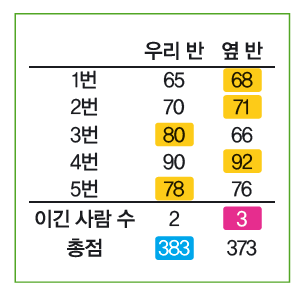
수치로 이뤄진 통계 자료도 예외는 아닙니다. 자료를 대표하는 수치가 필요한 상황이 반드시 있거든요. 예를 들어 시청자 여러분이 학생 수가 30명인 반의 담임선생님이고 학생들의 수학 점수를 조사했다고 생각해 보세요. 우리 반이 옆 반보다 수학 시험을 더 잘 봤는지 알고 싶으면 어떻게 해야 할까요?

바로 떠오르는 방법은 각 반의 1~30번의 점수를 각각 비교해 점수가 높은 학생이 많으면 잘 본 걸로 하는 겁니다. 그런데 더 못 본 반의 담임선생님은 이렇게 얘기할 수 있겠죠. ‘총점은 우리 반이 더 크다!’고 말이에요.

담임선생님들끼리 서로 다투지 않게 하려면 이렇게 많은 자료의 크기를 비교할 수 있는 공평한 방법이 필요하겠죠? 이때 쓰는 게 바로 ‘대푯값’입니다. 낯선 용어가 나왔다고 걱정하지 마세요. 여러분은 이미 대푯값을 무척 많이 활용하고 있으니까요. 학교에서 시험을 볼 때마다 매번 계산하는 ‘평균’이 바로 대표적인 대푯값이거든요. 

평균은 자료의 값을 모두 더한 뒤 자료의 수로 나눈 값이에요. 자료 수가 같을 때 총점이 높으면 평균도 높고, 평균끼리 비교하면 수치 하나의 크기만 비교하면 되니까 간단하고 공평합니다.

피타고라스의 별난 평균

평균을 꼭 여러분이 아는 방법대로 구할 필요는 없습니다. 그리스 수학자 피타고라스가 만든 피타고라스 학파는 평균을 구하는 세 가지 방법을 찾아냈습니다. 나중에는 멋들어진 이름도 붙었죠.

우리가 알고 있는 평균은 ‘산술 평균’으로 자료 n개가 있을 때 자료의 값을 모두 더해서 n으로 나눈 값입니다. 두 번째는 ‘기하 평균’으로 자료의 값을 모두 곱한 뒤 그 값의 n제곱근을 구하는 것이고, 세 번째는 ‘조화 평균’으로 n을 각 자료의 역수의 합으로 나눈 값이예요.

세 평균은 모두 대푯값 역할에 적합하면서 동시에 부등식 ‘조화 평균≤기하 평균≤산술 평균’을 만족해서 흥미롭습니다!

여러 가지 대푯값

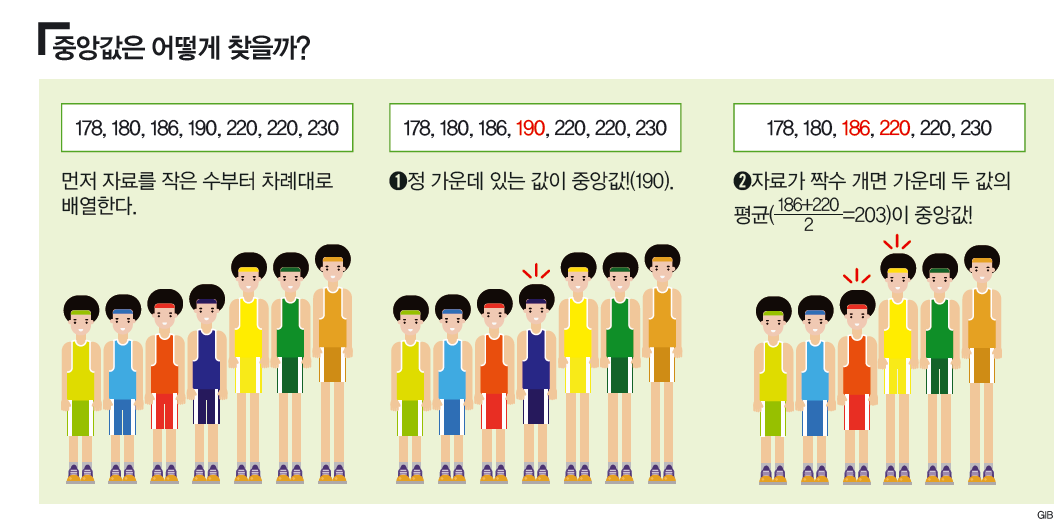
프로듀스48에서 노래에 따라 다른 센터를 뽑듯, 자료도 상황에 따라 평균이 아닌 다른 대푯값을 찾아야 할 때가 있습니다. 평균 다음으로 많이 쓰는 대푯값은 ‘중앙값’과 ‘최빈값’입니다. 이름에서 추측할 수 있듯이 중앙값은 자료를 크기순으로 나열했을 때 중앙에 있는 값, 최빈값은 가장 많이 등장한 값을 뜻합니다.

중앙값이 나서야 할 때는 자료의 크기 차이가 클 때입니다. 예를 들어 1, 2, 3, 4, 50의 평균을 구해보면 12가 나옵니다. 자료를 보지 못한 사람은 평균이 12니까 각 자료의 값이 대충 12와 비슷하다고 추측할 거예요. 그런데 실제 자료에서 12와 비슷한 값은 하나도 없습니다. 이때는 평균보다 중앙값(3)을 찾으면 자료를 더 정확하게 추측할 수 있지요.

이제 신발 가게 사장님이 됐다고 생각해 봅시다. 오늘 판 신발의 크기를 조사해보니 230, 245, 250, 250, 255, 250, 260, 270입니다. 많이 팔린 크기의 신발을 주문해야겠죠? 그러면 먼저 주문해야 할 크기는 자료에서 가장 많이 등장한 250입니다. 이때는 대푯값으로 최빈값을 선택하는 게 적절해요.

이런 경우엔 어떡할까?

더하고 나눠야 하는 평균보다 중앙값과 최빈값을 구하는 게 더 쉬워 보인다면 착각입니다. 계산은 덜 해도 구할 때 헷갈리는 경우가 많거든요. 

‘백문이불여일견’이니 몇 가지 자료를 직접 보는 게 좋을 것 같군요.

우선 1, 2, 3, 4, 5, 6처럼 자료의 수가 짝수인 경우 중앙에 아무 숫자도 없습니다. 이때는 중앙에 있는 두 수(3, 4)의 평균( 3+42 =3.5)을 중앙값으로 생각하면 됩니다. 그럼 최빈값은 무엇일까요? 각 자료가 똑같은 횟수만큼 등장하면 최빈값은 없습니다. 각 신발 크기가 모두 똑같이 팔렸으면 굳이 하나만 골라서 주문할 필요가 없지요.

1, 2, 2, 3, 3처럼 가장 많이 등장한 숫자가 두 개(2, 3)면 이때는 2와 3이 모두 최빈값입니다. 결국 최빈값은 경우에 따라 없을 수도 있고 무척 많을 수도 있는 거예요! 

대표는 늘 부담스럽다!

상황에 따라 대푯값을 무엇으로 할지 고르는 것도 중요하지만, 어떤 상황에서 대푯값을 골랐는지 아는 것도 중요합니다. 중앙값이 필요한 이유처럼, 평균을 보고 ‘모든 자료가 평균에 가깝다’고 추측하는 건 금물이지요.

현실에서도 비슷합니다. 누군가 대표를 맡았다고 해서 ‘모든 사람이 대표와 비슷할거야’라든가 ‘대표니까 모든 면에서 으뜸이겠지?’라고 생각하면 대표는 엄~청 부담스러울 거예요. 다짜고짜 엄격한 잣대를 들이대기보다 어떤 상황에서 대표로 뽑았는지 알면 좀 더 객관적으로 생각할 수 있을 겁니다. 그럼 오늘 배운 세 가지 대푯값을 잘 활용하길 바라면서 이만 물러갑니다! 뿅!