원의 넓이를 구하려면 원주율이 꼭 필요합니다. 왜 원의 크기와 관계없이 지름에 대한 원주의 비인 원주율은 일정할까요? 이 질문을 해결하기 위해 원의 넓이에 대해 함께 알아보도록 하겠습니다.

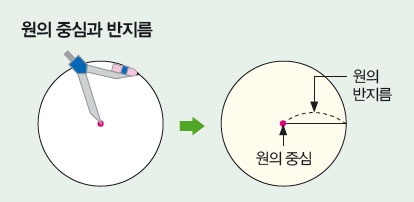
컴퍼스를 이용해서 한 끝점을 고정시키고 다른 한 끝점을 한 바퀴 돌려 나온 도형을 원이라고 합니다. 즉 한 점에서 일정한 거리에 있는 점들이 만든 도형을 원이라고 하는 것이지요. 컴퍼스로 찍은 점을 원의 중심, 원의 중심에서 원 위에 있는 한 점까지의 거리를 원의 반지름이라고 합니다. 한 원에서 반지름의 길이는 모두 같기 때문에 원 모양이 둥근 것이고, 바퀴나 굴렁쇠, 훌라후프가 잘 굴러가는 이유는 원의 중심에서 땅에 이르는 거리(반지름)가 일정하기 때문입니다.
따라서 원의 크기와 관계없이 지름에 대한 원주의 비인 원주율(=원의 둘레÷원의 지름)은 항상 일정합니다. 이 때문에 지름을 알면 원주를 알 수 있거나 원주를 알면 지름을 알 수 있습니다. 이렇게 항상 일정한 원주율은 유리수처럼 정확하게 떨어지는 수가 아니라서 3, 3.1 혹은 3.14를 사용합니다. 왜 그럴까요?


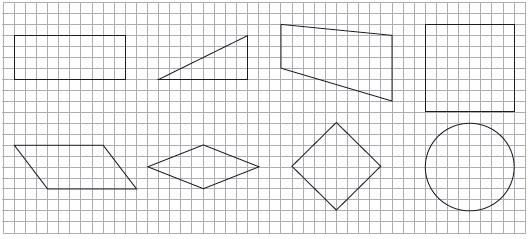
일본에서는 원의 넓이를 지도하기 전에 모눈종이 위에 도형을 보여주며 이미 배운 도형의 넓이를 구하게 합니다. 자연스럽게 원의 넓이를 어떻게 구하는지 생각해 보게 하는 것입니다. 다각형의 넓이는 쉽게 구할 수 있지만, 원의 넓이는 쉽게 구하지 못하기 때문에 적합한 동기유발 자료가 됩니다.
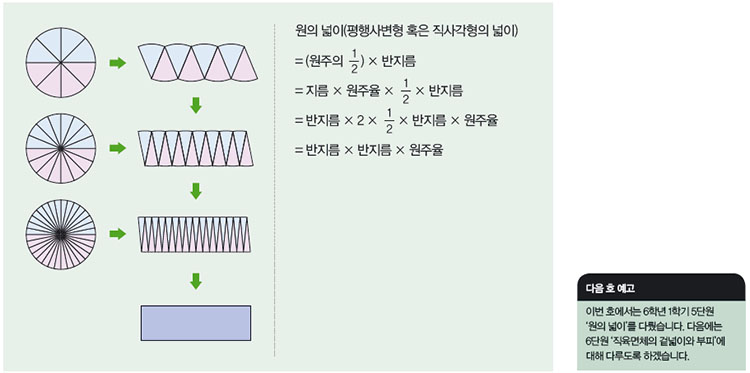
원의 넓이는 구분구적법을 활용해 구할 수 있습니다. 구분구적법이란 평면도형의 넓이나 입체의 부피를 구하기 위해 충분히 작은 n개의 기본 도형으로 세분하여, 그 도형의 넓이 또는 부피의 근삿값을 구하는 방법입니다. 다음은 원을 잘게 잘라 평행사변형이 직사각형이 될 때까지 한없이 잘라 붙여 원의 넓이를 구하는 구분구적법의 한 예입니다.